[离散时间信号处理学习笔记] 4. 线性常系数差分方程
本文主要从离散时间系统的角度来讨论线性常系数差分方程,不过其中也不可避免地涉及到数学方面的分析,因此在阅读本文章之前,如果对线性常系数差分方程在数学上有一定的认识,将更有助于理解本文的相关内容。
推荐阅读:
递推表示
累加器系统
这里从累加器来引入差分方程这一概念。
累加器系统定义为
$y[n] = \displaystyle{ \sum_{k=-\infty}^{n}x[k] }$
从上面定义的式子可以得到
$y[n-1] = \displaystyle{ \sum_{k=-\infty}^{n-1}x[k] }$
等号两边相减得到
$y[n]-y[n-1] = x[n]$
从累加器的定义上来说,当前输出与前一个输出的差值确实为当前的输入。换一个角度来说,当前的输出等于前一个输出与当前输入的和
$y[n] = y[n-1] + x[n]$
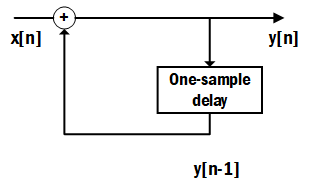
这种当前的值的计算会用到前面已算出的值的差分方程就是差分方程的递推表示(迭代法)。这种差分方程的递推表示使得系统实现更为简单,在离散时间系统的实现中经常用到。累加器系统的递推差分方程方框图如下表示
滑动平滑系统
滑动平滑系统的定义是
$y[n] = \displaystyle{ \frac{1}{M_1+M_2+1}\sum_{k=-M_1}^{M_2}x[n-k] }$
令$M_1=0$以使系统称为因果的。那么该系统的定义变为
$y[n] = \displaystyle{ \frac{1}{M_2+1}\sum_{k=0}^{M_2}x[n-k] }$
单位脉冲响应为
$h[n] = \frac{1}{M_2+1}(\delta[n] – \delta[n-M_2-1])*u[n] $
可以看到式子中分为三个部分:衰减器、样本延迟、累加器。表示成方框图如下
线性常系数差分方程
线性时不变系统中的一个重要的子系统是由这样一些系统组成,这些系统的输入$x[n]$和输出$y[n]$满足$N$阶线性常系数差分方程,其形式为
$\displaystyle{ \sum_{k=0}^{N}a_k y[n-k]=\sum_{m=0}^{M}b_m x[n-m] }$
线性常系数差分方程的求解
线性常系数差分方程的解可以分为两部分
$y[n] = y_p[n]+y_h[n]$
其中$y_p[n]$为特解,$y_h[n]$为齐次解,我们这里就齐次解简单展开说明。齐次解是假设$x[n]=0$时求得的$y[n]$,即有如下齐次差分方程
$\displaystyle{ \sum_{k=0}^{N}a_k y_h[n-k] } = 0$
在求解差分方程的过程中,我们会假设
$y_h[n] = Az^n$
然后代入上述齐次差分方程,整理后得到
$\displaystyle{ \sum_{k=0}^{N}a_k z^{-k} } = 0$
求解该方程后可以得到$N$个不同的$z$值都能满足上述方程(没有重根的情况下),即
$z_m,m=1,2,\cdot\cdot\cdot,N$
另外,无论$A_m$为什么值,在把$y_h[n] = A_m z_m^n$代入到齐次差分方程都能得到满足,因此$y_h[n]$的解为
$y_h[n] = \displaystyle{ \sum_{m=1}^{N}A_m z_m^n }$
此时$z_m$的值已知,$A_m$未知,那么此时就需要辅助条件来求解$A_m$,辅助条件可以由一些特定$n$点上的特定$y[n]$值组成,诸如$y[-1],y[-2],\cdot\cdot\cdot,y[-N]$,然后求解一组由N个线性方程构成的方程组来求得$N$个特定系数$A_m$。
线性常系数差分方程的迭代分析法
线性常系数差分方程在单独取出$y[n]$可以得到下面的等式
$y[n] = \displaystyle{ –\sum_{k=1}^{N}\frac{a_k}{a_0}y[n-k] + \sum_{k=0}^{M}\frac{b_k}{a_0}x[n-k] }$
如果对所有$n$的输入$x[n]$以及一组辅助值,如$y[-1],y[-2],\cdot\cdot\cdot,y[-N]$都给定的话,那么$y[0]$就能通过上面的式子求出,然后又能通过同样的方法求出$y[1]$,以此类推。最终能递推地得到任意$n$上的输出值$y[n]$。
初始松弛条件(initial-rest condition)
本书主要关心的是LTI系统,而满足因果性的LTI系统在未开始输入的情况下是不会有输出的。
证明:
LTI系统的定义为
$y[n] = \displaystyle{ \sum_{k=-\infty}^{\infty}x[k]h[n-k] }$
假设输入$x[n]$在点$n_0$开始进行输入,即$x[n]=0,n<n_0$,则
$y[n] = \displaystyle{ \sum_{k=n_0}^{\infty}x[k]h[n-k] }$
如果该系统是因果系统,即$h[n]=0,n<0$
$\begin{align*}
y[n] &=\left\{\begin{matrix}
\displaystyle{\sum_{k=n_0}^{\infty}x[k]h[n-k]}, &n-k\geqslant0 \\
0, &n-k<0
\end{matrix}\right. \\
&=\left\{\begin{matrix}
\displaystyle{\sum_{k=n_0}^{\infty}x[k]h[n-k]}, &n\geqslant k \\
0, &n<k
\end{matrix}\right. \\
&=\left\{\begin{matrix}
\displaystyle{\sum_{k=n_0}^{\infty}x[k]h[n-k]}, &n\geqslant k \\
0, & n_0\leqslant n<k\\
0, &n<n_0
\end{matrix}\right. \\
\end{align*}$
因此用于表征因果的LTI系统的线性差分方程也需要遵循这一条件,具体表现在辅助条件上
$if\ x[n]=0,\ n<n_0 \quad then \ y[n]=0,\ n<n_0 $
这一条件被称为初始松弛条件。
例如:
- 如果输入为单位跃阶序列,即$x[n] = u[n]$,也就是说$x[n]=0,n<0$。此时LTI系统则要求$y[n] = 0,n<0$。
- 如果输入序列为$x[n]=u[n-12]$,也就是说$x[n]=0,n<12$。此时LTI系统则要求$y[n]=0,n<12$。
有了初始松弛条件,就能依据该条件作为辅助条件求解线常系数性差分方程。
如果一个LTI系统是因果的,那么该系统就满足初始松弛条件;如果一个系统由线性常系数差分方程表征,并满足初始松弛条件,那么这就是一个满足因果性的LTI系统。
$Causal ,LTI \Leftrightarrow initial\ rest$