二阶线性差分方程中的根/特征值的讨论

二阶线性差分方程的齐次解/通解

以下面的二阶线性差分方程为例

$ay_{t+2}+by_{t+1}+cy_t = d$

我们在求该差分方程的齐次解（通解）时，会令等式右边等于0，得到二阶齐次线性差分方程：

$ay_{t+2}+by_{t+1}+cy_t = 0$

并假设

$y_t = A\omega^t$

把该假设代入上面齐次方程，整理后得到：

$a\omega^2+b\omega+c = 0$

这个一元二次方程的根为

$\omega = \frac{-b\pm\sqrt{b^2-4ac}}{2a}$

 

 

二阶线性差分方程中的根

$\omega$是该方程的根（characteristic root），又称为该方程的特征值（eigen value）。此时$\omega$可以分成三种情况讨论。

 

$b^2-4ac >0 $

此时$\omega$分别为两个不相同的实数

差分方程的齐次解为：

$y_h(t) = A_1\omega_1^t+A_2\omega_2^t$

 

$b^2-4ac = 0$

此时$\omega$为重根

差分方程的齐次解为：

$y_h(t) = (A_1n+A_2)\omega^t$

 

$b^2-4ac <0$

此时$\omega$分别为两个共轭复数

$\omega = -\frac{b}{2a} \pm \frac{\sqrt{b^2-4ac}}{2a} = h\pm iv$

即有：

$\left\{\begin{matrix}
h &= &-\frac{b}{2a} \\
v &= &\frac{\sqrt{4ac-b^2}}{2a}
\end{matrix}\right.$

差分方程的齐次解为：

$y_h(t) = A_1(h+iv)^t + A_2(h-iv)^t$

 

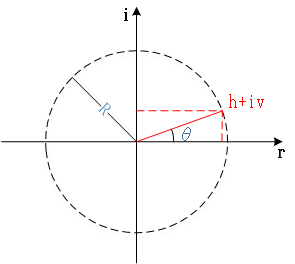
该共轭的根还可以从极坐标方面进行讨论

$h\pm iv = R(cos \theta \pm isin\theta)$

其中

$R = \sqrt{h^2+v^2} = \sqrt{\left| \frac{c}{a} \right|}$

即R是一个固定的实数。

 

差分方程的齐次解为

$\begin{align*}
y_h(t)
&= A_1R^t(cos\theta + isin\theta)^t + A_2R^t(cos\theta-isin\theta)^t \\
&= A_1R^t(cos\theta t+isin\theta t)+A_2R^t(cos\theta t-isin\theta t)  \qquad de\ Moivre's\ theorem\\
&=\left|\frac{c}{a}\right|^{\frac{t}{2}}(A_1(cos\theta t+isin\theta t)+A_2(cos\theta t-isin\theta t)) \\
&=\left|\frac{c}{a}\right|^{\frac{t}{2}}(B_1cos\theta t+B_2sin\theta t) \qquad \left\{\begin{matrix}
B_1 &= A_1+A_2\\
B_2 &= (A_1-A_2)i
\end{matrix}\right.
\end{align*}$