泰勒级数

泰勒公式（Taylor Series）能把大多数的函数展开成幂级数，即

$f(x) = \displaystyle{ \sum_{n=0}^{\infty}A_n x^n }$

式子当中只有加法与乘法，容易求导，便于理解与计算。这种特性使得泰勒公式在数学推导（如：微分方程以幂级数作为解），数值逼近（如：求e、开方），函数逼近（在计算机某些计算优化时，可以把某些繁琐的式子进行泰勒展开，仅保留加法与乘法运算），复分析等多种应用中有广泛应用。

 

泰勒公式定义

条件：有实函数$f$，$f$在闭区间$[a,b]$是连续的，$f$在开区间$(a,b)$是$n+1$阶可微。

则可以对函数$f$进行泰勒展开：

$\begin{align*}
f(x)
&= \frac{1}{0!}f(x_0) \\
&+\frac{1}{1!}(x-x_0)f'(x_0) \\
&+\frac{1}{2!}(x-x_0)^2f''(x_0) \\
&+ \cdot \cdot \cdot \\
&+\frac{1}{n!}(x-x_0)^nf^{(n)}(x_0) \\
&+ R_n
\end{align*}$

其中$x_0$为区间$(a,b)$中的某一点， $x_0 \in (a,b)$，变量$x$也在区间$(a,b)$内。

泰勒展开得到的是一个多项式，可以写成

$f(x) = \displaystyle{ \sum_{k=0}^{n}\frac{(x-x_0)^k}{k!}f^{(k)}(x) + R_n }$

其中$R_n$为泰勒公式的余项（Remainder）。该余项可以写成以下形式

$R_n = \displaystyle{ \int_{x_0}^x \frac{f^{(n+1)}(t)}{n!}(x-t)^ndt }$

余项$R_n$还可以进一步表示成：存在一点$x_0<\xi<x$使得下面的式子成立

$R_n = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1} $

 

 

泰勒公式推导

泰勒公式推导的起点为微积分基本定理（Fundamental Theorem of Calculus）：

$\displaystyle{ \int_{x_0}^x f'(t)dt } = f(x) – f(x_0)$

因此有：

$\displaystyle{ f(x) = f(x_0) + \int_{x_0}^x f'(t)dt }$

然后用分部积分法(Integration by parts)对积分部分进行分解:

$\begin{align*}
f(x)
&=\color{red}{f(x_0) + \int_{x_0}^x f'(t)dt} \\
&=f(x_0) + \left. tf'(t)\right|_{x_0}^x - \int_{x_0}^x tf''(t)dt \qquad udv = uv - vdu \\
&=f(x_0) + xf'(x) – x_0f'(x_0) - \int_{x_0}^x tf''(t)dt \\
&=f(x_0) + x\left( f'(x_0) + \int_{x_0}^x f''(t)dt \right ) – x_0f'(x_0) - \int_{x_0}^x tf''(t)dt \\
&\qquad Fundamental \ Theorem \ of \ Calculus\\
&=\color{red}{f(x_0) + (x-x_0)f'(x_0) + \int_{x_0}^x (x-t)f''(t)dt} \\
&=f(x_0) + (x-x_0)f'(x_0) + \left.(xt - \frac{1}{2}t^2)f''(t)\right|_{x_0}^x - \int_{x_0}^x(xt - \frac{1}{2}t^2) f'''(t)dt \qquad udv = uv - vdu \\
&=f(x_0) + (x-x_0)f'(x_0) + \frac{x^2}{2}f''(x) + \frac{-2x_0x + {x_0}^2}{2}f''(x_0) - \int_{x_0}^x\frac{2xt-t^2}{2} f'''(t)dt \\
&=f(x_0) + (x-x_0)f'(x_0) + \frac{x^2}{2}\left( f''(x_0) + \int_{x_0}^x f'''(t)dt \right ) + \frac{-2x_0x + {x_0}^2}{2}f''(x_0) \\
&\quad+ \int_{x_0}^x\frac{-2xt+t^2}{2} f'''(t)dt \quad Fundamental \ Theorem \ of \ Calculus\\
&=\color{red}{f(x_0) + (x-x_0)f'(x_0) + \frac{(x-x_0)^2}{2}f''(x_0) + \int_{x_0}^x\frac{(x-t)^2}{2} f'''(t)dt}
\end{align*}$

运用微积分基本定理以及分部积分法继续推导下去可以得到：

$\begin{align*}
f(x)
&= \frac{1}{0!}f(x_0) \\
&+\frac{1}{1!}(x-x_0)f'(x_0) \\
&+\frac{1}{2!}(x-x_0)^2f''(x_0) \\
&+\cdot \cdot \cdot \\
&+\frac{1}{n!}(x-x_0)^nf^{(n)}(x_0) \\
&+\int_{x_0}^x \frac{f^{(n+1)}(t)}{n!}(x-t)^ndt \qquad *
\end{align*}$

由此得到余项

$R_n = \int_{x_0}^x \frac{f^{(n+1)}(t)}{n!}(x-t)^ndt $

 

 

泰勒公式余项推导

泰勒公式的余项能写成多种形式，我们这里只对它的拉格朗日（Lagrange）形式进行推导

拉格朗日余项为：存在一点$x_0<\xi<x$使得下面的式子成立

$R_n = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1} $

 

推导过程如下：

令

$\begin{align*}
F(x)
&=  \frac{1}{0!}f(x_0) \\
&+ \frac{1}{1!}(x-x_0)f'(x_0) \\
&+ \frac{1}{2!}(x-x_0)^2f''(x_0) \\
&+ \cdot\cdot\cdot \\
&+ \frac{1}{n!}(x-x_0)^nf^n(x_0)
\end{align*}$

那么就有

$R_n(x) = f(x) – F(x)$

 

由于$f(x)$与$F(x)$在区间$(a,b)$上都有$n+1$阶导，因此$R_n(x)$在此区间上也有$n+1$阶导。

又因为$R_n(x) = \int_{x_0}^x \frac{f^{(n+1)}(t)}{n!}(x-t)^ndt $，因此有

$R_n(x_0) = R'_n(x_0)=R''_n(x_0) = … = R_n^{(n)}(x_0) = R_n^{(n+1)}(x_0) = 0$

 

对函数$R_n(x)$以及函数$G(x) = (x-x_0)^{n+1}$应用柯西中值定理（Cauchy Mean Value Theorem)，得到:

存在一点$\xi_1 \in (x_0,x)$，使得下面的等式成立

$\frac{R'_n(\xi_1)}{G'(\xi_1)} = \frac{R_n(x) – R_n(x_0)}{G(x) – G(x_0)} $

等号左边展开后为$\frac{R'_n(\xi_1)}{(n+1)(\xi_1-x_0)^n}$，等号右边为$\frac{R_n(x)}{(x-x_0)^{n+1}}$，即

$\frac{R'_n(\xi_1)}{(n+1)(\xi_1 – x_0)^n} = \frac{R_n(x)}{(x-x_0)^{n+1}}$

 

现在注意等号左边，把左边当作对$R'_n(x)$与$(n+1)(x-x_0)^n$在区间$(x_0,\xi_1)$应用柯西中值定理，得到

存在一点$\xi_2 \in (x_0,\xi_1)$，使得下面的等式成立

$\frac{R'_n(\xi_1)}{(n+1)(\xi_1-x_0)^n} = \frac{R'_n(\xi_1)-R'_n(x_0)}{(n+1)(\xi_1-x_0)^n-0}=\frac{R''_n(\xi_2)}{n(n+1)(\xi_2-x_0)^{n-1}}$

 

按照这种方法继续推导下去，经过$n+1$次后得到

$\frac{R_n(x)}{(x-x_0)^{n+1}} = \frac{R^{n+1}_n(\xi)}{(n+1)!}  \qquad (\ \xi\in (x_0,\xi_n)\ ,\ thus \xi \in (x_0,x)\ )$

另外，可以看到$R_n^{(n+1)}(x)=\left( f(x)-F(x) \right)^{(n+1)}=f^{(n+1)}(x)$，代入上面的式子得到

$R_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1} \qquad \xi \in (x_0,x)$

 

 

泰勒级数(Taylor Series)

按照上述泰勒公式，如果$f(x)$在$x_0$处无限可导，那么泰勒公式则变为

$f(x) = \displaystyle{\sum_{n=0}^{\infty}\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + R_{\infty} }$

其中幂级数（Power Series）

$\displaystyle{\sum_{n=0}^{\infty}\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n} $

称为$f(x)$在点$x_0$处的泰勒级数。

 

 

泰勒级数的收敛性分析

泰勒级数在实数域上的收敛性分析

如果函数$f(x)$在包含$x_0$的区间$(a,b)$上无限可导，那么对于所有$x \in (a,b)$，$f(x)$能展开成泰勒级数的条件就是余项在无穷处趋于0，即

$\displaystyle{f(x) = \sum_{n=0}^{\infty}\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \quad \Leftrightarrow \quad \lim_{n\to\infty}R_n(x) = 0 }$

更进一步分析，在泰勒公式时有余项

$R_n(x) = \frac{f^{(n+1)}(\xi_{n+1})}{(n+1)!}(x-x_0)^{n+1} \qquad , \qquad let \ \xi_{n+1} = \xi$

在其前一步，有

$R_{n-1}(x) = \frac{f^{(n)}(\xi_n)}{(n)!}(x-x_0)^{n}$

两者相比，得

$\frac{R_{n}(x)}{R_{n-1}(x)} = \frac{f^{(n+1)} (\xi_{n+1})(x-x_0)}{f^{(n)}(\xi_{n})(n+1) }$

只有$\left| \frac{R_n(x)}{R_{n-1}(x)} \right| < 1$时，才表明余项在变小，即需要

$\left| \frac{f^{(n+1)} (\xi_{n+1})(x-x_0)}{f^{(n)}(\xi_{n})(n+1) } \right| < 1$

$|x-x_0| < \left| \frac{ f^{(n)}(\xi_{n})(n+1) }{ f^{(n+1)}(\xi_{n+1}) } \right|$

否则表明余项在变大。

 

对于泰勒级数来说，如果在$n$趋向于$\infty$时，余项一直在变大，那么表明泰勒级数会越来越远离原来的函数。

 

泰勒级数近似值选取

从上述不等式还可以看出，在求某个点$x=x_1$的近似值时，$x_1$与$x_0$的距离越近，则余项越小，表明误差越小。

也可以参考某乎上的一篇不错的文章。该文章中提到的复数域在下一节有详细推导。

 

泰勒级数在复数域上的收敛性分析

如在实数域收敛分析的时候描述，函数能够展开成泰勒函数的条件是余项在$\infty$处可以收敛。实数域毕竟也只是复数域的一部分，从复数域来分析能帮助我们了解泰勒级数的全貌。

 

复数平面的泰勒级数（Taylor Series in Complex Plane）

复数域的泰勒级数的结构跟实数的泰勒级数一样，只是把函数从实数往复数转变，即

$\displaystyle{ f(z) =\sum_{n=0}^{\infty}\frac{f^{(n)}(z_0)}{n!}(x-x_0)^n}$

其中函数$f$为从复数到复数的映射$f: \mathbb{C} \to \mathbb{C}$，常数为复数$z_0 \in \mathbb{C}$，变量为复数$z \in \mathbb{C}$。该式子可以简化为：

$\displaystyle{ f(z) =  \sum_{n=0}^{\infty}c_n(z-a)^n } \qquad,\qquad z,a,c_n\in\mathbb{C}$

 

收敛圆（Disk of Convergence）

从定义上来说，在复数平面上，如果泰勒级数在某一点$z'$趋于$\infty$，那么就可以说泰勒级数$f(z')$是发散（diverge）的，否则为收敛（converge）。

如果泰勒级数在某有限点处发散的话，那么该泰勒级数的收敛域成一个圆盘（disk）状，称为收敛圆（Disk of Convergence）。该收敛圆的边界与圆心$a$的距离称为收敛半径（Radius of Convergence）$r$。这是泰勒级数的一个特性，下面我们将证明泰勒级数具有这种特性。

 

证明：

假设泰勒级数在有限点$z$处收敛，即有

$\displaystyle{ \sum_{n=0}^{\infty}c_n(z-a)^n } < \infty \qquad , \qquad for \ |z|<\infty$

泰勒级数为无限项求和，因此我们能通过根值判别法（Root test）来分析泰勒级数的收敛性。把$c_n(z-a)^n $看作一个整体，即

$A_n = c_n(z-a)^n $

那么泰勒级数变成$\displaystyle{ \sum_{n=0}^{\infty}A_n  }$，根据Root test，有

$\displaystyle{ C = \limsup_{n\to \infty} \sqrt[n]{ |A_n| } = \limsup_{n\to \infty} \sqrt[n]{ |c_n(z-a)^n| } = \limsup_{n\to \infty} \sqrt[n]{ |c_n| }|z-a| }$

limsup表示的是上极限，$\displaystyle{ \limsup_{n\to\infty} }$表示的是当$n$在无穷远处的上极限。Root test表明了当$C<1$时，泰勒级数收敛；当$C>1$时，泰勒级数发散；当$C=1$时，泰勒级数可能收敛或者发散。

 

我们上面假设泰勒级数在点$z$处收敛，即

$\displaystyle{ C = \limsup_{n\to \infty} \sqrt[n]{ |c_n| }|z-a| < 1 }$

$\displaystyle{ |z - a| < \frac{1}{\limsup_{n\to\infty}\sqrt[n]{c_n} } }$

上面的式子意味着，要使得泰勒级数收敛，$z$与点$a$的距离必须小于

$\displaystyle{r = \frac{1}{\limsup_{n\to\infty}\sqrt[n]{c_n} } }$

对于泰勒级数来说，$a$为选定的无限可导的一点，可以看作圆心，那么收敛域就是一个圆盘，圆盘的半径为$r$。当$r = 1/0$时，意味着半径无穷大，即泰勒级数在整个复数平面上都收敛。

 

收敛半径(Radius of Convergence)求解

在前面证明的时候我们算出了泰勒级数的收敛半径为

$\displaystyle{r = \frac{1}{\limsup_{n\to\infty}\sqrt[n]{c_n} } }$

这看起来不太好计算，下面有另外一种计算方式：

根据比式判别法（Ratio test），只有当下面的式子成立时，泰勒级数收敛

$\displaystyle{ \lim_{n\to\infty}\frac{|A_{n+1}|}{|A_n|} = \lim_{n\to\infty}\frac{|c_{n+1}(z-a)^{n+1}|}{|c_n(z-a)^n|} = \lim_{n\to\infty}\frac{|c_{n+1}(z-a)|}{c_n} < 1 }$

因此有

$r = \displaystyle{ \lim_{n\to\infty}\left| \frac{c_n}{c_{n+1}} \right| = \lim_{n\to\infty}\left| \frac{f^{(n)}(a)(n+1)}{f^{(n+1)}(a)} \right| }$

 

 

泰勒级数与原函数的关系

从复数平面上看，泰勒级数是从选定的某点$a$起，通过$n\to\infty$不断拟合原函数$f$的一种方式，这种拟合的展开是圆心$a$对称的。因此，如果原函数$f$有奇点（singularity：如$\frac{1}{0}$），并且距离$a$最近的奇点为$b$，那么泰勒级数为了拟合原函数，会在$b$点处趋于$\infty$，即在$b$处发散，又由于泰勒级数自身的收敛圆特性，使得泰勒级数无法在收敛圆以外拟合原函数，收敛半径为$|b-a|$。

这也意味着，如果泰勒级数的收敛半径无穷大，那么泰勒级数就能在复数平面上完全拟合原函数，因此泰勒级数等于原函数。

 

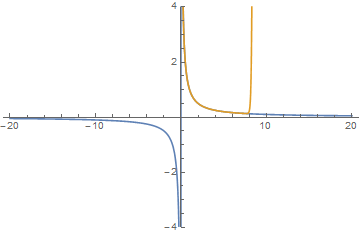
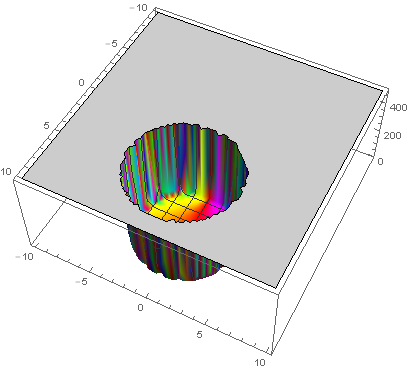
例：

$f(x) = \frac{1}{x}$，选取$a = 4$为无限求导点。当泰勒级数取前50阶时，可以看到：

在实数域，泰勒级数会在$(0,8)$收敛

在复数平面，泰勒级数会以$a = 4+0i$为圆心，收敛半径为$r=4$

 

Mathematica Script

(* Real Domain *)
a = 4;
g[x_] := 1/x;
h[x_, n_] := Normal[Series[g[x], {x, a, n}]];
Manipulate[
 Plot[{g[x], Evaluate[h[x, n]]}, {x, -20, 20}, PlotRange -> 4, 
  PlotLegends -> "Expressions"], {n, 1, 60, 1}]

(* Complex Plane *)
ComplexFnPlot[f_, range_, options___] := 
  Block[{rangerealvar, rangeimagvar, g}, 
   g[r_, i_] := (f /. range[[1]] :> r + I i);
   Plot3D[
    Abs[g[rangerealvar, rangeimagvar]], {rangerealvar, Re[range[[2]]],
      Re[range[[3]]]}, {rangeimagvar, Im[range[[2]]], Im[range[[3]]]},
     options, 
    ColorFunction -> (Hue[Mod[Arg[g[#1, #2]]/(2*Pi) + 1, 1]] &), 
    ColorFunctionScaling -> False]];
ComplexFnPlot[h[z, 50], {z, -10 - 10 I, 10 + 10 I}, 
 PlotRange -> {-4, 500}]