[傅里叶变换及其应用学习笔记] 二十七. 高维傅里叶变换，复习

 

这节课主要讲傅里叶变换的计算，由于高维傅里叶变换有多个变量，多重积分，因此在计算时会有较大的困难。不过某些函数会有较为简捷的计算方式，下面来分析两类这样的函数。

 

可分离函数

有一类函数的高维傅里叶变换能通过计算一系列低维傅里叶变换来得到，这类函数被称为可分离函数。（There's an important class of functions for which you can compute a higher-dimensional transform by computing a series of lower-dimensional transforms. These are separate functions.）

 

例一

二维矩形函数$\Pi(x_1,x_2)$

$\Pi(x_1,x_2)=\begin{cases}
1 & \text{ , } |x_1|<\frac{1}{2}\ \& \ |x_2|<\frac{1}{2} \\
0 & \text{ , } otherwise
\end{cases}$

 

另外，该函数也可以写成两个一维矩形函数的乘积

$\Pi(x_1,x_2) = \Pi(x_1)\Pi(x_2)$

它的傅里叶变换为

$\begin{align*}
\mathcal{F}f(\xi_1,\xi_2)
&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-2\pi i(x_1\xi_1+x_2\xi_2)}\Pi(x_1,x_2)dx_1dx_2\\
&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-2\pi ix_1\xi_1}e^{-2\pi ix_2\xi_2}\Pi(x_1)\Pi(x_2)dx_1dx_2\\
&=\left(\int_{-\infty}^{\infty}e^{-2\pi ix_1\xi_1}\Pi(x_1)dx_1 \right )\left(\int_{-\infty}^{\infty}e^{-2\pi ix_2\xi_2}\Pi(x_2)dx_2 \right )\\
&=\mathcal{F}\Pi(\xi_1)\mathcal{F}\Pi(\xi_2)\\
&=(sinc\xi_1)(sinc\xi_2)
\end{align*}$

 

 

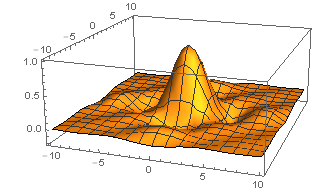
一般来说，如果一个高维函数能写成低维函数的乘积，那么该高维函数的傅里叶变换也能写成这些低维函数的傅里叶变换的乘积。

$f(x_1,x_2,…,x_n) = f_1(x_1)f_2(x_2)…f_n(x_n)$

$\Rightarrow \mathcal{F}f(\xi_1,\xi_2,…,\xi_n) = \mathcal{F}f_1(\xi_1)\mathcal{F}f_2(\xi_2)…\mathcal{F}f_n(\xi_n)$

 

 

例二

二维高斯函数

$g(x_1,x_2) = e^{-\pi(x_1^2+x_2^2)}$

 

它可以分成两个一维高斯函数的乘积

$g(x_1,x_2) = e^{-\pi x_1^2}e^{-\pi x_2^2} = g_1(x_1)g_2(x_2)$

它的傅里叶变换为

$\begin{align*}
\mathcal{F}g(\xi_1,\xi_2)
&=\mathcal{F}g_1(\xi_1)\mathcal{F}g_2(x_2)\\
&=e^{-\pi\xi_1^2}e^{-\pi\xi_2^2}\\
&=e^{-\pi(\xi_1^2+\xi_2^2)}
\end{align*}$

（二维）高斯函数的傅里叶变换是它自身。

 

 

 

径向函数（radial function）

二维高斯函数就是径向函数的一个例子，它是圆对称的。当我们引入极坐标系时，有

$\left.\begin{matrix}
r=\sqrt{x_1^2+x_2^2} \\
\theta=arctan\frac{x_2}{x_1}
\end{matrix} \quad \right| \quad
\left.\begin{matrix}
x_1=rcos\theta \\
x_2=rsin\theta
\end{matrix} \right.$

那么二维高斯函数就可以变为

$g(x_1,x_2) = e^{-\pi(x_1^2+x_2^2)} = e^{-\pi r^2}$

它只依赖于$r$而并非单独的$x_1,x_2$，这就是径向函数的定义。径向函数只依赖于到某原点的距离$r$。

 

径向函数有一个特点：径向函数的傅里叶变换仍是一个径向函数。

证明过程如下：

把笛卡尔坐标系下的傅里叶变换转换成极坐标系形式

笛卡尔坐标系下的傅里叶变换有如下形式

$\displaystyle{ \mathcal{F}f(\xi_1,\xi_2)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-2\pi i(x_1\xi_1+x_2\xi_2)}f(x_1,x_2)dx_1dx_2 }$

变量进行极坐标转换

$\begin{matrix}
x_1=rcos\theta &\qquad \xi_1=\rho cos\varphi \\
x_2=rsin\theta &\qquad \xi_2=\rho sin\varphi
\end{matrix}$

假设$f$是一个径向函数，则$f(x_1,x_2) = f(f)$，$dx_1dx_2$通过极坐标转变成了$rdrd\theta$

复指数内的变量内积变成

$\begin{align*}
x_1\xi_1+x_2\xi_2
&=rcos\theta \rho cos\varphi+rsin\theta \rho sin\varphi\\
&=r\rho(cos\theta cos\varphi+sin\theta sin\varphi)\\
&=r\rho cos(\theta-\varphi)
\end{align*}$

把上述变量代入笛卡尔坐标系下的傅里叶变换式，有

$\begin{align*}
& \quad \int_0^{\infty}\int_0^{2\pi}e^{-2\pi ir\rho cos(\theta-\varphi)}f(r)rdrd\theta\\
&=\int_0^{\infty}\left(\int_0^{2\pi}e^{-2\pi ir\rho cos(\theta-\varphi)}d\theta \right )f(r)rdr\\
&=\int_0^{\infty}\left(\int_0^{2\pi}e^{-2\pi ir\rho cos\theta}d\theta \right )f(r)rdr \\
&\quad (cos\ is\ a\ periodic\ function\ of\ 2\pi\ ,shift\ won't\ effect\ its\ integral)
\end{align*}$

我们把括号内的积分定义成一个函数

$\displaystyle{ J_0(a) = \frac{1}{2\pi}\int_0^{2\pi}e^{-iacos\theta}d\theta }$

$J_0(a)$被称为第一类0阶贝塞尔函数（0'th order bessel function of the first kind），贝塞尔还有其它类，其它阶的函数，它们常出现在径向函数出现的情景中。

结果是，径向函数的二维傅里叶变换通过极坐标系的转换最终变成

$\displaystyle{ \mathcal{F}f(\rho)=2\pi\int_{0}^{\infty}f(r)J_0(2\pi r\rho)rdr }$

它是一个只依赖于$\rho$的函数，而$\varphi$已经在前面对$\theta$的积分处被消除。这个变换被称为0阶汉高变换（0'th order Henkel transformation）。这也证明了径向函数的傅里叶变换仍然是径向函数。

 

 

 

高维傅里叶变换的卷积定理

与一维傅里叶变换的卷积定理一样，它们在高维同样适用

向量形式

$\displaystyle{ (f*g)(\underline{x})=\int_{\mathbb{F}^n}f(\underline{x}-\underline{y})g(\underline{y})d\underline{y} }$

二维分量形式

$\displaystyle{ (f*g)(x_1,x_2)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x_1-y_1,x_2-y_2)g(y_1,y_2)dy_1dy_2 }$

 

以前在分析一维傅里叶变换卷积时，我们不推荐在时域分析卷积，而是把卷积当作是频域的乘积。同样，在这里我们也不推荐在空域分析卷积，因为更多的变量会带来更复杂的思考，幸运的是，卷积在傅里叶变换上的公式在高维仍然适用，即

$\mathcal{F}(f*g)=\mathcal{F}f\mathcal{F}g$

$\mathcal{F}(fg)=\mathcal{F}f * \mathcal{F}g$