[傅里叶变换及其应用学习笔记] 二十二. 快速傅里叶变换
DFT矩阵复习
我们来回顾一下DFT的矩阵运算：对离散信号$\underline{f}$进行DFT，就相当于用DFT矩阵$\underline{\mathcal{F}}$乘以列向量$\underline{f}$
$\begin{pmatrix} 1 &1 &1 &... &1 \\ 1 &\omega^{-1} &\omega^{-2} &... &\omega^{-(N-1)} \\ 1 &\omega^{-2} &\omega^{-4} &... &\omega^{-2(N-1)} \\ \vdots &\vdots &\vdots &... & \vdots\\ 1 &\omega^{-(N-1)} &\omega^{-2(N-1)} &... &\omega^{-(N-1)^2} \end{pmatrix} \begin{pmatrix} \underline{f}[0]\\ \underline{f}[1]\\ \underline{f}[2]\\ \vdots\\ \underline{f}[N-1] \end{pmatrix} = \begin{pmatrix} \underline{\mathcal{F}}\underline{f}[0]\\ \underline{\mathcal{F}}\underline{f}[1]\\ \underline{\mathcal{F}}\underline{f}[2]\\ \vdots\\ \underline{\mathcal{F}}\underline{f}[N-1] \end{pmatrix}$
其中主要的计算量（乘法计算量）为$N \times N$，用$O(N^2)$表示，而FFT可以将计算量降到$NlogN$
FFT的推导的两个方向
1. 矩阵简化
DFT矩阵是$N\times N$维矩阵，但是我们能发现该矩阵中蕴含着一些规律，通过这些规律，对矩阵进行转换，得到一系列多个元素为$0$的矩阵，而矩阵内的元素为$0$意味着减少乘法计算，本课程不会从这个方向着手FFT的推导。
2. 利用复指数的代数性质
1) 引入$\omega[p,q]$
令$\omega[p,q] = e^{2\pi i\frac{q}{p}}$，则$\omega[p,q_1+q_2] = e^{2\pi i\frac{q_1+q_2}{p}} = \omega[p,q_1]\omega[p,q_2]$
那么
$\omega[\frac{N}{2},-1] = e^{-2\pi i\frac{1}{\frac{N}{2}}} = e^{-2\pi i\frac{2}{N}} = \omega[N,-2]$
这表明了$\omega[\frac{N}{2},-1]$是$\omega[N,-1]$的偶次方（平方），因此
$\omega[\frac{N}{2},-n] = \omega[N,-2n]$
等式右边的$2n$代表了偶次方，那么$\omega[N,-1]$的奇次方呢？
$\omega[N,-(2n+1)] = \omega[N,-2n]\omega[N,-1] = \omega[N,-1]\omega[\frac{N}{2},-n]$
现在把$m$也放入到等式中，有
$\omega[N,-2nm] = \omega[\frac{N}{2},-nm]$
$\omega[N,-(2n+1)m] = \omega[N,-m]\omega[\frac{N}{2},-nm]$
另外，
$\omega[N,-\frac{N}{2}] = e^{-2\pi i\frac{\frac{N}{2}}{N}} = e^{-\pi i} = -1$
2) 把DFT公式表达成奇偶项的形式
接下来就是把上述关于$\omega$的奇偶等式代入到DFT公式
首先来回顾一下DFT公式
$\underline{\mathcal{F}}\underline{f}[m] = \displaystyle{ \sum_{n=0}^{N-1}\underline{f}[n]\omega[N,-nm] }$
式子当中共有$N$项多项式相加，我们需要把这$N$项多项式分为奇数与偶数部分，即
$\underline{\mathcal{F}}\underline{f}[m] = (sum\ over\ even\ indices)+(sum\ over\ odd\ indices)$
但是$N$可能不是偶数，这会导致分出来的奇偶项的数目不等，这不符合我们后续的推导过程，因此我们会假设$N$为偶数，即可以按下面的式子进行划分
$\underline{\mathcal{F}}\underline{f}[m] = \displaystyle{ \sum_{n=0}^{\frac{N}{2}-1}\underline{f}[2n]\omega[N,-2nm]+\sum_{n=0}^{\frac{N}{2}-1}\underline{f}[2n+1]\omega[N,-(2n+1)m] }$
我们后面会继续按照这种奇偶项的分解方法一直进行下去，这就要求$N$必须为2的某次方（$N=2^k$）,但是在实际的DFT应用中，可能会出现$N$不为$2^k$的情况，在这种情况下我们就需要在后面补$0$.
$\underline{f} = (\underbrace{ \underline{f}[0],\underline{f}[1],...,\underline{f}[N-1],0,0,...,0 }_{2^k\ entries} )$
有了上述条件，我们回到DFT公式的分解推导，
$\begin{align*}
\underline{\mathcal{F}}\underline{f}
&= \sum_{n=0}^{\frac{N}{2}-1}\underline{f}[2n]\omega[N,-2nm]+\sum_{n=0}^{\frac{N}{2}-1}\underline{f}[2n+1]\omega[N,-(2n+1)m]\\
&= \sum_{n=0}^{\frac{N}{2}-1}\underline{f}[2n]\omega[\frac{N}{2},-nm]+\sum_{n=0}^{\frac{N}{2}-1}\underline{f}[2n+1]\omega[N,-m]\omega[\frac{N}{2},-nm]\\
&= \sum_{n=0}^{\frac{N}{2}-1}\underline{f}[2n]\omega[\frac{N}{2},-nm]+\omega[N,-m]\sum_{n=0}^{\frac{N}{2}-1}\underline{f}[2n+1]\omega[\frac{N}{2},-nm]\\
\end{align*}$
我们来分析一下上述推导结果，上式的奇偶两个大项，基本上可以被当作单独的DFT。其中
- 每个大项的离散数据有$\frac{N}{2}$个，
- 求和从$0到\frac{N}{2}-1$，
- $\omega[\frac{N}{2},-nm] = e^{-2\pi i\frac{nm}{\frac{N}{2}}}$中的复指数分母也由$N$替换成了$\frac{N}{2}$。
但是其中还有一点瑕疵，因为DFT是有多少个输入就会有多少个输出：$\underline{f}$有$N$个输入，则$\underline{\mathcal{F}}\underline{f}$有$N$个输出，也就是说$m = 0,1,…,N-1$；但是$\displaystyle{\sum_{n=0}^{\frac{N}{2}-1}\underline{f}[2n]\omega[\frac{N}{2},-nm]}$只有$\frac{N}{2}$个输入，也只应该有$\frac{N}{2}$个输出，也就是说$m = 0,1,…,\frac{N}{2}-1$，这就与原来的DFT定义相悖了。因此我们可以遵照以下规定
$\underline{\mathcal{F}}_N\underline{f}[m] = \left( \underline{\mathcal{F}}_{\frac{N}{2}}\underline{f}_{even} \right)[m]+\omega[N,-m]\left( \underline{\mathcal{F}}_{\frac{N}{2}}\underline{f}_{odd} \right)[m] \qquad m=0,1,…,\frac{N}{2}$
这样的话只处理了$\underline{\mathcal{F}}\underline{f}$的前半部分，那后半部分该怎么表达呢？
后半部分的输出个数还是为$\frac{N}{2}$，即$m=0,1,…,\frac{N}{2}-1$，然后其他各个部分应该进行相应的变化：
- $\underline{\mathcal{F}}\underline{f}[m]$，变成$\underline{\mathcal{F}}\underline{f}[m+\frac{N}{2}]$
- $\displaystyle{\sum_{n=0}^{\frac{N}{2}-1}}$与$\underline{f}[2n]$、$\underline{f}[2n+1]$，不涉及到$m$，不变
- $\omega[\frac{N}{2},-nm]$，变成$\omega[\frac{N}{2},-n(m+\frac{N}{2})] = \omega[\frac{N}{2},-nm]\omega[\frac{N}{2},-\frac{N}{2}n] = \omega[\frac{N}{2},-nm]$，就是不变
- $\omega[N,-m]$，变成$\omega[N,-(m+\frac{N}{2})] = \omega[N,-m]\omega[N,-\frac{N}{2}] = –\omega[N,-m]$，也就是多了个负号
把上述变化统合起来，有
$\underline{\mathcal{F}}\underline{f}[m+\frac{N}{2}] = \displaystyle{ \sum_{n=0}^{\frac{N}{2}-1}\underline{f}[2n]\omega[\frac{N}{2},-nm]-\omega[N,-m]\sum_{n=}^{\frac{N}{2}-1}\underline{f}[2n+1]\omega[\frac{N}{2},-nm] }$
即
$\underline{\mathcal{F}}_N\underline{f}[m] = \left( \underline{\mathcal{F}}_{\frac{N}{2}}\underline{f}_{even} \right)[m]-\omega[N,-m]\left( \underline{\mathcal{F}}_{\frac{N}{2}}\underline{f}_{odd} \right)[m] \qquad m=0,1,…,\frac{N}{2}$
总结
下面总结一下FFT的计算过程
有$N$元输入的离散信号$\underline{f}$（其中$N=2^k$），我们想推导它的$N$元输出$\underline{\mathcal{F}}\underline{f}$。我们把需要得到的$\underline{\mathcal{F}}\underline{f}$分为前后两半，前半的各项为$\underline{\mathcal{F}}\underline{f}[m]$，后半各项为$\underline{\mathcal{F}}\underline{f}[m+\frac{N}{2}]$，$m=0,1,…,\frac{N}{2}-1$
计算步骤如下
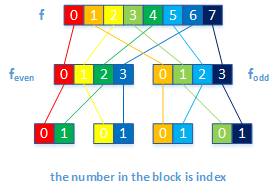
- 把输入$\underline{f}$分成偶数与奇数两个序列$\underline{f}_{even}$，$\underline{f}_{odd}$
- 把$\underline{f}_{even}$，$\underline{f}_{odd}$当作单一的输入，分别计算他们的$\underline{\mathcal{F}}_{\frac{N}{2}}\underline{f}_{even}$，$\underline{\mathcal{F}}_{\frac{N}{2}}\underline{f}_{odd}$
- 通过把$\underline{\mathcal{F}}_{\frac{N}{2}}\underline{f}_{even}$，$\underline{\mathcal{F}}_{\frac{N}{2}}\underline{f}_{odd}$按照下列式子的方式结合起来，可以分别得到$\underline{\mathcal{F}}\underline{f}$的前后半部分
$\underline{\mathcal{F}}_N\underline{f}[m] = \left( \underline{\mathcal{F}}_{\frac{N}{2}}\underline{f}_{even} \right)[m]+\omega[N,-m]\left( \underline{\mathcal{F}}_{\frac{N}{2}}\underline{f}_{odd} \right)[m]$
$\underline{\mathcal{F}}_N\underline{f}[m] = \left( \underline{\mathcal{F}}_{\frac{N}{2}}\underline{f}_{even} \right)[m]-\omega[N,-m]\left( \underline{\mathcal{F}}_{\frac{N}{2}}\underline{f}_{odd} \right)[m]$
$\omega[N,-m] = e^{-2\pi i\frac{m}{N}}\quad,\quad m=0,1,…,\frac{N}{2}-1$
前文推导出的这段计算虽然不能算FFT的全貌，却包含了FFT的主要思想：把一个完整的DFT二分成偶数项$\underline{f}_{even}$以及奇数项$\underline{f}_{odd}$的DFT的组合，然后又再继续对$\underline{f}_{even}$与$\underline{f}_{odd}$继续二分，直到最终剩下两项。
