[傅里叶变换及其应用学习笔记] 九. 继续卷积的讨论

这份是本人的学习笔记，课程为网易公开课上的斯坦福大学公开课：傅里叶变换及其应用。

 

卷积在滤波中的应用

浑浊度（Turbidity）研究是关于测量水的清澈度的研究。大致方法是把光传感器放置到深水区域，然后测量光线的昏暗程度，测量出来的值将随时间变化。

（由于没有真实数据，下面用mathematica比较粗糙地模拟水域的浑浊度数据）

       

能看到信号主要集中在低频，我们需要把毛刺去除，也就是把高频去除，在频域进行低通滤波（Low Pass Filtering）

       

滤波后的波形如下

频域运算：$\pi_{2\nu_c} F(s)$；时域运算为卷积：$2\nu_c sinc(2\nu_c t)*f(t)$。

 

滤波概念

滤波（Filtering）通常等同于卷积，滤波是由滤波器实现的。

滤波器（Filter）是一个输入可变的函数（信号）与一个固定的函数（信号）进行卷积运算的系统。这个固定的信号叫做脉冲响应（impulse response）。

$g \quad = \quad f \qquad * \qquad h$
$\qquad output \qquad input \qquad impulse \ response$

卷积是在时域的表示方法，一般来说，频域的运算会比时域简单许多，因为频域只需执行相乘运算。

$G(s) = F(s)H(s)$

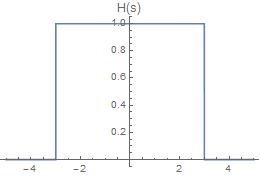
$H(s)$被称为传递函数（transfer function），在设计滤波器时通常是设计合适的传递函数$H(s)$。

 

下面是比较常用的滤波器。

低通滤波器（low pass filter），常用于图像压缩。

高通滤波器（high pass filter），常用于边缘检测（edge detection）

带通滤波器（band pass filter）

 

 

卷积的含义

教授认为只需要从频域理解为函数的相乘即可，而在时域上不需要去具象化卷积。（I think  it is equally idiotic to try to visualize convolution. I think the way to visualize convolution, if there is a way, is to think in terms of multiplying in the frequency domain.）

 

卷积的性质

一般来说$f*g$通常比单独的$f$和$g$更加平滑。

如：矩形函数$\Pi$是不连续的，两个$\Pi$函数的卷积是三角函数$\Lambda$，是连续的。

$\mathcal{F}(\Pi * \Pi) = (\mathcal{F} \Pi)(\mathcal{F} \Pi) = sinc^2 = \mathcal{F} \Lambda$

 

傅里叶导数定理

对原函数进行微分后，它的傅里叶变换等于其原函数的傅里叶变换乘以$2\pi is$

$\mathcal{F}(f')(s) = 2\pi is(\mathcal{F} f)(s)$

证明过程如下：

傅里叶逆变换有：

$f(t) = \displaystyle{\int_{-\infty}^{\infty} F(s)e^{2\pi ist}ds }$

对其求微分，

$\begin{align*}
\frac{\partial f}{\partial t}
&= \int_{-\infty}^{\infty}F(s)(2\pi ise^{2\pi ist})ds \\
&= \int_{-\infty}^{\infty}(2\pi isF(s))e^{2\pi ist}ds \\
\end{align*}$

则有$f'$与$2\pi isF(s)$为傅里叶变换的关系

$f' \ \leftrightarrow \ 2\pi isF(s)$

 

推广开来有

$\mathcal{F}(f^n)(s) = (2\pi is)^n(\mathcal{F} f)(s)$

 

 

无限长柱上的热方程

$U(x,t)$表示时间$t$，位置$x$上的温度。

已知初始温度为$U(x,0) = f(x)$，热方程为$U_t = \frac{1}{2}U_{xx}$。

 

$U(x,t)$的求解过程如下：

对位置变量进行$x$求傅里叶变换，假设变换的结果为$U(s,t)$。

对热方程等号左边进行傅里叶变换，

$\begin{align*}
\mathcal{F}(U_t)
&= \int_{-\infty}^{\infty}e^{-2\pi isx} \frac{\partial}{\partial t}U(x,t)dx  \\
&= \frac{\partial}{\partial t}\int_{-\infty}^{\infty} e^{-2\pi isx}U(x,t)dx \\
&= \frac{\partial}{\partial t}U(s,t)
\end{align*}$

对热方程等号右边进行傅里叶变换，

$\mathcal{F}(\frac{1}{2}U_{xx}) = \frac{1}{2}(2\pi is)^2U(s,t) = –2\pi ^2s^2U(s,t)$

即有

$\frac{\partial}{\partial t}U(s,t) = –2\pi^2s^2U(s,t)$

求偏微分方程，得

$U(s,t) = U(s,0)e^{-2\pi^2s^2t}$

$U(s,0) = \displaystyle{\int_{-\infty}^{\infty}U(x,0)e^{-2\pi isx}dx=\int_{-\infty}^{\infty}f(x)e^{-2\pi isx}dx = F(s) }$

把$U(s,0)$的结果代入$U(s,t)$，得

$U(s,t) = F(s)e^{-2\pi ^2s^2t}$

 

转换为卷积格式

$e^{-2pi ^2s^2t} = \mathcal{F}(\frac{1}{\sqrt{2\pi t}}e^{\frac{x^2}{2t}})$

$\begin{align*}
U(s,t)
&= F(s)e^{-2\pi ^2s^2t}\\
&= (\mathcal{F} f)(\mathcal{F} (\frac{1}{\sqrt{2\pi t}}e^{\frac{x^2}{2t}}))\\
&= \mathcal{F}(f* \frac{1}{\sqrt{2\pi t}}e^{\frac{x^2}{2t}})
\end{align*}$

$U(x,t) = f(x) * \frac{1}{\sqrt{2\pi t}}e^{\frac{x^2}{2t}}$