[傅里叶变换及其应用学习笔记] 五. 傅里叶级数连续性讨论,热方程
这份是本人的学习笔记,课程为网易公开课上的斯坦福大学公开课:傅里叶变换及其应用。
热方程后续
上节课推导出热方程的傅里叶系数:
Ck(t)=Ck(0)e−2π2k2t
那么Ck(0)是什么?
上节课有提到温度有如下关系式:
U(x,t)=∞∑k=−∞Ck(t)e2πikx
当t=0,代表初始时刻圆环上的温度分布
f(x)=U(x,0)=∞∑k=−∞Ck(0)e2πikx
则,Ck(0)为f(x)的傅里叶系数
Ck(0)=ˆf(k)
因此,温度分布公式(热方程)如下:
U(x,t)=∞∑k=−∞ˆf(k)e−2π2k2te2πikx
温度U与时间t的关系为:当t→∞,-2\pi^2k^2t \to –\infty,e^{-2\pi^2k^2t} \to 0,U \to 0。因此,圆环的温度最终会变为0。
热方程进一步推导,引入卷积
我们可以对热方程中的\hat{f}(k)进行进一步分解
\hat{f}(k) = \displaystyle{\int_0^1 e^{-2\pi iky}f(y)dy}
考虑到初始时刻的温度分布f(x)与热方程U(x,t)中的位置变量x可能会取不同的值,我们在此把f(x)写成f(y)。
把\hat{f}(k)代入热方程后,得
\begin{align*} U(x,t) &=\displaystyle{\sum_{k=-\infty}^{\infty}(\int_0^1 e^{-2\pi iky}f(y)dy) e^{-2\pi^2k^2t}e^{2\pi ikx}} \\ &=\displaystyle{\int_0^1(\sum_{k=-\infty}^{\infty}e^{-2\pi iky}e^{2\pi ikx}e^{-2\pi^2k^2t})f(y)dy } \\ &=\displaystyle{\int_0^1(\sum_{k=-\infty}^{\infty}e^{2\pi ik(x-y)}e^{-2\pi^2k^2t})f(y)dy } \end{align*}
令
g(x,t) = \displaystyle{\sum_{k=-\infty}^{\infty}e^{2\pi ikx}e^{-2\pi^2k^2t} }
上面的等式被称为热核方程(heat kernel),则
U(x,t) = \displaystyle{\int_0^1g(x-y,t)f(y)dy }
如上面的等式,热方程被转换成了卷积的表现形式
从傅里叶级数到傅里叶变换
傅里叶级数到傅里叶变换是从周期现象到非周期现象的转变,我们可以将非周期函数看做是周期函数的一种特殊情况:周期趋于无穷。
对于周期为1的函数
C_k = \displaystyle{\hat{f}(k) = \int_0^1e^{-2\pi ikt}f(t)dt }
f(t) = \displaystyle{\sum_{k=-\infty}^{\infty}\hat{f}(k)e^{2\pi ikt} }
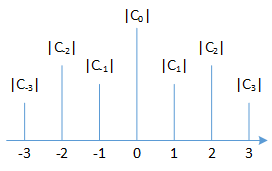
频谱图如下
由于C_k为复数形式,因此我们无法在图上画出,因此只能画出\left | C_k \right | = \left | a + bi \right | = \sqrt{a^2 + b^2}。另外我们在第二节课的时候也学过,C_k是y轴对称的。
对于周期为T的函数
\begin{align*} C_k = \displaystyle{\hat{f}(k) } &= \displaystyle{\frac{1}{T}\int_0^1e^{-\frac{2\pi }{T}ikt}f(t)dt } \\ &= \displaystyle{\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}e^{-2\pi i\frac{k}{T}t}f(t)dt } \end{align*}.
f(t) = \displaystyle{\sum_{k=-\infty}^{\infty}\hat{f}(k)e^{2\pi i\frac{k}{T}t} }
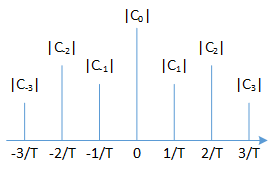
频谱图如下
由于周期为T,因此频率为\frac{1}{T}。当T \to \infty,\frac{1}{T} \to 0,此时频谱会变得连续了。
T \to \infty
但是是否仅仅让T \to \infty就能得到傅里叶变换?答案是否定的,下面来看一个例子
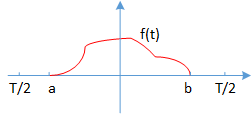
有一个函数f(t)如下图
该函数的傅里叶系数求解过程如下
\begin{align*} C_k = \displaystyle{\hat{f}(k) } &= \displaystyle{\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}e^{-2\pi i\frac{k}{T}t}f(t)dt } \\ &= \displaystyle{\frac{1}{T}\int_a^b e^{-2\pi i\frac{k}{T}t}f(t)dt } \\ &\leqslant \displaystyle{\frac{1}{T}\int_a^b \left | e^{-2\pi i\frac{k}{T}t}\right | \left |f(t) \right |dt } \\ &= \displaystyle{\frac{1}{T}\int_a^b Mod(e^{-2\pi i\frac{k}{T}t}) \left |f(t) \right |dt } \\ &= \displaystyle{\frac{1}{T}\int_a^b Mod(cos(-2\pi \frac{k}{T}t) + isin(-2\pi \frac{k}{T}t)) \left |f(t) \right |dt } \quad spread \ with \ Eular \ Formula \\ &= \displaystyle{\frac{1}{T}\int_a^b \sqrt{cos^2(-2\pi \frac{k}{T}t) + sin^2(-2\pi \frac{k}{T}t)} \left |f(t) \right |dt } \\ &= \displaystyle{\frac{1}{T}\int_a^b 1\left |f(t) \right |dt } \\ &= \displaystyle{\frac{1}{T}\int_a^b \left |f(t) \right |dt } \\ &= \frac{M}{T} \end{align*}.
即对于所有C_k都有C_k \leqslant \frac{M}{T}。
M是该函数绝对值的积分,是有限值,如果T \to \infty,则所有的C_k \to 0。所有傅里叶系数为0则该傅里叶变换毫无意义。



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 自定义通信协议——实现零拷贝文件传输
· Brainfly: 用 C# 类型系统构建 Brainfuck 编译器
· 智能桌面机器人:用.NET IoT库控制舵机并多方法播放表情
· Linux glibc自带哈希表的用例及性能测试
· 深入理解 Mybatis 分库分表执行原理
· DeepSeek 全面指南,95% 的人都不知道的9个技巧(建议收藏)
· 自定义Ollama安装路径
· 本地部署DeepSeek
· 快速入门 DeepSeek-R1 大模型
· DeepSeekV3+Roo Code,智能编码好助手
2012-11-22 IIC原理及简单流程