关于字符串匹配算法研究
第一篇随笔,开始写博客生涯。写程序这么长时间,突然发现也要总结与积累。原来想第一篇博文是关于以前写的代码研究,发现还需要整理。这样,先发表一篇关于字符串
匹配的文章。就这样啦!
字符串匹配主要是关于模式串与主串匹配的问题。关于这个问题,有很多方法。网上也有不少例子,借鉴了不少,以下就介绍下面几种算法。
(1)BF算法(常规算法)
BF算法就是最笨的算法,一个一个进行匹配。这里采用后缀匹配算法。其实与正常的BF算法想法差不多。只不过为了与第四种算法相对应,就用后缀匹配算法代替BF算法。
从网上搞些图(自己实在不想自己画图)

从后面开始进行匹配。当不匹配时,子串整体向右偏移一个单位,再与主串进行比较。从而不断进行循环,直到比较到主串最后一个数。不匹配,则返回-1。否则,返回主
串开始匹配的位置。
Source为主串,SubString为子串。
1 int Search_Reverse(const char *Source,const char *SubString) //后缀缀回溯比较法 (常规BF算法)---为BM算法进行铺垫 2 { 3 int SourceArry = strlen(Source); //主串的长度 4 int SubArry = strlen(SubString); //子串的长度 5 int pSub ,pSour = SubArry; //定义pSub,pSour数值 6 if(SubArry==0) 7 return -1; 8 while(pSour <= SourceArry) //主串是否到了尽头 9 { 10 pSub = SubArry; //初始化 11 while(SubString[--pSub]==Source[--pSour]) //进行匹配比较 12 { 13 if(pSour < 0) return -1; //如果pSour,以子串长度为一组的主串扫描结束 14 15 if(pSub == 0) return pSour; //为0,匹配成功 16 17 } 18 pSour += (SubArry - pSub) +1 ; //进行偏移,pSour值进行恢复与回溯,SubArry - pSub为以前减去的值补回 19 20 } 21 22 return -1; 23 24 }
(2)KMP算法
KMP算法可能一开始理解有点麻烦。不过,有些时候,就要想为什么用KMP匹配算法。比如有子串“abcabd",为什么要用这算法?

当主串中S[5]=“c"与子串T[5]"d"不匹配了,如果采用BF算法进行匹配,则效率偏低。采用KMP算法之后,将子串中的T[0]与主串中的S[3]对齐,再进行比较。因为在子串
中,T[0]~T[1]的字符串与T[3]~T[4]相等,那么刚才第一次匹配时,已经说明S[3]~S[4]与T[3]~T[4]相等,那么也就说明S[3]~S[4]与T[0]~T[1]相等。所以直接将S[5]与
T[2]比较,从这里开始匹配。所以在第一次匹配失败之后,决定从子串中哪个位置再开始进行比较,就是KMP算法中关于Next[]数组的设置。所以KMP算法比BF算法稍微简单一
点,因为我们对于子串做了处理,不用从有时不用从子串T[0]从头开始比较。
基于子串关于Next[]数组的处理,如下:
| 下标i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| p(i) | a | b | c | d | a | a | b | c | a | b |
| next[i] | -1 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 3 | 1 |
也就是对于序列
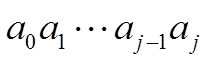
找出这样一个k,使其满足
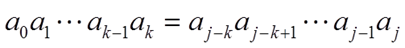
并且要求k尽可能的大!
1 void NextNumber(int Next[],void*S,unsigned int ElemtSize) //对需要查找的字符串进行预处理 2 { 3 4 char *ps = (char*) malloc(ElemtSize); 5 memcpy(ps,S, ElemtSize); 6 int i=strlen(ps); 7 int j = 0; //从头开始计数的j标识 8 int p = 1; //与j进行比较的标识 9 Next[0] = -1; //Next[0] = -1,Next[1] = 0; 10 Next[1] = 0; 11 while(p<i-1) //p<i-1,为循环限制条件 12 { 13 if(ps[p]==ps[j]) 14 { 15 Next[p+1] = j+1 ; //最主要的区别在于,Next[]为一数组,ps又为一数组,且数组之间相差为一 16 ++p; 17 ++j; 18 } 19 else if(j==0) //当j为0时,Next[p+1] = 0;这个有点初始化的味道。 20 { 21 Next[p+1] = 0; 22 ++p; 23 24 } 25 else 26 j = Next[j]; //数组适当进行回退 27 } 28 29 }
Next数组处理好了,接下来就是进行字符串匹配了,即主函数。
1 const int Max = 100; 2 void NextNumber(int Next[],void*S,unsigned int ElemtSize); 3 int KMP(void*T,void*S,unsigned int ElemtSizeT,unsigned int ElemtSizeS) //T为主串,S为子串 4 { 5 char *Ts = (char*) malloc(ElemtSizeT); //将Void做一个转换 6 memcpy(Ts,T,ElemtSizeT); 7 char *Ps = (char*) malloc(ElemtSizeS); 8 memcpy(Ps,S,ElemtSizeS); 9 int Next[Max]; 10 NextNumber(Next,S,ElemtSizeS); 11 int t = 0; 12 int s = 0; 13 int v; //v为偏移距离 14 while(t < ElemtSizeT-1 && (s< ElemtSizeS-1)||s==-1) 15 { 16 if(s == -1|| Ts[t] == Ps[s]) //s为-1时,即比较从头开始,Ts为主串,Ps为子串 17 { 18 ++t;++s; 19 } 20 else 21 s = Next[s]; 22 23 if(s == ElemtSizeS-1) v = t-ElemtSizeS+1; 24 else v = -1; 25 } 26 27 return v; 28 }
上述代码中,字符类型为Void*,不过下面为此做了转换。为什么用此类型,纯属作为实验,尝试用void*类型写一下,大家完全可以用char*.哈哈!
如果还有什么不懂,尽量百度,我发现自己的表达水平果然不怎么样!
(3)Rabin_Karp算法
这个算法是从《算法导论》中借鉴过来的,主要是利用公式。相对来说,前期的工作可能比较辛苦些,主要是做一个Hash表,具体咋样?这里不具体说明。
大概思想就是下面这个图:

其实也就是不断增加找到匹配子串的概率,但也有可能不是,相对来说好一些。当主串中某位置计算出来的值与整个子串计算出来的值相等时,就说明可能在主串这个位置,与
子串相匹配。有这个概率,降低了比较的次数。
算法精华在于在于首先判断出现子串首字母的地方进行标记,然后再进行判断比较
算法利用到了初等算法的理论,两个数对于第三个数等价。
1 int Rabin_Karp_Match( string T,string P,int d,int q) //d为基数/q为除数,最好是一个素数(T为主串,P为子串) 2 { 3 int n = T.length(); 4 int m = P.length(); 5 int h = d^(m-1); 6 int v ; //v为返回值(-1)为失败,其他v值代表匹配的偏移量 7 int p = 0; 8 int t[Max]; 9 t[0] = 0; 10 for(int i=0;i<m;++i) 11 { 12 p=(d*p+P[i])%q; //整个子串计算出来的值 13 t[0]=(d*t[0] +T[i])%q; //t0为T主串首个开始点,方便后面用迭代 14 } 15 for(int j=0;j<n-m;++j) 16 { 17 if(p==t[j]) 18 for(int s=0;s<m;++s) 19 { 20 if(P[s] != T[j]) break; 21 else if(s = m-1) { v = j ; return v ;} 22 else {++s;++j;} 23 } 24 25 if(j<n-m) 26 t[j+1] = (d*(t[j] -T[j+1]*h) +T[j+m])%q; 27 } 28 return -1; 29 30 }
具体参照http://net.pku.edu.cn/~course/cs101/2007/resource/Intro2Algorithm/book6/chap34.htm
(4)BM算法
BM算法可能是相对来说,算法效率最高的一种,一般是KMP算法的3~5倍。
BM算法是从后缀比较法开始的。就是给出的算法(1)代码。然而,普通的后缀比较法一般移动只有1。而BM算法其实是对后缀蛮力匹配算法的改进。为了实现更快移动模式
串,BM算法定义了两个规则,好后缀规则和坏字符规则。用好后缀和坏字符可以大大加快模式串的移动距离,不是简单的 j,而是j =max (shift(好后缀), shift(坏字符))。

具体算法,如下图(网上百度别人博客中的图):
1、坏字符算法(情况分为两种):
- 坏字符没出现在模式串中,这时可以把模式串移动到坏字符的下一个字符,继续比较,如下图:
- 坏字符出现在模式串中,这时可以把模式串第一个出现的坏字符和母串的坏字符对齐,当然,这样可能造成模式串倒退移动,如下图:
为了用代码来描述上述的两种情况,设计一个数组bmBc['k'],表示坏字符‘k’在模式串中出现的位置距离模式串末尾的最大长度,那么当遇到坏字符的时候,模式串可以移动距离为: shift(坏字符) = bmBc[T[i]]-(m-1-i)。如下图:
2、好后缀算法(分为三种情况)
- 模式串中有子串匹配上好后缀,此时移动模式串,让该子串和好后缀对齐即可,如果超过一个子串匹配上好后缀,则选择最靠左边的子串对齐。
- 模式串中没有子串匹配上后后缀,此时需要寻找模式串的一个最长前缀,并让该前缀等于好后缀的后缀,寻找到该前缀后,让该前缀和好后缀对齐即可。
- 模式串中没有子串匹配上后后缀,并且在模式串中找不到最长前缀,让该前缀等于好后缀的后缀。此时,直接移动模式到好后缀的下一个字符。
为了实现好后缀规则,需要定义一个数组suffix[],其中suffix[i] = s 表示以i为边界,与模式串后缀匹配的最大长度,如下图所示,用公式可以描述:满足P[i-s, i] == P[m-s, m]的最大长度s。
好后缀算法比较难理解,理论解释是:
好后缀数组(其中Suffx数组n内数字主要表示好后缀的最右边下标与最左边之间的差值)
i. 如果在P中位置t处已匹配部分P'在P中的某位置t'也出现,且位置t'的前一个字符与位置t的前一个字符不相同,则将P右移使t'对应t方才的所在的位置。
ii. 如果在P中任何位置已匹配部分P'都没有再出现,则找到与P'的后缀P''相同的P的最长前缀x,向右移动P,使x对应方才P''后缀所在的位置。
关于好后缀算法:
1 int *Suff = new int[SubLen]; 2 Suff[SubLen-1] = SubLen; //Suff数组主要记录以数组内标号为子串中的距离 3 4 int *Suff2 = new int[SubLen]; //Suff2数组主要记录下标为以i为首字母的字符后缀离最近的匹配字符串的距离 5 for(int i=0;i<SubLen;i++) 6 Suff2[i] = 0; //初始化为0 7 8 9 for(int i=SubLen-2;i>=0;i--) 10 { 11 int k=i; 12 while(k>=0 && SubString[k] == SubString[SubLen-1-i+k]) //下标SubLen+k-1-i与k相对应(从后面两个数进行比较,从而确定好后缀) 13 { 14 k--; 15 } 16 Suff[i] = i-k; //其中i-k为最右边下标,数组中的下标为i,i代表子串中与最好后缀匹配的位置 17 if(Suff[i] != 0) 18 Suff2[m-Suff[i]] = SubLen-1-i; //确定偏移量 19 } 20 21 int *bmGs = new int[SubLen]; //bmGs数组主要记录当在i处(i处为坏字符),则需要移动的距离 22 for(int i=0;i<SubLen-1;++i) 23 bmGs[i] = SubLen; 24 bmGs[m-1] = 0; 25 26 for(int i=SubLen-2;i >= 0;i--) 27 { 28 if(Suff[m-1-Suff2[i+1]] !=0 && Suff[m-1-Suff2[i+1]]!=11) 29 30 bmGs[i] = Suff2[i+1]; //移动距离S,当与好后缀匹配时,移动距离 31 32 else 33 { 34 35 for(int j=i+2;j<m;j++) 36 if(Suff[m-1-Suff2[j]] == (m-j)) //判断与前缀是否匹配 37 { 38 bmGs[i] = Suff2[j]; //测算出偏移距离 39 break; 40 } 41 42 43 } 44 }
bmGs数组主要记录当在i处(i处为坏字符),则需要移动的距离;Suff2数组,下标表示i处出现坏字符时,在字符串前部最靠近坏字符且与i以后好后缀匹配的字符串的具体位
移量。从而可以测算出具体前部匹配具体坐标。
下面给出具体BM算法:
1 //坏字符算法,主要用来在移动时找到最大位移S,坏字符即移动最大距离 2 void BM_ErrorChar(int SubLen,int CharByte[256],const char *SubString) 3 { 4 //BM_ErrorChar(SubLen,ByteChar); 5 for(int i=0; i<SubLen; ++i) //SubLen-1,不考虑最后一个数 6 CharByte[SubString[i]] = SubLen-i; //如果i最后一个为SubLen-1,则最后一个距离根据计算,需要-1 7 8 } 9 10 11 int BM(const char *Source,const char *SubString) //Source为主串,SubString为子串 12 { 13 int SourceLen = strlen(Source); 14 int SubLen = strlen(SubString); 15 int m=SubLen; 16 //坏字符数组 (其中ByteChar数组的下标为字符,表示此字符出现最后一次离子串尾最近的距离) 17 int ByteChar[256]; //256是因为下标为字符,字符为ASCII码,8位,总共有256种组合 18 for(int i=0;i<256;++i) 19 ByteChar[i] = SubLen; 20 21 22 //int *bmBc = new int[SubLen]; 23 //for(int i=1;i<SubLen;i++) 24 25 26 //好后缀数组(其中Suff数组n内数字主要表示好后缀的最右边下标与最左边之间的差值) 27 // i. 如果在P中位置t处已匹配部分P'在P中的某位置t'也出现,且位置t'的前一个字符与位置t的前一个字符不相同,则将P右移使t'对应t方才的所在的位置。 28 29 // ii. 如果在P中任何位置已匹配部分P'都没有再出现,则找到与P'的后缀P''相同的P的最长前缀x,向右移动P,使x对应方才P''后缀所在的位置。 30 31 32 33 int *Suff = new int[SubLen]; 34 Suff[SubLen-1] = SubLen; //Suff数组主要记录以数组内标号为子串中的距离 35 36 int *Suff2 = new int[SubLen]; //Suff2数组主要记录下标为以i为首字母的字符后缀离最近的匹配字符串的距离 37 for(int i=0;i<SubLen;i++) 38 Suff2[i] = 0; //初始化为0 39 40 41 for(int i=SubLen-2;i>=0;i--) 42 { 43 int k=i; 44 while(k>=0 && SubString[k] == SubString[SubLen-1-i+k]) //下标SubLen+k-1-i与k相对应(从后面两个数进行比较,从而确定好后缀) 45 { 46 k--; 47 } 48 Suff[i] = i-k; //其中i-k为最右边下标,数组中的下标为i,i代表子串中与最好后缀匹配的位置 49 if(Suff[i] != 0) 50 Suff2[m-Suff[i]] = SubLen-1-i; //确定偏移量 51 } 52 53 int *bmGs = new int[SubLen]; //bmGs数组主要记录当在i处(i处为坏字符),则需要移动的距离 54 for(int i=0;i<SubLen-1;++i) 55 bmGs[i] = SubLen; 56 bmGs[m-1] = 0; 57 58 for(int i=SubLen-2;i >= 0;i--) 59 { 60 if(Suff[m-1-Suff2[i+1]] !=0 && Suff[m-1-Suff2[i+1]]!=11) 61 62 bmGs[i] = Suff2[i+1]; //移动距离S,当与好后缀匹配时,移动距离 63 64 else 65 { 66 67 for(int j=i+2;j<m;j++) 68 if(Suff[m-1-Suff2[j]] == (m-j)) //判断与前缀是否匹配 69 { 70 bmGs[i] = Suff2[j]; //测算出偏移距离 71 break; 72 } 73 74 75 } 76 } 77 78 79 //开始BM算法 80 //基于后缀回溯比较法 81 int pSubLen ,pSourLen = SubLen; 82 if(SubLen==0) 83 return -1; 84 while(pSourLen<=SourceLen) //主串是否到了尽头 85 { 86 pSubLen = SubLen; //初始化 87 while(SubString[--pSubLen]==Source[--pSourLen]) //进行匹配比较 88 { 89 90 if(pSourLen < 0) return -1; //如果pSour,以子串长度为一组的主串扫描结束 91 92 if(pSubLen == 0) return pSourLen; //为0,匹配成功 93 94 } 95 BM_ErrorChar(pSubLen,ByteChar,SubString); //计算字符偏移量 96 int CharLen = ByteChar[Source[pSourLen]]; //进行坏字符算法计算CharLen; 97 int SuffLength = bmGs[pSubLen] ; //进行最好后缀法计算出来的偏移长度 98 int MaxLen = MAX(CharLen, SuffLength); //最后后缀算法,分情况讨论 99 pSourLen += (SubLen-pSubLen); 100 pSourLen += MaxLen>1 ? MaxLen:1 ; //进行偏移,pSour值进行恢复与回溯,SubArry - pSub为以前减去的值补回 101 102 } 103 104 return -1; 105 106 }
测试结果:
char *T ="cddcdepcdedefgbcde"; //T为主串
char *S = "cdedefgbcde" ; //S为子串
在T[7]处开始匹配。

引用请注明出处:http://www.cnblogs.com/Su-30MKK/archive/2012/09/17/2688122.html










