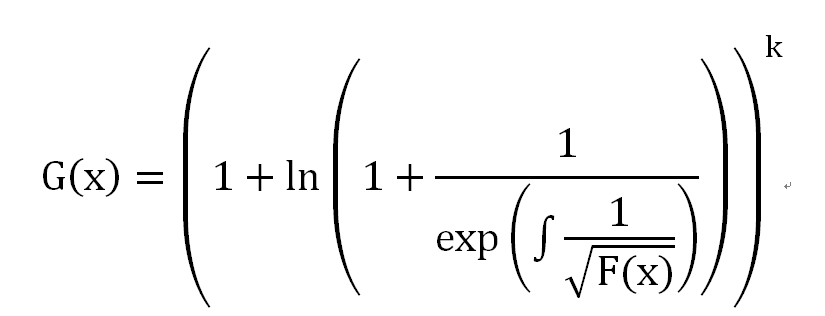多项式计算导论
原创by Sky_miner
定义部分纯属口胡,有不严谨的地方可以在下面评论。
所有代码在最后给出
前置技能
多项式的表示
系数表示法
定义一个多项式\(f(x) = \sum_{i=0}^na_ix^i\)前式之中\(x\)是一个不定元,不表示任何值
则我们可以使用\({a_1,a_2,...,a_{n-1},a_n}\)来表示一个多项式的系数。
其中\(n\)即最高次项的次数则被称作多项式\(f(x)\)的度数或次数,一般记作\(deg_f\)
点值表示法
定义一个多项式\(f(x)\),并用多个点对\((x_i,y_i)\)表示,满足对任意的\(i \text{都有} f(x_i) = y_i\),且这个多项式可以由这些点对唯一确定.
一般点值表示法只用于加速多项式乘法,也就是我们常说的快速傅立叶变换(Fast Fourier Transform, FFT)
复数
复数分为实部和虚部,形式为\(a + bi\)其中\(i^2 = -1\).
复数运算
加法\((a_1+a_2) + (b_1+b_2)i\)
减法\((a_1-a_2) - (b_1-b_2)i\)
乘法\((a_1+b_1i)*(a_2+b_2i) = (a_1*a_2 - b_1*b_2) + (a_1*b_2 + a_2*b_1)i\)
对实数的运算则使实部和虚部同时对那个数进行运算
单位根
\(n\)次单位根为满足\(z^n = 1\)的复数,这样的复数共有\(n\)个且均匀分布在复平面的一个单位圆上。
由数学知识可得,\(n\)次单位根为
且\(e^{θi} = \cos θ + i\sin θ\)
我们记\(\omega_n = e^{\frac{2πi}{n}}\),则\(n\)次单位根为\(\omega_n^0,\omega_n^1,...,\omega_n^{n-1}\)
多项式的求导及积分
求导和积分互为逆运算
求导有:\(g_i = f_{i+1}*(i+1)\)且\(g_n = 0\)
积分有:\(g_i = f_{i-1}/i\)且\(g_0 = 0\)
复杂度均为\(O(n)\)
正片开始:多项式的运算
计算多项式的和即\(A(x) + B(x)\)
即给定多项式\(A(x),B(x)\)
求一个多项式\(C(x)\)满足
系数对位相加,复杂度\(O(n)\);
计算多项式的差即\(A(x) - B(x)\)
即给定多项式\(A(x),B(x)\)
求一个多项式\(C(x)\)满足
系数对位相减,复杂度\(O(n)\);
计算多项式的乘积即\(A(x) * B(x)\)
即给定多项式\(A(x),B(x)\)
求一个多项式\(C(x)\)满足\(C(x) = \sum_{i=0}^{2n}c_ix^i\)
我们可以直接暴力计算,复杂度\(O(n^2)\)
我们之前说过点值表示法主要用于快速计算卷积.卷积通俗地来理解其实就是求所有满足\(i+j\)为一定值的一种计算形势。
所以这里要计算的其实就是一个卷积。
假设说我们多项式是采用的点值表示法,那么我们可以直接把两组点对\((x_i,y_i)\)中所有的点对直接对位相乘,即得到了\((x_i,y_{1_i}*y_{2_i})\)
这样我们就得到了结果多项式的点值表达方式,如果一直采用点值表达的话可以简化乘法运算,但是不利于观察多项式。(毕竟你不能直接看着一堆二元对当多项式用)
所以我们需要一种快速将多项式表示形式转化的一种算法。FFT就是用来处理这个问题的,可以做到在\(O(nlogn)\)内转化完成。所以就可以将乘法的复杂度降低到\(O(nlogn)\)
Cooley-Tukey
该算法的证明及实现网上提到的很多,故不再说明。
(我才不告诉你我不会证明呢)
求多项式的逆元
求多项式\(A(x)\)在\((mod \text{ } x^n)\)意义下的逆元
即对于一个给定的多项式\(f(x)\),求一个多项式\(B(x)\)
满足\(A(x)B(x) \equiv 1 (mod \text{ } x^n)\)
我们仍然采用分治的思想.
假设我们已知一个多项式\(B^{'}(x)\)满足
且我们当前求的多项式\(B(x)\)一定满足
我们将上述两式作差,消掉\(A(x)\)再平方,再乘上\(A(x)\),可以得到
因为\(A(x)B(x) \equiv 1 (mod \text{ } x^n)\)
所以最终化简得到$$B(x) = 2B^{'}(x) - A(x)B{'^2}(x)$$
注:不要忘记在得到的多项式中将所有次数>=mod的次数的项置零.
复杂度\(O(nlogn)\)
多项式的除法和取余
问题即为:给定一个\(n\)次多项式\(A(x)\)和一个\(m\)次多项式\(B(x)\),求出两个多项式\(f(x),g(x)\)满足
且满足\(deg_f \leq n - m,deg_g < m\)
我们发现,如果我们能消去\(g(x)\),就可以人为地规定一个mod,做逆元即可。
所以我们考虑如何消去\(g(x)\)一项.
我们首先定义\(f^R(x) = x^nf(\frac{1}{x})\)
其中\(f^R(x)\)即为\(f(x)\)的系数反转后得到的新的多项式。
(不理解可以自己写几个多项式试一试)
那么我们回到原式的\(A(x) = f(x)B(x) + g(x)\)
我们首先可以不失一般性地设\(deg_f = n-m,deg_g = m-1\)不足则补零.
然后可以做如下变换:
然后我们把这个式子放在\(mod \text{ } x^{n-m+1}\)的剩余系下,可以证明只有最后一项会被模去。
于是我们得到了这么一个式子\(A^R(x) \equiv f^R(x)B^R(x) (mod \text{ } x^{n-m+1})\)
所以我们用刚刚提到的方法求出\(B(x)\)的逆元即可计算出\(f(x)\)
然后\(g(x)\)的计算就不用多说了吧,\(f(x)\)都有了...
复杂度\(O(nlogn)\)
多项式的多点求值
问题即为:给出一个多项式\(A(x)\)和\(n\)个点\(x_0,x_1,...,x_{n-1}\)求\(A(x_0),A(x_1),...,A(s_{n-1})\)
实际上就是多项式向系数表达项点值表达上更一般的转化。由于不具有单位根的特殊性,故不能使用FFT.
但是我们依然可以从Cooley-Tukey的分治策略的角度上想:
我们考虑把求值序列和系数都分半,本别记分开的左右序列为\(X,Y\)
即:
我们设用\(X\)插值得到的序列为\(f(x)\),用\(y\)插值得到的序列为\(g(x)\)
那么我们考虑将其合并为一个新的多项式.
首先我们构造这样的两个多项式
注:因下面的两部分完全相同,故只说明\(F(x)\)的部分
这样,\(F(x)\)的值为零当且仅当\(x \in X\)
那么我们可以有\(A(x) = C(x)F(x) + f(x)\)
这样的话在\(x \in X\)时\(C(x)F(x)\)一定为零,因此可以让\(f(x)\)直接对\(A(x)\)做出贡献
所以此时有\(A(x) \equiv f(x) (mod \text{ } F(x))\)
多项式取余即可.
这样完成了子问题的合并,复杂度\(O(nlog^2n)\)
多项式的快速插值
问题即为:给出\(n+1\)个二元数对\((x_i,y_i)\),要求求出一个\(n\)次多项式使所有的二元数对都在这个多项式上。
实际上就是多项式的点值表达向系数表达上更一般的转化。由于不具有单位根的特殊性,故不能使用FFT.
但是我们依然可以从Cooley-Tukey的分治策略的角度上想:
我们考虑把求值序列分半,本别记分开的左右序列为\(X,Y\)
即:
我们设用\(X\)插值得到的多项式为\(f(x)\),用\(y\)插值得到的序列为\(g(x)\),考虑构造\(A(x)\)
依然设$$F(x) = \prod_{i=0}^{\frac{n}{2}}(x - x_i)$$
则\(A(x) = g(x)F(x) + f(x)\)
那么现在问题就变为了将所有在\(Y\)中的点插值,使得
化简得
所以我们完成了子问题的递归。
复杂度\(O(nlog^3n)\)
多项式求\(ln\)
问题即为:给定多项式\(f(x)\)求一个多项式\(g(x)\)满足\(g(x) = ln\text{ }f(x)\)
我们将两边都求导可得
所以可以在\(O(nlogn)\)内完成
多项式求\(exp\)
问题即为:给定一个多项式\(f(x)\),求一个多项式\(g(x)\)满足\(g(x) = e^f(x)\)
我们采用分治策略.
(这个公式我不会证)
设\(g_0(x)\)为子问题\((1~\frac{n}{2})\)中得到的结果
则我们有\(g(x) = g_0(x)*(1 - lng_0(x) + f(x))\)
迭代可以在\(O(nlog^2n)\)内完成
多项式开根号
问题即为:给定一个多项式\(f(x)\)求出一个多项式\(g(x)\)满足g^2(x) = f(x)
我们设\(g_0^2(x) \equiv f(x)(mod \text{ } x^{\frac{n}{2}})\)
呢么我们有
那么我们就发现:
利用分治算法,我们可以在\(O(nlogn)\)内完成
但是常数巨大,我们可以把常数也算成一个\(log\),也就是\(O(nlog^2n)\)
多项式快速幂
问题即为:给定一个多项式\(f(x)\)和一个整数\(k\)求一个多项式\(g(x)\)满足\(g(x) \equiv f^k(x) (mod \text{ } x^n)\)
正常选手: 我们可以多次FFT每次除去所有次数>=n的项。
脑洞选手: 我们可以输出\(exp(k\text{ }ln\text{ }f(x))\)
Code:
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
template<typename T>inline void read(T &x){
x=0;char ch;bool flag = false;
while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true;
while(x=10*x+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
const int pri_rt = 3;
const int maxn=600010;
const int mod=998244353;
const int inv_2 = 499122177;
int n,k,N,C,len;
int rev[maxn],w[maxn];
int f[maxn];
int Inv[maxn],Ln[maxn],Exp[maxn],Sqrt[maxn];
inline int qpow(int x,int p){
int ret = 1;
for(;p;x=1LL*x*x%mod,p>>=1) if(p&1) ret=1LL*ret*x%mod;
return ret;
}
inline int check(int &x){
if(x < 0) x += mod;
if(x >= mod) x -= mod;
}
void FNT(int n,int *x,int flag){
for(int i=0,t=0;i<n;++i){
if(i > t) swap(x[i],x[t]);
for(int j=n>>1;(t^=j) < j;j>>=1);
}
for(int m=2;m<=n;m<<=1){
int k = m>>1;
int wn = qpow(pri_rt,flag == 1 ? (mod - 1)/m : (mod-1) - (mod-1)/m);
w[0] = 1;
for(int i=1;i<k;++i) w[i] = 1LL*w[i-1]*wn % mod;
for(int i=0;i<n;i+=m){
for(int j=0;j<k;++j){
int u = 1LL*x[i+j+k]*w[j] % mod;
x[i+j+k] = x[i+j] - u;check(x[i+j+k]);
x[i+j] = x[i+j] + u;check(x[i+j]);
}
}
}
if(flag == -1){
int inv = qpow(n,mod-2);
for(int i=0;i<n;++i) x[i] = 1LL*x[i]*inv%mod;
}
}
inline void get_dao(int n,int *f){
for(int i=0;i<n;++i) f[i] = 1LL*f[i+1]*(i+1) % mod;
f[n] = 0;
}
inline void get_fen(int n,int *f){
for(int i=n-1;i>=0;--i) f[i] = 1LL*f[i-1]*qpow(i,mod-2) % mod;
f[0] = 0;
}
void get_inv(int n,int *f){
static int g[maxn];
if(n == 1){
Inv[0] = qpow(f[0],mod-2);
return;
}
get_inv((n+1)>>1,f);
int len = n<<1;
for(int i=0;i<n;++i) g[i] = f[i];
fill(g+n,g+len,0);
FNT(len,g,1);FNT(len,Inv,1);
for(int i=0;i<len;++i){
Inv[i] = 1LL*Inv[i]*(2LL - 1LL*g[i]*Inv[i]%mod + mod) % mod;
}FNT(len,Inv,-1);fill(Inv+n,Inv+len,0);
}
void get_ln(int n,int *f){
int len = n<<1;
fill(Inv,Inv+(len<<1),0);
get_inv(n,f);get_dao(n,f);
FNT(len,f,1);FNT(len,Inv,1);
for(int i=0;i<len;++i) Ln[i] = 1LL*f[i]*Inv[i] % mod;
FNT(len,Ln,-1);fill(Ln+n,Ln+len,0);
get_fen(n,Ln);
}
void get_exp(int n,int *f){
static int g[maxn];
if(n == 1){
Exp[0] = 1;
return;
}
get_exp(n>>1,f);
int len = n<<1;
for(int i=0;i<n;++i) g[i] = Exp[i];
fill(g+n,g+len,0);
get_ln(n,g);
for(int i=0;i<n;++i) Ln[i] = ((i == 0) - Ln[i] + f[i] + mod) % mod;
FNT(len,Ln,1);FNT(len,Exp,1);
for(int i=0;i<len;++i) Exp[i] = 1LL*Exp[i]*Ln[i] % mod;
FNT(len,Exp,-1);fill(Exp+n,Exp+len,0);
}
void get_sqrt(int n,int *f){
static int g[maxn];
if(n == 1){
Sqrt[0] = sqrt(f[0]);
return;
}
get_sqrt(n>>1,f);
int len = n<<1;
fill(Inv,Inv+(len<<1),0);get_inv(n,Sqrt);
for(int i=0;i<n;++i) g[i] = f[i];
fill(g+n,g+len,0);
FNT(len,g,1);FNT(len,Inv,1);
for(int i=0;i<len;++i) g[i] = 1LL*g[i]*Inv[i] % mod;
FNT(len,g,-1);
for(int i=0;i<n;++i) Sqrt[i] = 1LL*(Sqrt[i] + g[i])*inv_2%mod;
}
void get_pow(int len,int *f,int p){
get_ln(len,f);
for(int i=0;i<len;++i) f[i] = 1LL*p*Ln[i]%mod;
fill(Exp,Exp+(len<<1),0);
get_exp(len,f);
}
int main(){
int n,k;read(n);read(k);
for(int i=0;i<n;++i) read(f[i]);
for(len=1;len<=n;len<<=1);
get_sqrt(len,f);
fill(Inv,Inv+(len<<1),0);get_inv(len,Sqrt);
for(int i=0;i<len;++i) f[i] = Inv[i];
get_fen(len,f);fill(f+n,f+len,0);
get_exp(len,f);
for(int i=0;i<len;++i) f[i] = Exp[i];
fill(Inv,Inv+(len<<1),0);get_inv(len,f);
for(int i=0;i<len;++i) f[i] = Inv[i];
++f[0];
get_ln(len,f);
for(int i=0;i<len;++i) f[i] = Ln[i];
++f[0];
fill(f+len+1,f+(len<<1),0);
get_pow(len,f,k);
for(int i=1;i<n;++i) printf("%d ",1LL*Exp[i]*i % mod);
puts("0");
getchar();getchar();
return 0;
}
该代码用于计算这样的一个式子