方差

题目背景

滚粗了的HansBug在收拾旧数学书，然而他发现了什么奇妙的东西。

题目描述

蒟蒻HansBug在一本数学书里面发现了一个神奇的数列，包含N个实数。他想算算这个数列的平均数和方差。

输入输出格式

输入格式：

第一行包含两个正整数N、M，分别表示数列中实数的个数和操作的个数。

第二行包含N个实数，其中第i个实数表示数列的第i项。

接下来M行，每行为一条操作，格式为以下两种之一：

操作1：1 x y k ，表示将第x到第y项每项加上k，k为一实数。

操作2：2 x y ，表示求出第x到第y项这一子数列的平均数。

操作3：3 x y ，表示求出第x到第y项这一子数列的方差。

输出格式：

输出包含若干行，每行为一个实数，即依次为每一次操作2或操作3所得的结果（所有结果四舍五入保留4位小数）。

输入输出样例

输入样例#1：

5 5
1 5 4 2 3
2 1 4
3 1 5
1 1 1 1
1 2 2 -1
3 1 5

输出样例#1：

3.0000
2.0000
0.8000

分析

线段树，是个好东西呀，这道题很容易想到线段树维护，嘤嘤嘤，很好想到啊！！

我去，发现，插入不了数学公式，插入不了任何有用的东西，烦死人，只好手打了呢！！

额，好吧，我来插入图片啦！！

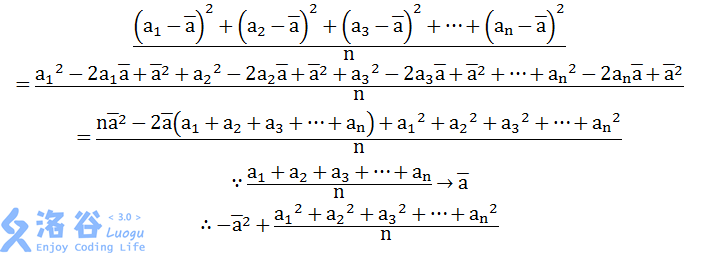
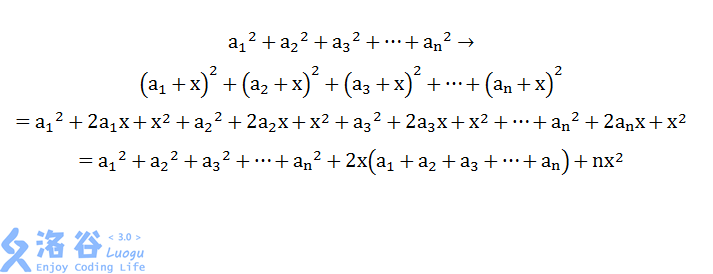
图片取自luogu，感谢啦。
由此可以看出只要用线段树维护区间和，和区间平方和即可，呃呃呃呃，当然还要个下推标记啦，烦死人。。。

#include <cstdio>
#include <cmath>
#include <deque>
#include <stack>
#include <queue>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
#define ll long long
#define ull unsigned long long

const int Maxn=20041108;
const int inf=20040207;
const int I_LOVE_XYY=5201314

int n,m,x,y,z;double k;
struct node { int l,r; double w,v,s; }tree[Maxn*4];
void build_tree(int index,int l,int r) {
    tree[index].l=l;
    tree[index].r=r;
    tree[index].w=tree[index].s=tree[index].v=0;
    if(l==r) {
        cin>>k;
        tree[index].w=k;
        tree[index].s=k*k;
        tree[index].v=k;
        return;
    }
    int mid=(l+r)/2;
    build_tree(index*2,l,mid);
    build_tree(index*2+1,mid+1,r);
    tree[index].w=tree[index*2].w+tree[index*2+1].w;
    tree[index].s=tree[index*2].s+tree[index*2+1].s;
}
void pushdown(int index) {
    if(tree[index].v) {
        tree[index*2].s+=2*tree[index].v*tree[index*2].w+(tree[index*2].r-tree[index*2].l+1)*tree[index].v*tree[index].v;
        tree[index*2+1].s+=2*tree[index].v*tree[index*2+1].w+(tree[index*2+1].r-tree[index*2+1].l+1)*tree[index].v*tree[index].v;
        tree[index*2].w+=tree[index].v*(tree[index*2].r-tree[index*2].l+1);
        tree[index*2+1].w+=tree[index].v*(tree[index*2+1].r-tree[index*2+1].l+1);
        tree[index*2].v+=tree[index].v;
        tree[index*2+1].v+=tree[index].v;
        tree[index].v=0;
    }
}
void change_tree(int index,int l,int r,double k) {
    if(tree[index].l>=l&&tree[index].r<=r) {
        tree[index].v+=k;
        tree[index].s+=2*k*tree[index].w+k*k*(tree[index].r-tree[index].l+1);
        tree[index].w+=k*(tree[index].r-tree[index].l+1);
        return;
    }
    int mid=(tree[index].l+tree[index].r)/2;
    pushdown(index);
    if(l<=mid) change_tree(index*2,l,r,k);
    if(r>mid) change_tree(index*2+1,l,r,k);
    tree[index].w=tree[index*2].w+tree[index*2+1].w;
    tree[index].s=tree[index*2].s+tree[index*2+1].s;
}
double query_x(int index,int l,int r) {
    if(tree[index].l>=l&&tree[index].r<=r) return tree[index].w;
    double ans=0;
    int mid=(tree[index].l+tree[index].r)/2;
    pushdown(index);
    if(l<=mid) ans+=query_x(index*2,l,r);
    if(r>mid) ans+=query_x(index*2+1,l,r);
    return ans;
}    
double query_y(int index,int l,int r) {
    if(tree[index].l>=l&&tree[index].r<=r) return tree[index].s;
    double ans=0;
    int mid=(tree[index].l+tree[index].r)/2;
    pushdown(index);
    if(l<=mid) ans+=query_y(index*2,l,r);
    if(r>mid) ans+=query_y(index*2+1,l,r);
    return ans;
}    
int main() {
    cin>>n>>m;
    build_tree(1,1,n);
    while(m--) {
        cin>>z>>x>>y;
        if(z==1) {
            cin>>k;
            change_tree(1,x,y,k);
        }
        else if(z==2) printf("%.4lf\n",query_x(1,x,y)/(y-x+1));
        else {
            double dx=query_x(1,x,y)/(y-x+1);
            double dy=query_y(1,x,y)/(y-x+1);
            printf("%.4lf\n",dy-dx*dx); 
        }    
    }
    return 0;
}

下推标记和查询输出，可以看出充分利用了上述两个公式来操作，是个不错的题目，qwq。。。

此题需要数学期末考试在145以上的同学才可以尝哟！！

因为我都不会啊啊啊啊，那是不可能的，但我考不到145也会做，哈哈哈哈哈！！！