模拟退火法
一. 爬山算法 ( Hill Climbing )
介绍模拟退火前,先介绍爬山算法。爬山算法是一种简单的贪心搜索算法,该算法每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。
爬山算法实现很简单,其主要缺点是会陷入局部最优解,而不一定能搜索到全局最优解,如图。
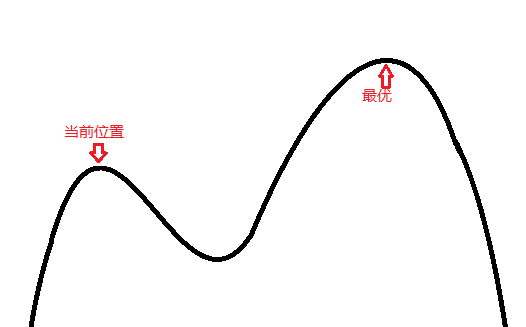
如果坚决不接受一个更差的解,那么就会卡在上面的“当前位置”上了。倘若接受多几次更差的解,让他移动到山谷那里,则可以突破局部最优解,得到全局最优解。
既然这个随机这么重要,那么我们就将它写为一个函数:
bool accept(double delta, double temper){
if(delta <= 0) return true;
return rand() <= exp((-delta) / temper) * RAND_MAX;
}
其中delta是新答案的变化量,temper是当前的“温度”。温度是模拟退火算法的一个重要概念,它随时间的推移缓慢减小。我们来分析一下这个代码:
if(delta <= 0) return true;
由于答案越小越优,因此当温度的变化量小于零(新答案减小)时,新解比旧解优,因此返回“接受”
return rand() <= exp((-delta) / temper) * RAND_MAX;
RAND_MAX是rand()的最大值。为了保证跨平台、跨编译器甚至跨版本时的正常运作,我们不对其作出任何假定。
我们把它移项:return (double)rand() / RAND_MAX <= exp((-delta) / temper)。在右边,temper是正数,delta是正数(delta是负数的已经return出去了),因此exp()中间的参数是负数。我们知道,指数函数在参数是负数时返回(0, 1)——这就是接受的概率。我们在左边随机一个实数,如果它比概率小,就接受,否则就不接受。
然后将RAND_MAX移到右边,以省下昂贵的除法成本和避免浮点数的各种陷阱。
总结起来就是:
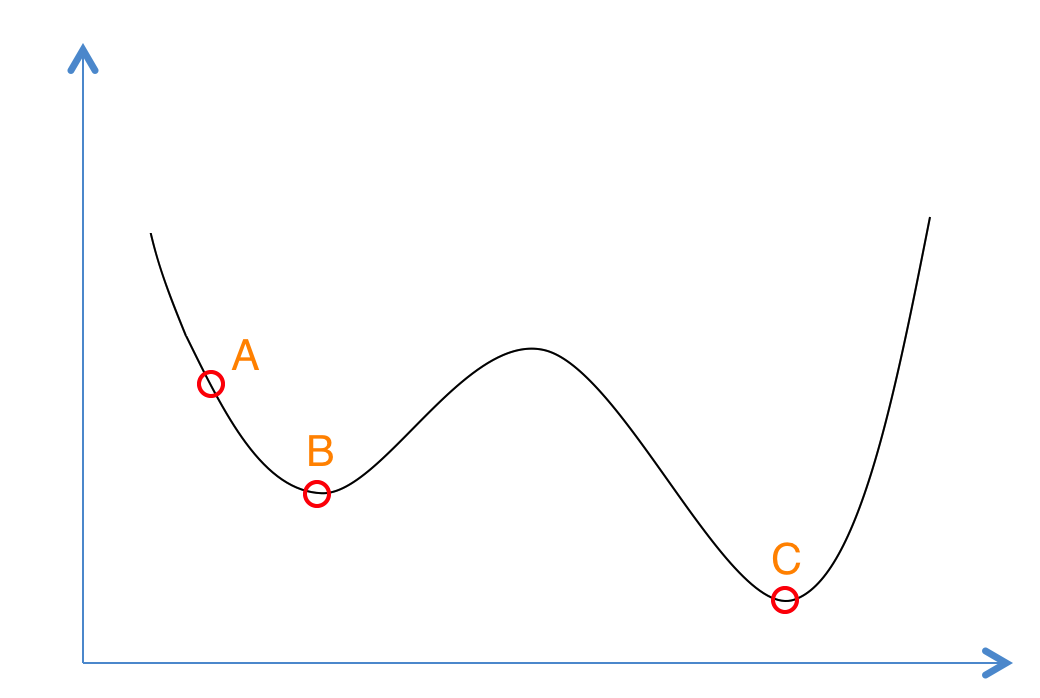
- 若f( Y(i+1) ) <= f( Y(i) ) (即移动后得到更优解),则总是接受该移动;
- 若f( Y(i+1) ) > f( Y(i) ) (即移动后的解比当前解要差),则以一定的概率接受移动,而且这个概率随着时间推移逐渐降低(逐渐降低才能趋向稳定)相当于上图中,从B移向BC之间的小波峰时,每次右移(即接受一个更糟糕值)的概率在逐渐降低。如果这个坡特别长,那么很有可能最终我们并不会翻过这个坡。如果它不太长,这很有可能会翻过它,这取决于衰减 t 值的设定。
计算过程:
double solve(){ const double max_temper = 10000; double temp = max_temper; double dec = 0.999; Path p; while(temp > 0.1){ Path p2(p); if(accept(p2.dist() - p.dist(), temp)) p = p2; temp *= dec; } return p.dist(); }
好了,懂了这些来道题
https://vijos.org/p/1153 正规解法:vijos1153 猫狗大战
通过对拍可发现有部分点是过不了的,是应为程序从正确的点通过错误的接受到了一个错误的点并因为概率的减小卡住了。
能怎么能提高通过率,记下到达过的最优点即可。

1 #include<iostream> 2 #include<algorithm> 3 #include<cstdio> 4 #include<cstring> 5 #include<cmath> 6 #include<cstdlib> 7 #include<vector> 8 using namespace std; 9 typedef long long ll; 10 typedef long double ld; 11 typedef pair<int,int> pr; 12 const double pi=acos(-1); 13 #define rep(i,a,n) for(int i=a;i<=n;i++) 14 #define per(i,n,a) for(int i=n;i>=a;i--) 15 #define Rep(i,u) for(int i=head[u];i;i=Next[i]) 16 #define clr(a) memset(a,0,sizeof(a)) 17 #define pb push_back 18 #define mp make_pair 19 #define fi first 20 #define sc second 21 #define pq priority_queue 22 #define pqb priority_queue <int, vector<int>, less<int> > 23 #define pqs priority_queue <int, vector<int>, greater<int> > 24 #define vec vector 25 ld eps=1e-9; 26 ll pp=1000000007; 27 ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;} 28 ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;} 29 void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); } 30 //void add(int x,int y,int z){ v[++e]=y; next[e]=head[x]; head[x]=e; cost[e]=z; } 31 int dx[5]={0,-1,1,0,0},dy[5]={0,0,0,-1,1}; 32 ll read(){ ll ans=0; char last=' ',ch=getchar(); 33 while(ch<'0' || ch>'9')last=ch,ch=getchar(); 34 while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar(); 35 if(last=='-')ans=-ans; return ans; 36 } 37 #define N 205 38 bool accept(double delta, double temper){ 39 if(delta <= 0) return true; 40 int t=rand() <= exp((-delta) / temper) * RAND_MAX; 41 //cout<<t<<endl; 42 return t; 43 } 44 int a[N],c[N]; 45 int main() 46 { 47 srand(0); 48 int n=read(),d=0,ans_1=0,ans_2=0,ans1=0,ans2=0; 49 for (int i=1;i<=n;i++) a[i]=read(); 50 if (n==1) { 51 cout<<"0 "<<a[1]<<endl; 52 return 0; 53 } 54 for (int i=1;i<=(n/2);i++) ans_1+=a[i],c[i]=1; 55 for (int i=(n/2)+1;i<=n;i++) ans_2+=a[i],c[i]=0; 56 ans1=ans_1; ans2=ans_2; 57 d=abs(ans_1-ans_2); 58 double T=1000000; 59 while (T>0.00001){ 60 int x=rand()%n+1,y=rand()%n+1,ans_1_=ans_1,ans_2_=ans_2; 61 while (!c[x]) x=rand()%n+1; while (c[y]) y=rand()%n+1; 62 ans_1_+=a[y]-a[x]; ans_2_+=a[x]-a[y]; 63 int d_=abs(ans_1_-ans_2_); 64 if (accept((double)(d_-d),T)) c[x]=0,c[y]=1,d=d_,ans_1=ans_1_,ans_2=ans_2_; 65 if (abs(ans1-ans2)>abs(ans_1-ans_2)) ans1=ans_1,ans2=ans_2; 66 T*=0.9999; 67 } 68 if (ans1<ans2) cout<<ans1<<" "<<ans2; 69 else cout<<ans2<<" "<<ans1; 70 return 0; 71 }
参考:
http://www.cnblogs.com/CsOH/p/6049117.html
http://www.cnblogs.com/heaad/archive/2010/12/20/1911614.html



