Manthan, Codefest 16
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) {
Scanner cin = new Scanner (new BufferedInputStream (System.in));
int a = cin.nextInt ();
int b = cin.nextInt ();
int c = cin.nextInt ();
for (int i=0; a*i<=c; ++i) {
int d = c - a * i;
if (d % b == 0) {
System.out.println ("Yes");
return ;
}
}
System.out.println ("No");
}
}
题意:问n!的后缀0的个数为m个的n的范围.
分析:出现0的一定是2*5产生的,而2的数字有很多,所以找到最小的数字之前5的总个数为m的.二分来找.
#include <bits/stdc++.h>
int number(int x) {
int ret = 0;
while (x) {
x /= 5;
ret += x;
}
return ret;
}
int main() {
int m; scanf ("%d", &m);
int left = 1, right = (int) 1e9;
while (left < right) {
int mid = left + right >> 1;
if (number (mid) < m) left = mid + 1;
else right = mid;
}
std::vector<int> ans;
for (;;) {
if (number (left) == m) ans.push_back (left);
else break;
left++;
}
int sz = ans.size ();
printf ("%d\n", sz);
for (int i=0; i<sz; ++i) {
if (i > 0) putchar (' ');
printf ("%d", ans[i]);
}
puts ("");
return 0;
}
Trie + DP C - Spy Syndrome 2
题意:有一句话被变成全小写并且删掉空格并且翻转单词,然后给出可能的单词.问原来可能的这句话.
分析:首先把单词插入到字典树上,这里为了节约内存把所有单词并在一起.结点保存了该单词在单词串的位置以便输出.然后文本串倒过来在字典树上DP搜索,最后正的输出,那么可以找到可行的一句话.
#include <bits/stdc++.h>
const int N = 1e4 + 5;
const int M = 1e6 + 1e5;
const int NODE = M;
char text[N], words[M];
int ch[NODE][26], val[NODE], pos[NODE];
int n, m, sz;
int nex[N], wl[N];
int idx(char c) {
return tolower (c) - 'a';
}
void trie_init() {
memset (ch[0], 0, sizeof (ch[0]));
sz = 1;
}
void trie_insert(char *str, int end, int id, int p) {
int u = 0;
for (int c, i=0; i<end; ++i) {
c = idx (str[i]);
if (!ch[u][c]) {
memset (ch[sz], 0, sizeof (ch[sz]));
val[sz] = 0; pos[sz] = 0;
ch[u][c] = sz++;
}
u = ch[u][c];
}
val[u] = id; pos[id] = p;
}
void trie_query() {
memset (nex, -1, sizeof (nex));
memset (wl, 0, sizeof (wl));
nex[n] = 0;
for (int i=n; i>0; --i) {
if (nex[i] == -1) continue;
int u = 0;
for (int c, j=i-1; j>=0; --j) {
c = idx (text[j]);
if (!ch[u][c]) break;
u = ch[u][c];
if (val[u] > 0) {
wl[j] = pos[val[u]];
nex[j] = i;
}
}
}
}
int main() {
scanf ("%d", &n);
scanf ("%s", text);
scanf ("%d", &m);
trie_init ();
for (int L=0, i=1; i<=m; ++i) {
scanf ("%s", words + L);
int len = strlen (words + L);
trie_insert (words + L, len, i, L);
L += len + 1;
}
trie_query ();
int now = 0;
while (now < n) {
if (now > 0) putchar (' ');
printf ("%s", words + wl[now]);
now = nex[now];
}
puts ("");
return 0;
}
DFS + 二分 D - Fibonacci-ish
题意:在n个数找出一组数字满足fn = fn-1 + fn-2, 问最大长度.
分析:n的范围小,可以考虑n^2枚举两个起点,因为要考虑到个数的问题,这里我选择一种方便的写法:首先不考虑个数,只预处理两个数能否到下一个数字.然后考虑个数,类似DFS的vis功能,深搜时-1,回溯时+1
#include <bits/stdc++.h>
const int N = 1e3 + 5;
const int MOD = 1e9 + 7;
int a[N], A[N];
int nex[N][N];
int cnt[N];
int ans;
void DFS(int i, int j, int step) {
if (step > ans) ans = step;
int k = nex[i][j];
if (k == -1) return ;
else if (cnt[k] > 0) {
--cnt[k];
DFS (j, k, step + 1);
++cnt[k];
}
}
int main() {
int n; scanf ("%d", &n);
for (int i=0; i<n; ++i) {
scanf ("%d", &a[i]); A[i] = a[i];
}
std::sort (A, A+n);
int m = std::unique (A, A+n) - A;
for (int i=0; i<n; ++i) {
a[i] = std::lower_bound (A, A+m, a[i]) - A;
cnt[a[i]]++;
}
for (int i=0; i<m; ++i) {
for (int j=0; j<m; ++j) {
int k = std::lower_bound (A, A+m, A[i] + A[j]) - A;
if (k >= m || A[i] + A[j] != A[k]) nex[i][j] = -1;
else nex[i][j] = k;
}
}
ans = 2;
for (int i=0; i<m; ++i) {
--cnt[i];
for (int j=0; j<m; ++j) {
if (cnt[j] <= 0) continue;
--cnt[j];
DFS (i, j, 2);
++cnt[j];
}
++cnt[i];
}
printf ("%d\n", ans);
return 0;
}
二分查找 + RMQ + 组合数学 E - Startup Funding
题意:对于每一个li = i,找到一个ri,使得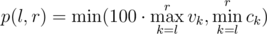
最大.从n个结果中选择k个,最小值的期望.
分析:第一个问题,考虑前缀max (vk)是递增的,考虑前缀min(ck)是递减的,两者取min那么是单峰函数,二分查找.第二个问题,首先对结果排序,假设最小值为ans[i],那么选中它当最小值的概率是C(n-i, k-1) / C (n, k).p * ans[i]求和就是期望.发现公式可以递推.
#include <bits/stdc++.h>
const int N = 1e6 + 5;
int mx[N][21], mn[N][21];
int best[N];
int n, k;
void build_max() {
for (int j=1; (1<<j)<=n; ++j) {
for (int i=1; i+(1<<j)-1<=n; ++i) {
mx[i][j] = std::max (mx[i][j-1], mx[i+(1<<(j-1))][j-1]);
}
}
}
int query_max(int l, int r) {
int k = 0; while (1<<(k+1) <= r-l+1) ++k;
return std::max (mx[l][k], mx[r-(1<<k)+1][k]);
}
void build_min() {
for (int j=1; (1<<j)<=n; ++j) {
for (int i=1; i+(1<<j)-1<=n; ++i) {
mn[i][j] = std::min (mn[i][j-1], mn[i+(1<<(j-1))][j-1]);
}
}
}
int query_min(int l, int r) {
int k = 0; while (1<<(k+1) <= r-l+1) ++k;
return std::min (mn[l][k], mn[r-(1<<k)+1][k]);
}
int p(int l, int r) {
if (l > r || l < 1 || r > n) return 0;
return std::min (100 * query_max (l, r), query_min (l, r));
}
int main() {
scanf ("%d%d", &n, &k);
for (int i=1; i<=n; ++i) {
scanf ("%d", &mx[i][0]);
}
build_max ();
for (int i=1; i<=n; ++i) {
scanf ("%d", &mn[i][0]);
}
build_min ();
for (int i=1; i<=n; ++i) {
int low = i, high = n;
while (low + 1 < high) {
int mid = low + high >> 1;
int v1 = 100 * query_max (i, mid);
int v2 = query_min (i, mid);
if (v1 < v2) low = mid;
else high = mid;
}
best[i-1] = std::max (p (i, low), p (i, high));
}
std::sort (best, best+n);
double prob = 1.0 * k / n;
double ans = prob * best[0];
for (int i=1; i<=n-k; ++i) {
prob = prob * (n - i - k + 1) / (n - i);
ans += prob * best[i];
}
printf ("%.12f\n", ans);
return 0;
}
题意:树上选择两条不相交的路径,且两条路径权值和最大.
分析:因为权值>0, 所以起点或终点一定在叶子结点上,第一次DFS,得到best[u]:u结点的子树下得到最大权值和(一条),以及down[u]:从结点u出发到叶子节点选择一条路的最大权值和.第二次DFS扫描每一个结点,从儿子中选择一个,它子树best[v1]作为一条路径,还有一条从前缀i以及后缀i+1中选择,更新最大值就是答案.
#include <bits/stdc++.h>
typedef long long ll;
const int N = 1e5 + 5;
std::vector<int> edge[N];
int a[N];
ll best[N], down[N];
ll ans;
int n;
void DFS(int u, int fa) {
std::vector<ll> downs;
for (auto v: edge[u]) {
if (v == fa) continue;
DFS (v, u);
best[u] = std::max (best[u], best[v]);
downs.push_back (down[v]);
}
ll mx1 = 0, mx2 = 0;
for (auto d: downs) {
if (d > mx1) {
mx2 = mx1; mx1 = d;
}
else if (d > mx2) {
mx2 = d;
}
}
best[u] = std::max (best[u], mx1 + mx2 + a[u]);
down[u] = mx1 + a[u];
ans = std::max (ans, best[u]);
}
void DFS2(int u, int fa, ll up) {
up += a[u];
std::vector<int> children;
for (auto v: edge[u]) {
if (v == fa) continue;
children.push_back (v);
}
int sz = children.size ();
if (sz == 0) return ;
std::vector<ll> prebest (sz + 1), sufbest (sz + 1); //前缀(1~i-1)最优的一条路径
prebest[0] = 0;
for (int i=0; i<sz; ++i) {
prebest[i+1] = std::max (prebest[i], best[children[i]]);
}
sufbest[sz] = 0;
for (int i=sz-1; i>=0; --i) { //后缀(i+1~sz-1)最优的一条路径
sufbest[i] = std::max (sufbest[i+1], best[children[i]]);
}
std::vector<ll> predown (sz + 1), predown2 (sz + 1); //前缀两条到叶子节点最优的路径
predown[0] = predown2[0] = 0;
for (int i=0; i<sz; ++i) {
predown[i+1] = predown[i];
predown2[i+1] = predown2[i];
ll x = down[children[i]];
if (x > predown[i+1]) {
predown2[i+1] = predown[i+1];
predown[i+1] = x;
}
else if (x > predown2[i+1]) {
predown2[i+1] = x;
}
}
std::vector<ll> sufdown (sz + 1), sufdown2 (sz + 1); //后缀两条到叶子节点最优的路径
sufdown[sz] = sufdown2[sz] = 0;
for (int i=sz-1; i>=0; --i) {
sufdown[i] = sufdown[i+1];
sufdown2[i] = sufdown2[i+1];
ll x = down[children[i]];
if (x > sufdown[i]) {
sufdown2[i] = sufdown[i];
sufdown[i] = x;
}
else if (x > sufdown2[i]) {
sufdown2[i] = x;
}
}
for (int i=0; i<sz; ++i) {
ll cur = std::max (prebest[i], sufbest[i+1]);
cur = std::max (cur, up + std::max (predown[i], sufdown[i+1]));
cur = std::max (cur, a[u] + predown[i] + sufdown[i+1]);
cur = std::max (cur, a[u] + predown[i] + predown2[i]);
cur = std::max (cur, a[u] + sufdown[i+1] + sufdown2[i+1]);
cur += best[children[i]];
ans = std::max (ans, cur);
}
for (int i=0; i<sz; ++i) {
int v = children[i];
ll new_up = up;
new_up = std::max (new_up, a[u] + std::max (predown[i], sufdown[i+1]));
DFS2 (v, u, new_up);
}
}
int main() {
scanf ("%d", &n);
for (int i=1; i<=n; ++i) scanf ("%d", a+i);
for (int u, v, i=1; i<n; ++i) {
scanf ("%d%d", &u, &v);
edge[u].push_back (v);
edge[v].push_back (u);
}
DFS (1, 0);
DFS2 (1, 0, 0);
printf ("%I64d\n", ans);
return 0;
}
DFS序 + 线段树 + bitset G - Yash And Trees
题意:两种操作; 1.v的子树的所有结点权值+x 2. 询问v子树%m后是素数的个数
分析:1操作想到线段树的成段更新,树变成线段用DFS序,每个结点有它'统治"的范围(子树). 然而后者统计用普通数组很难实现.用到了bitset这个容器,里面可以表示m位的01,本题表示一个结点子树所拥有的数值(%m),最后只要&primes就是素数个数.那么如何实现+x呢,因为每一位表示数值,往前一位表示+1,那么<<x, 还有可能移位超出去了,还要| >>(m - x).
#include <bits/stdc++.h>
#define lson l, mid, o << 1
#define rson mid + 1, r, o << 1 | 1
const int N = 1e5 + 5;
std::bitset<1000> tree[N<<2], primes, ret;
std::vector<int> edge[N];
int lazy[N<<2];
int a[N], id[N], fl[N], fr[N];
int n, m, q, tot;
void add(int &x, int y) {
x += y;
if (x >= m) x %= m;
}
void push_up(int o) {
tree[o] = tree[o<<1] | tree[o<<1|1];
}
void rotate(int o, int x) {
add (lazy[o], x);
tree[o] = (tree[o] << x) | (tree[o] >> (m - x));
}
void push_down(int o) {
if (lazy[o] != 0) {
rotate (o << 1, lazy[o]);
rotate (o << 1 | 1, lazy[o]);
lazy[o] = 0;
}
}
void build(int l, int r, int o) {
if (l == r) {
tree[o].set (a[id[l]]%m); return ;
}
int mid = l + r >> 1;
build (lson); build (rson);
push_up (o);
}
void updata(int ql, int qr, int x, int l, int r, int o) {
if (ql <= l && r <= qr) {
rotate (o, x); return ;
}
push_down (o);
int mid = l + r >> 1;
if (ql <= mid) updata (ql, qr, x, lson);
if (qr > mid) updata (ql, qr, x, rson);
push_up (o);
}
void query(int ql, int qr, int l, int r, int o) {
if (ql <= l && r <= qr) {
ret |= tree[o]; return ;
}
push_down (o);
int mid = l + r >> 1;
if (ql <= mid) query (ql, qr, lson);
if (qr > mid) query (ql, qr, rson);
}
void DFS(int u, int fa) {
id[fl[u]=++tot] = u;
for (auto v: edge[u]) {
if (v != fa) DFS (v, u);
}
fr[u] = tot;
}
bool is_prime(int x) {
if (x == 2 || x == 3) return true;
if (x % 6 != 1 && x % 6 != 5) return false;
for (int i=5; i*i<=x; i+=6) {
if (x % i == 0 || x % (i + 2) == 0) return false;
}
return true;
}
int main() {
scanf ("%d%d", &n, &m);
for (int i=1; i<=n; ++i) {
scanf ("%d", a+i);
}
for (int u, v, i=0; i<n-1; ++i) {
scanf ("%d%d", &u, &v);
edge[u].push_back (v);
edge[v].push_back (u);
}
tot = 0;
DFS (1, 0);
for (int i=2; i<m; ++i) {
if (is_prime (i)) primes.set (i);
}
build (1, n, 1);
scanf ("%d", &q);
while (q--) {
int op, v, x; scanf ("%d%d", &op, &v);
if (op == 1) {
scanf ("%d", &x);
x %= m;
updata (fl[v], fr[v], x, 1, n, 1);
}
else {
ret.reset ();
query (fl[v], fr[v], 1, n, 1);
ret &= primes;
printf ("%d\n", (int) ret.count ());
}
}
return 0;
}
暴力 || 莫队+线段树 H - Fibonacci-ish II
题意:q次询问,每次对l和r的范围内的数字去重,然后升序排序,计算fib[j] * a[j]的和．
分析：目前只会暴力的思路: 先排序, 然后每一个数原先对应的询问区间内累加，Ｏ(ｎｑ)复杂度险过
#include <bits/stdc++.h>
const int N = 3e4 + 5;
std::pair<int, int> a[N];
int fib[N];
int ql[N], qr[N], last[N], step[N];
int ans[N];
int main() {
int n, m; scanf ("%d%d", &n, &m);
for (int i=1; i<=n; ++i) {
scanf ("%d", &a[i].first);
a[i].second = i;
}
std::sort (a+1, a+1+n);
fib[0] = 1; fib[1] = 1;
for (int i=2; i<=n; ++i) fib[i] = (fib[i-2] + fib[i-1]) % m;
int q; scanf ("%d", &q);
for (int i=0; i<q; ++i) {
scanf ("%d%d", ql+i, qr+i);
last[i] = -1;
}
for (int i=1; i<=n; ++i) {
int v = a[i].first % m;
for (int j=0; j<q; ++j) {
if (a[i].second < ql[j] || a[i].second > qr[j]) continue;
if (a[i].first == last[j]) continue;
ans[j] = (ans[j] + v * fib[step[j]++]) % m;
last[j] = a[i].first;
}
}
for (int i=0; i<q; ++i) printf ("%d\n", ans[i]);
return 0;
}
编译人生，运行世界！
