POJ 2479
题意
找两个子区间的和的最大值,两个子区间不能相交。
解题思路
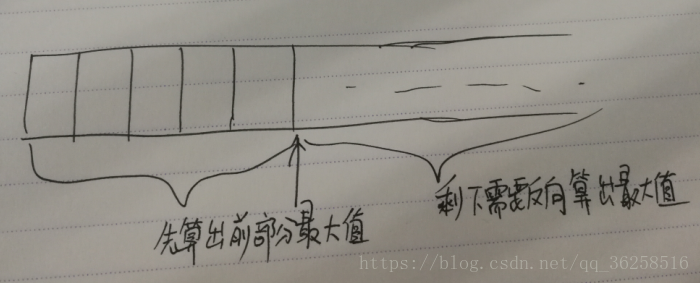
左一遍右一遍做两次最大子区间的和,存到两个数组中,最后枚举相邻,算出最大和。至于为什么这么写,画个图就很清楚了。
有人有可能要问为什么要反向算最大值?
因为如果依次枚举区间,直接算后半部分的最大值的话,就是O(n^2),妥妥的超时。所以这里只能用两个数组,分别从左右将所有区间的最大值存到相应的下标中,最后再错位枚举算出最大值即可。(PS:字有点丑,电子竞技没有书法)
代码
#include<stdio.h>
#include<iostream>
using namespace std;
#define inf 0x3f3f3f3f
#define maxn 50005
int arr[maxn],l[maxn],r[maxn];
int main()
{
// freopen("in.txt","r",stdin);
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
for(int i=0; i<n; i++)
scanf("%d",&arr[i]);
int sum=-inf,maxx=-inf;
for(int i=0; i<n; i++)
{
if(sum>0) sum+=arr[i];
else sum=arr[i];
maxx=max(maxx,sum);
l[i]=maxx;
}
sum=-inf,maxx=-inf;
for(int i=n-1; i>=0; i--)
{
if(sum>0) sum+=arr[i];
else sum=arr[i];
maxx=max(maxx,sum);
r[i]=maxx;
}
int ans=-inf;
for(int i=0;i<n-1;i++)
ans=max(l[i]+r[i+1],ans);
printf("%d\n",ans);
}
return 0;
}