注:参考KhanAcademy。
续(1)题目3:希尔排序、堆排序后面再补上。冒泡排序就不写了。
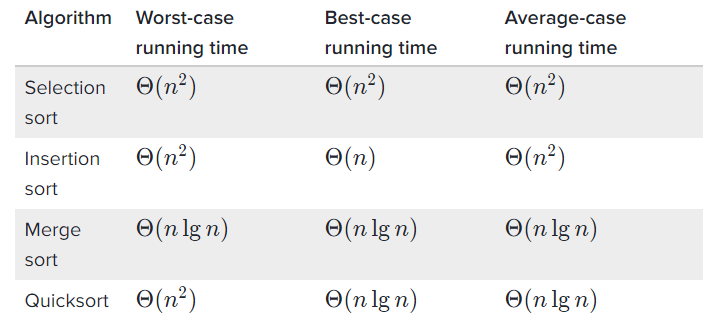
给一组整数,按照升序排序,使用选择排序,冒泡排序,插入排序或者任何 O(n2) 的排序算法。
插入排序(Insertion Sort)
(用插纸牌来理解很容易,每来一张新的牌,要插入到原来已经排好序的牌中。对于数组而言,中间插入一个新的元素,则右边本来的元素需要往右移动一个位置):
Algorithm:(从小到大)
1. curr = 1.(表示现在要插入的元素.[0, curr)为已经排好序的元素。)
2. key = array[curr], compare = curr-1; (要从[0, curr)最右的元素开始,一个个和key作比较。如果比key大,则要往右挪一个位置)
3. while(compare >= 0 AND key < array[compare]): {array[compare+1] = array[compare]; compare--;}
4. array[compare+1] = key. (最后所有元素都比较完了,或是compare上的元素比key要小,那么就在数组头部插入(此时compare = -1),或者插入到compare元素的后面)
5. while(curr < len(array)): {curr++; go back to step 2;} (遍历所有元素,逐个插入)
复杂度:
- Worst case: $\Theta(n^2)$2)
- Best case: $\Theta(n)$
- Average case for a random array: $\Theta(n^2)$)
- "Almost sorted" case: $\Theta(n)$
Python:
#!/usr/bin/python def insertV(array, rightIndex, key): for comp in range(rightIndex, -1, -1): if array[comp] > key: array[comp+1] = array[comp] else: array[comp+1] = key break if array[0] > key: array[0] = key def InsertionSort(array): for curr in range(1, len(array)): insertV(array, curr-1, array[curr]) #print(array) testArray = [1, 0, 3, -1, 3, 6, 2] InsertionSort(testArray)
C++:
#include <iostream> using namespace std; void insert(int array[], int rightIndex, int value){ int comp; for(comp = rightIndex; (comp >=0) && (array[comp] > value); comp--){ array[comp+1] = array[comp]; } array[comp+1] = value; } void insertionSort(int array[], int len){ for(int curr = 1; curr < len; curr++){ insert(array, curr-1, array[curr]); } } int main() { int testArray[] = {1, 3, 0, -1, 2, 8}; int len = sizeof(testArray)/sizeof(testArray[0]); insertionSort(testArray, len); for(int i = 0; i < len; i++){ cout << *(testArray+i) << " "; } return 0; }
Javascript:
var insert = function(array, rightIndex, value) { var curr; for(curr = rightIndex; curr >= 0 && array[curr] > value; curr--){ array[curr+1] = array[curr]; } array[curr+1] = value; }; var insertionSort = function(array) { for(var curr = 1; curr < array.length; curr++){ insert(array, curr-1, array[curr]); } };
快速排序(Quick Sort)
(简要思想):
利用分治法,选择一个基准元素,将序列中大于、小于该元素的元素分别归置到两边,并对这两个部分分别递归地进行相同的操作,直到元素个数小于2。
选取基准元素的方法有多种,下面的算法在每一步里选取序列最右的元素作为基准。如果是大于基准的,放到右边;小于基准的,放到左边。
下图中,黄色标记的元素为基准元素,蓝色表示小于基准的,红色表示大于基准的(对于与基准相等的情况,可定义归为蓝色的,也可定义归为红色的,整个算法是统一的即可)。
当进行一次划分以后,基准元素indP的位置就确定为蓝色区域的右侧第一位,同时也是红色区域的左侧第一位,后面再分别递归地对蓝色、红色部分做排序时,该基准元素的位置不再发生变化,在这里用黑色表示。而当划分得到的蓝色或红色区域只含一个元素或不含元素时,不必再做递归操作,其位置也已经确定,故而也置为黑色。
具体的,将元素划分为大于、小于基准两个部分的操作,是通过元素逐个和基准进行大小比较,并进行部分交换完成的。
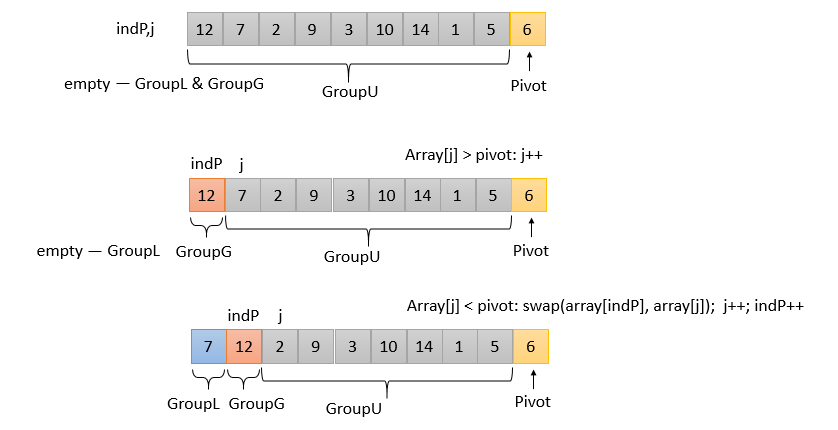
下图是一个具体的展示,Pivot为基准元素,选取的是序列的最右元素。
其中GroupL,GroupG分别表示小于基准Pivot的元素集合、大于或等于基准Pivot的元素集合;GroupU表示未进行比较的元素集合;
indP表示Pivot最终所在的位置;j表示未比较元素中最左那一个的下标。
GroupL、GroupG一开始都为空,而GroupU包括了除了Pivot的所有元素。indP和j一开始都等于左边第一个元素的下标start。
从GroupU最左的元素开始,每个元素和Pivot进行比较,
GroupL和GroupG不断扩充(也可能有其中一个不会),GroupU元素不断被消耗,indP逐步接近最终的位置:
(在将Pivot进行最后一步交换前,[start,indP)的区域为GroupL;[indP,j)的区域即为GroupG。之后把indP上的元素和Pivot交换,划分才完成。)
若
1. array[j] >= Pivot,则这个元素属于GroupG;indP不变,因为indP是要落在GroupL的右侧第一位的;j增加1,指向下一个元素;
2. array[j] < Pivot,则这个元素属于GroupL,将indP上的元素和j上的元素交换,以使GroupL的元素落在GroupG左边;indP增加1;j增加1,指向下一个元素。
直到GroupU元素消耗完,也即j=end,将pivot和indP上的元素交换,返回indP因为后面递归的调用需要根据indP来确定。
(经过这些步骤,GroupG中元素的顺序会和原序列的相反,上一张图只做示意,没有考虑这个细节。)

Algorithm(从小到大):
Divide:对于序列array[start,...,end],令Pivot = array[end],然后将array根据元素与Pivot的相对大小进行划分,得到array[start,...,indP-1],Pivot, array[indP+1, ..., end]。
Conquer:若indP-1>start, 递归地对array[start, ..., indP-1]进行Divide&Conquer;
若end > indP+1,递归地对array[indP+1, ..., end]进行Divide&Conquer。
Combine:无须额外操作,在divide中已经对元素位置依据元素大小进行调整。
划分(Partition)步骤:
1. indP, j = start, Pivot = array[end]
2. for j < end:
if array[j] >= Pivot: j++ (“=”合在array[j] < Pivot处也是可以的)
if array[j] < Pivot; 交换array中j和indP指向的元素的值:swap(array, j, indP);indP++; j++
3. 将Pivot放置到indP,即进行end和indP指向元素的交换:swap(array, end, indP).
4. return indP
算法复杂度:
划分n元素序列的时间复杂度为$\Theta(n)$(每个元素都会和基准元素进行1次比较;交换至多进行1次:3次赋值;j和indP至多进行1次赋值),这个部分花费的时间是稳定的;
但基准元素的选取会影响到需要进行多少次划分:
1. 最好的情况:每次都把序列二等分,则需要做$\log_2 n$次划分,为$\Theta(\log n)$;
2. 最坏的情况:每次划分选中的基准元素都是序列里的最大或者最小值,序列被划分为1:0,则需要做$n$次划分,为$\Theta(n)$;
3. 一般情况:以每次划分都把序列划分为1:3的情况为例,则需要做$\log _{4/3} n$次划分,为$\Theta(\log n)$。即便是划分为1:3和划分为1:0的情况交叉出现,也只需要$2* \log_{4/3} n$次划分,同样为$\Theta(\log n)$。这并不是严格的证明一般情况的时间复杂度为$\Theta(\log n)$,只是直观上可以促进理解。
划分的次数和划分的复杂度乘起来则是整个算法的复杂度:
1. 最好:$\Theta(n \log n)$
2. 最坏:$\Theta(n^2)$
3. 一般:$\Theta(n \log n)$
为了改进算法的时间复杂度,有时也采取随机选取基准元素的做法,当然和选取最右、最左的元素作为基准的做法相比时间究竟是否节省了,在不同的例子中有不同的答案,这个改进更多的是为了避免最坏情况的发生;
还有另一种改进方法是每次选择3个或更多的参考值,以其中位数作为基准。这个方法确实能有效降低划分的次数,且参考值越多降低的次数越多;但同时,选择参考值(如果随机)和计算中位数也是需要花费时间的,并且这个时间会随着参考值个数增加而增加,所以参考值个数也不宜过多。
Javascript:
// Swaps two items in an array, changing the original array var swap = function(array, firstIndex, secondIndex) { var temp = array[firstIndex]; array[firstIndex] = array[secondIndex]; array[secondIndex] = temp; }; var partition = function(array, p, r) { // Compare array[j] with array[r], for j = p, p+1,...r-1 // maintaining that: // array[p..q-1] are values known to be <= to array[r] // array[q..j-1] are values known to be > array[r] // array[j..r-1] haven't been compared with array[r] // If array[j] > array[r], just increment j. // If array[j] <= array[r], swap array[j] with array[q], // increment q, and increment j. // Once all elements in array[p..r-1] // have been compared with array[r], // swap array[r] with array[q], and return q. var q = p; for(var j = p; j < r; j++){ if(array[j] <= array[r]){ swap(array, j, q); q++; } } swap(array, q, r); return q; }; // If the subarray has size 0 or 1, then it's already sorted, and so nothing needs to be done. // Otherwise, quickSort uses divide-and-conquer to sort the subarray. var quickSort = function(array, p, r) { if(p < r){ var curr = partition(array, p, r); quickSort(array, p, curr-1); quickSort(array, curr+1, r); } };
Python:
def swap(array, ind1, ind2): temp = array[ind1] array[ind1] = array[ind2] array[ind2] = temp def partition(array, start, end): pivot = array[end] indP = start for j in range(start, end): # j increases every step if array[j] < pivot: swap(array, j, indP) # array[j] belongs to GroupL, the left part indP += 1 swap(array, end, indP) return indP def quickSort(array, start, end): indP = partition(array, start, end) if indP-1 > start: quickSort(array, start, indP-1) if end > indP+1: quickSort(array, indP+1, end) testNum = [0, 9, -10, -3, 5, 2, 0] quickSort(testNum, 0, len(testNum)-1) print(testNum)
归并排序(Merge Sort)
(简要思想):
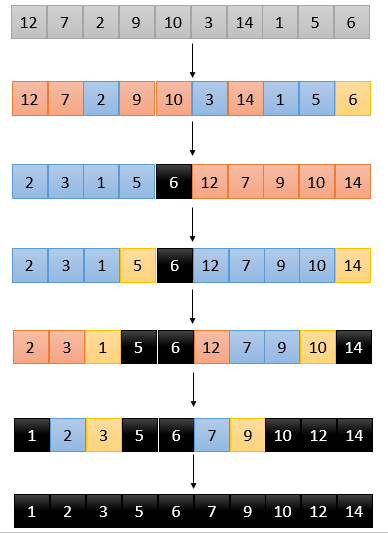
将要排序的序列拆分成两个小序列,对这两个小序列进行排序后再合并排序;而这两个小序列的排序方法,和原序列是相同的,同样是拆分、再对子序列排序、再合并排序。
实际上,在这个过程中出现的每一个长度大于1的序列,都经历这样的过程,直到序列只含一个元素。
举个例子:
原序列:[1, 4, 0, 6]
拆分为[1,4], [0,6],则需要对[1,4]和[0,6]分别进行排序,然后合并排序;
两个子序列各自的排序:[1,4]拆分为[1]、[4];[0,6]拆分为[0]、[6]。由于现在的序列都只含有一个元素,所以递归到底,进入各自的合并操作:[1]和[4]合并排序得到[1,4];[0]和[6]合并排序得到[0,6];
两个子序列的合并排序:[1,4]和[0,6]合并排序,得到[0,1,4,6]。
结束。
那么剩下的,就是要定义合并排序的方法。一般采用的是复杂度为$\Theta(n)$的排序方法:
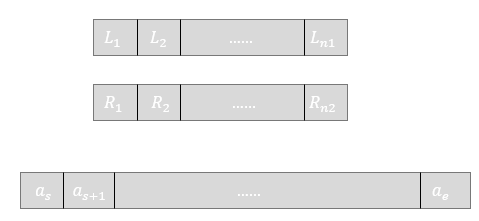
如图,等待合并排序的为$a_s, a_{s+1}, \cdots, a_e$,其中将序列划分为两边的端点为$a_{mid}$,
将$a_s, a_{s+1}, \cdots, a_{mid}$和$a_{mid+1}, a_{mid+2}, \cdots, a_e$分别复制到$L$和$R$两个新数组中。
因为$L$和$R$都经过排序,所以各自最小的值都在最左,则第一次插入值时,只需要比较$L_1$和$R_1$的大小,如果$L_1 \leq R_1$,则将$a_s$的值变更为$L_1$;
而后$L$和$R$中未插入到原序列的值的最小值仍然出现在最左,如果前面插入的是$L_1$,则目前各自的最小值则为$L_2$、$R_1$,因此仍然只需要比较两个元素。往后的每一步比较插入,显然都只需要比较两个元素即可。
如果到了某一步,其中一个序列的值已经用完,那么剩下那个序列把剩余的部分直接填充进去即可。
在这个过程中,每次插入进行两个数的比较,假设序列长度为$n$,则共进行了$n$次插入,同时$n$次比较,每个数被比较的次数不超过2,因而复杂度为$\Theta(n)$.
(这里只介绍了递归的解法。也可以不用递归,直接对相邻的最小序列(长度为1)合并排序,再对长度为2的相邻序列合并排序,直到合并为一个序列,可参考静默虚空的写法)
Algorithm(从小到大):
Divide:对于一个序列$[a_1, a_2, \cdots, a_n]$,将其分为两半,现在start = 0, end = n-1,另mid = floor((start+end)/2)。(当然也可以规定向上取整)
$Left = [a_{start}, a_{start+1}, \cdots, a_{mid}]$, $Right = [a_{mid+1}, a_{mid+2}, \cdots, a_{end}]$
Conquer:如果Left或Right只剩一个元素,那么不用再Divide,直接返回自身;否则递归地解决Left的排序;递归地解决Right的排序(对Left和Right继续分别Divide和Conquer)。
Combine:将Left和Right合起来排序。
合并排序:
(用curr、indL、indR分别来表示在原序列,左序列和右序列中未进行比较、插入的第一个元素)
curr = s; indL = 0; indR = 0;
(如果下标超过数组长度,说明都插入好了,或者是有一个数组用完了,另一个数组剩下的元素都会比已经插入的元素要大)
while (indL < mid-s+1) & (indR < e-mid):
if Left[indL] < Right[indR]: indL++; a[curr] = Left[indL];
else indR++; a[curr] = Right[indR];
curr++;
(有一个数组用完,但是插入还没有完成,那剩下的就不用再比较了)
if (indL == mid-s+1) & (curr < e): (或者indR < e-mid)
a[curr, ..., e] = Right[indR, ...]
if (indR == e-mid) & (curr < e): (或者indL < mid-s+1)
a[curr, ..., e] = Left[indL, ...]
复杂度:
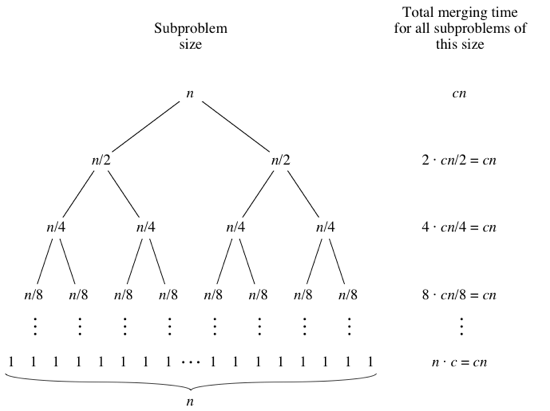
Divide和Conquer的部分,每次做中间点计算、复制数组、调用自身函数、合并排序四部分。前三部分均花费$\Theta(1)$,而合并排序花费的时间如下图所示。
由于在树的每一层,调用mergesort函数的次数不会超过$n$,所以树的每一层花费的时间仍然被某一个常数$c \ast$控制在$c\ast n$以下,因此依旧是$\Theta(n)$的。
总的时间花费,为每一层的时间乘以树的层数$L$,而$L \leq \lg n +1$,从而总的时间花费为$\Theta(n \log n)$的。
但和选择排序、插入排序不同的是,归并排序中需要对数组进行复制,空间复杂度更高。
Javascript:
// Takes in an array that has two sorted subarrays, // from [p..q] and [q+1..r], and merges the array var merge = function(array, p, q, r) { var lowHalf = []; var highHalf = []; var k = p; var i; var j; for (i = 0; k <= q; i++, k++) { lowHalf[i] = array[k]; } for (j = 0; k <= r; j++, k++) { highHalf[j] = array[k]; } k = p; i = 0; j = 0; // Repeatedly compare the lowest untaken element in // lowHalf with the lowest untaken element in highHalf // and copy the lower of the two back into array while(i < lowHalf.length && j < highHalf.length){ if(lowHalf[i] < highHalf[j]){ array[k] = lowHalf[i]; i++; }else{ array[k] = highHalf[j]; j++; } k++; } // Once one of lowHalf and highHalf has been fully copied // back into array, copy the remaining elements from the // other temporary array back into the array while(i < lowHalf.length){ array[k] = lowHalf[i]; i++; k++; } while(j < highHalf.length){ array[k] = highHalf[j]; j++; k++; } }; // Takes in an array and recursively merge sorts it var mergeSort = function(array, p, r) { if(r === p){ return 0; } if(p !== r){ var mid = floor((p+r)/2); mergeSort(array, p, mid); mergeSort(array, mid+1, r); merge(array, p, mid, r); } };
Python:
import math # to merge to parts of the array def merge(array, start, mid, end): Left = array[start:(mid+1)] Right = array[(mid+1):(end+1)] indL = 0 indR = 0 curr = start # Repeatedly compare the lowest untaken element in # lowHalf with the lowest untaken element in highHalf # and copy the lower of the two back into array while (indL < len(Left)) & (indR < len(Right)): if Left[indL] < Right[indR]: array[curr] = Left[indL] indL += 1 else: array[curr] = Right[indR] indR += 1 curr += 1 # Once one of lowHalf and highHalf has been fully copied # back into array, copy the remaining elements from the # other temporary array back into the array if indL < len(Left): array[curr:(end+1)] = Left[indL:] if indR < len(Right): array[curr:(end+1)] = Right[indR:] # recursive divide and call itself and then merge def mergeSort(array, start, end): if start == end: return 0 else: mid = math.floor((start+end)/2) mergeSort(array, start, mid) mergeSort(array, mid+1, end) merge(array, start, mid, end) testNum = [0, 9, -1, 3, 5, 2] mergeSort(testNum, 0, len(testNum)-1) print(testNum)



