Deep Learning 学习笔记（9）：主成分分析( PCA )与 白化( whitening )

废话：

这博客有三个月没更新了。

三个月！！！尼玛我真是够懒了！！

这三个月我复习什么去了呢？

托福…………

也不是说我复习紧张到完全没时间更新，

事实上我甚至有时间打LOL。

只是说，我一次就只能（只想？）做一件事情。

对我来说，在两种不同思维之间转换是十分耗费能量的。

说白了我！就！是！个！废！柴！……哼……

前言：

PCA与白化，

就是对输入数据进行预处理，

前者对数据进行降维，后者对数据进行方差处理。

虽说原理挺简单，但是作用可不小。

之前的师兄做实验的时候，就是忘了对数据预处理，

结果实验失败了。

可见好的PCA对实验结果影响挺重要。

主成成分分析（PCA）：

 

主要思想（我总结的）：

通过抛弃携带信息量较少的维度对数据进行降维处理，从而加速机器学习进程。

 

方法：

一、数据的旋转（其实我觉着，这个有点像向量正交化的过程）

1、使用的输入数据集表示为 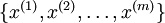\textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\}

2、首先计算出协方差矩阵 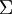\textstyle \Sigma ，如下所示：

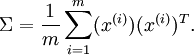
\begin{align} \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. \end{align}

可以证明，数据变化的主方向 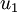\textstyle u_1 就是协方差矩阵 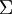\textstyle \Sigma 的主特征向量，而 变化的次方向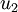\textstyle u_2 是次特征向量，以此类推。

（证明略，事实上如果只是想实现算法这个定理不用理解。但我已决定重修线代（By Myself），因为越到后面越发现线性代数的重要性。）

3、我们可以通过matlab或其他线代软件求解出协方差矩阵的特征向量，并按列排列如下：

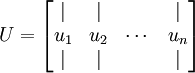
\begin{align} U = \begin{bmatrix} | & | & & | \\ u_1 & u_2 & \cdots & u_n \\ | & | & & | \end{bmatrix} \end{align}

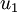      \textstyle u_1 是主特征向量（对应最大的特征值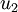）， \textstyle u_2 是次特征向量。以此类推，另记 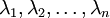\textstyle \lambda_1, \lambda_2, \ldots, \lambda_n 为相应的特征值（数值递减）。

4、旋转数据。向量  构成了一个新基，可以用来表示数据。令 为训练样本，那么  就是样本点 i 在维度 上的投影的长度（幅值）。

 

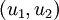     至此，以二位空间为例，我们可以把 \textstyle x 用 \textstyle (u_1, u_2) 基表达为：

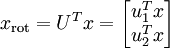
\begin{align} x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^Tx \\ u_2^Tx \end{bmatrix} \end{align}

   

     引用UFDL两张图

     可见变化最大的维度（携带信息最多，在我们EE人的眼中，交流能量（方差）可以用来表征信号的信息）被排到了最前。

旋转前 旋转后
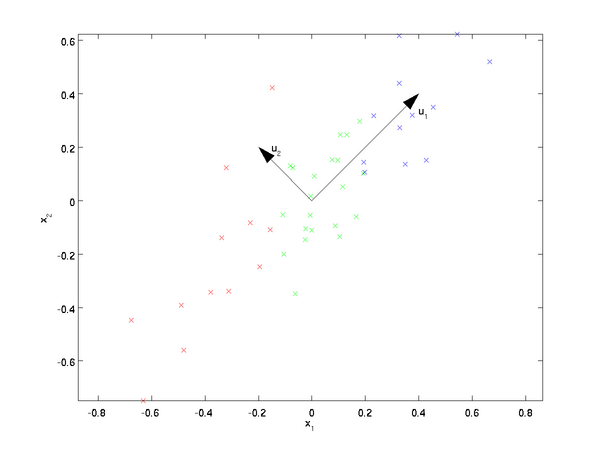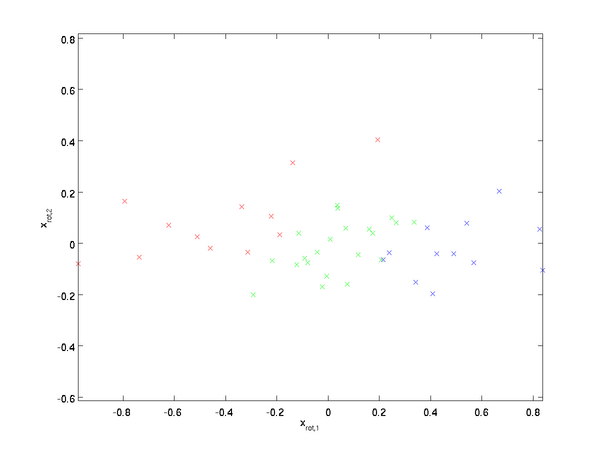PCA-u1.png PCA-rotated.png

 

 

 

二、数据的取舍

接上，我们用方差来表征一个信号的信息，在旋转过后的数据中，我们把最后面方差较小的维度舍去。

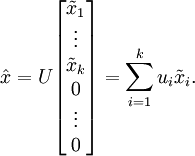
\begin{align} \hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^k u_i \tilde{x}_i. \end{align}

保留下来的数据与原数据所携带的信息比为

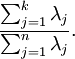
\begin{align} \frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j}. \end{align}

一般取

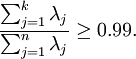
\begin{align} \frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j} \geq 0.99. \end{align}

（若向他人介绍PCA算法详情，告诉他们你选择的 \textstyle k 保留了99%的方差）

总的来说，PCA后，数据的近似表示

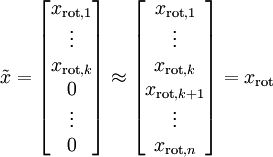
\begin{align} \tilde{x} = \begin{bmatrix} x_{{\rm rot},1} \\ \vdots \\ x_{{\rm rot},k} \\ 0 \\ \vdots \\ 0 \\ \end{bmatrix} \approx \begin{bmatrix} x_{{\rm rot},1} \\ \vdots \\ x_{{\rm rot},k} \\ x_{{\rm rot},k+1} \\ \vdots \\ x_{{\rm rot},n} \end{bmatrix} = x_{\rm rot} \end{align}

即，我们舍去n维向量中的(n-k)维，用k维向量来表示数据，可见数据的维度被缩小了。

 

如，舍去第二维之后的数据

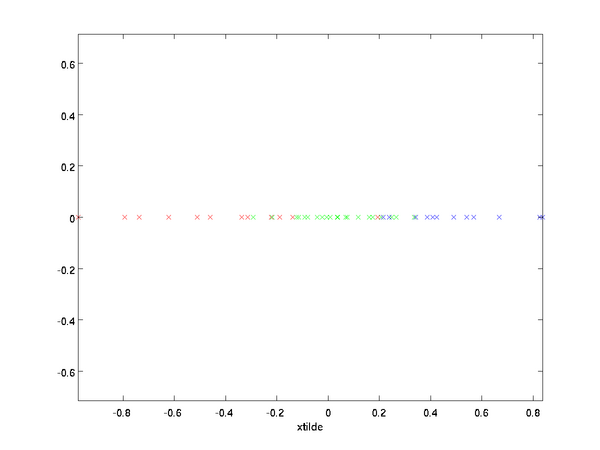
PCA-xtilde.png

 

三、复原

其实一般都不复原，那么辛苦排除了无用信息还复原干蛋。只是说有这么个东西……

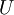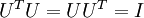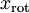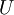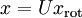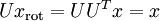矩阵 \textstyle U 有正交性，即满足 \textstyle U^TU = UU^T = I ，所以若想将旋转后的向量 \textstyle x_{\rm rot} 还原为原始数据 \textstyle x ，将其左乘矩阵\textstyle U即可： \textstyle x=U x_{\rm rot} , 验算一下： \textstyle U x_{\rm rot} = UU^T x = x，即：

\begin{align} \tilde{x} = \begin{bmatrix} x_{{\rm rot},1} \\ \vdots \\ x_{{\rm rot},k} \\ 0 \\ \vdots \\ 0 \\ \end{bmatrix} \approx \begin{bmatrix} x_{{\rm rot},1} \\ \vdots \\ x_{{\rm rot},k} \\ x_{{\rm rot},k+1} \\ \vdots \\ x_{{\rm rot},n} \end{bmatrix} = x_{\rm rot} \end{align}

 

 

白化（Whitening）:

　　主要思想（教程上的）：

　　由于图像中相邻像素之间具有很强的相关性，所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性；更正式的说，我们希望通过白化过程使得学习算法的输入具有如下性质：(i)特征之间相关性较低；(ii)所有特征具有相同的方差。

 

  方法：　　　

　　在上一步PCA中，旋转过后的维度间已经不具有相关性（果真正交化？）。因此这里只用将数据的方差化为一即可。

　　可知协方差矩阵对角元素的值为 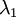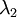\textstyle \lambda_1 ，\textstyle \lambda_2 ……为数据方差，方差归一：

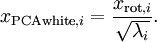
　　　　　　　　　　　　　　　　　　　                 　\begin{align} x_{{\rm PCAwhite},i} = \frac{x_{{\rm rot},i} }{\sqrt{\lambda_i}}. \end{align}

 

　　（对，就这么就完了，当然这只是最最最简单的东西）

 

TIPS：

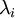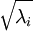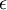　　未防止 \textstyle \lambda_i 过于接近零，这样在缩放步骤时我们除以 \sqrt{\lambda_i} 将导致除以一个接近0的值；这可能使数据上溢 。因而在实践中，我们使用少量的正则化实现这个缩放过程，即在取平方根和倒数之前给特征值加上一个很小的常数 \textstyle \epsilon：

\begin{align} x_{{\rm PCAwhite},i} = \frac{x_{{\rm rot},i} }{\sqrt{\lambda_i + \epsilon}}. \end{align}

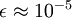　　当 \textstyle x 在区间 \textstyle [-1,1] 上时, 一般取值为 \textstyle \epsilon \approx 10^{-5}。

（教程上是这么说的，但是事实上我认为如果某一维度的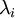\textstyle \lambda_i过于接近零，这个维度在PCA过程中将会被舍弃。可能教程中针对的是未经过PCA的数据即：ZCAWhite？）

 

 

完结：？

基本上把几个月的深度学习自己过了一遍（虽然有相当一部分是复制粘贴的0）。

后面的池化和卷积就不写了，能用到的不多。

至于稀疏编码写不写，还要看学不学。

因为在UFLDL里面这方面的内容还未完善，

而且稀疏编码的激活函数都是可学习的，

不仅理解难度大，实现起来难度也大。

师兄学习的时候跑了两天………………何况我的I3-M一代。

暂且就这样吧。

 

接下来想学习python和theano，

提高应用能力，

然后向自己找点资料搞实验。（事实上已经找到）

不过需要指导老师，和老师打交道什么的最不懂了。

 

自学DL后深深感到线性代数知识的匮乏，需要恶补。

同时发现这个是DL因为可并行计算很多，很有硬件加速的前途（FPGA？不过矩阵运算好像还不成熟？）。

要是做成芯片肯定很有前途啊~

 

管他呢！

 

posted @ 2013-11-17 23:31  Pony_s  阅读(15114)  评论(1)  编辑  收藏  举报