动态规划---等和的分隔子集（计蒜课）、从一个小白的角度剖析DP问题

自己还是太菜了，算法还是很难。。。这么简单的题目竟然花费了我很多时间。。。在这里我用一个小白的角度剖析一下这道题目。

 

晓萌希望将1到N的连续整数组成的集合划分成两个子集合，且保证每个集合的数字和是相等。例如，对于N=3，对应的集合{1，2，3}能被划分成{3} 和 {1,2}两个子集合.

这两个子集合中元素分别的和是相等的。

对于N=3，我们只有一种划分方法，而对于N=7时，我们将有4种划分的方案。

输入包括一行，仅一个整数，表示N的值（1≤N≤39）。

输出包括一行，仅一个整数，晓萌可以划分对应N的集合的方案的个数。当没发划分时，输出0。

样例输入

7

样例输出

　　

4

为了做出来这道题目我看了很多博客，发现很多人用一维的方法去处理这道题目，不过鉴于我太菜了。。。所以还是用二维去理解然后做题吧，，
这道题目关键点在于发现大问题可以归于小问题的求解，在分析这道题目的时候，我们能发现问题可以抽象成01背包问题，即：第i个数要还是不要的问题。
也就是说我的一个大问题可以分解成两个子问题：①当现在考虑的物品范围是1~i-1的时候，我们的背包容量已经达到了j，这时候我们不要第i个物品（抽象成这道题目就是：当我们不要第i个数时，我们前i-1个数中已经有满足相加为j的组合）
②考虑范围也是1~i-1，这个时候我们要将第i个物品放到背包中，也就是说我们要使用数组DP[i-1][j-i]存的数据（在这里我要稍微解释一下这个DP[][]数组的含义：第一个维度表示我们现在考虑的是1~i个数，然后第二维度表示我的背包最多存储的值的大小），在这里我们可以这么理解：就是我如果在包里放入第i个数，那就意味着我如果要让最后数的总和达到j，那就要调用j-i这个里面的数据。

上面的分析有可能有点混乱，但是总结一点，那就是我DP[i][j]里面的数据是有前面已经生成的两个数据组成：DP[i][j]=DP[i-1][j]+DP[i-1][j-1]。


下面换一个解释方法：（如果已经懂了的可以跳过）

为避免词语重复，下面说S中第i个元素时，就是指第i个整数。

       假设此时，S中前i-1个元素都判断完了，紧接着应该判断第i个元素，与此同时，子集合的整数和被限定为sum，那么这第i个元素要不要被加入子集合呢？对此，我们做如下推断：

           1：如果这第i个元素本身大于子集合的整数和sum，即i>sum，那么这第i个元素肯定不能加入子集合，否则就超出子集合整数和限制了。此时：F(i, sum)=F(i-1, sum)，意思就是在相等的子集合整数和限制下，既然第i个元素没被加入，那么判断完第i个元素后的整数选取方案与判断完第i-1个数时的方案应该是相同的。

           2：如果这第i个元素小于子集合整数和，那么就有两种考虑：

                2.1：坚持不把第i个元素放入子集合，那么此时整数的选取方案仍然有F(i-1, sum)种。

                2.2：如果把第i个元素放入了子集合，那么此时整数的选取方案有F(i-1, sum-i)种，sum-i的含义在于既然要放入第i个元素，就要给它留下足够的空间。F(i-1, sum-i)是在肯定要放入元素i的情形下，放入元素i前，整数的选取方案。

           也即是说，i<=sum时，F(i, sum)=F(i-1, sum)+F(i-1, sum-i)。

           综上可得：

   

 

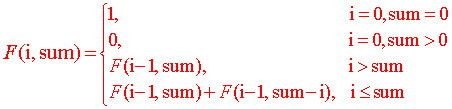
这个就是DP问题的关键部分的函数，剩下的步骤就是付给初值然后动态赋值。

#include<iostream>
using namespace std;
    long long DP[50][5000];//里面放的是情况数，注意类型，我就是因为类型被wa了好多次。。。。。
int main(){
    
    
    int n;
    cin>>n;
    int s=(1+n)*n/2;
    
    if(s%2==1) {
    cout<<0;return 0;}//这个是判断是否能够分成两组，因为每一组的值都是总和的一半，所以总和必须是偶数。
    int ss = s/2;

    DP[0][0]=1;//这个就是关键的初值：当我背包的重量为0时，考虑前0个数，也就是把0放到包里这一种情况，所以情况数为1.
    
    for(int i=1;i<=ss;i++){
        DP[0][i] = 0;//当我背包容量为i时（i>0），这个时候在前0个数中无法找到任何组能满足我的这个需求，所以为0.
    }
    for(int i=1;i<=n;i++){
        for(int h=0;h<=ss;h++){
            if(h<i) DP[i][h]=DP[i-1][h];//当h<i时，意味着背包需求为h，但是我i已经大于h了，意味着肯定不能把i放进背包，所以当前情况为上一种情况。
            else{
                DP[i][h]=DP[i-1][h]+DP[i-1][h-i];//这就是那个动态方程（上面内容已经讲了）
            }
        }
    }
    cout<<DP[n][ss]/2<<endl;//输出的时候要/2。因为我的里面分成了两组，得出的结果是有一半其实属于同一个情况的
    
    
    
    
}

 

在这里放上代码。

动态规划确实不太好理解，以后还是多写题目吧。。。太菜了
Orz。。。


----------------------------------------------------------------------------------Made By 蒟蒻 Pinging。。