Greedy:Fence Repair（POJ 3252）

　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　Fence Repair

　　问题大意：农夫约翰为了修理栅栏，要将一块很长的木块切割成N块，准备切成的木板的长度为L1，L2...LN，未切割前的木板的长度恰好为切割后木板的长度的总和，每次切断木板的时候，需要的开销为这块木板的长度，例如长度为21的木板需要切成长度为5,8,8的三块木板，长为21的木板切成长为13和8的板时，开销为21,。再将长度为13的板切成长度为5和8的板时，开销是13，于是合计开销是34，然后要你求切割完的最小开销是什么。

 

　　乍眼看这一道题好像有很多种切割方案，似乎是很难解决的，但是我们这样想，就是当我们切一块木板的时候，我们所用的开销就是切割这一块木板所要用到的长度，我们得到了两块木板，这两块木板可以继续切的话，他们的总开销就是这两块木板的和，也就是一块长的木板。那么我们想到最后，就会发现其实就是我们得到了一个这样的东西，就是最小的板会所要用到的开销会占N次（视通过多少次分割得到这块板来定），如果我们要画一幅图来展示这个过程的话。。。

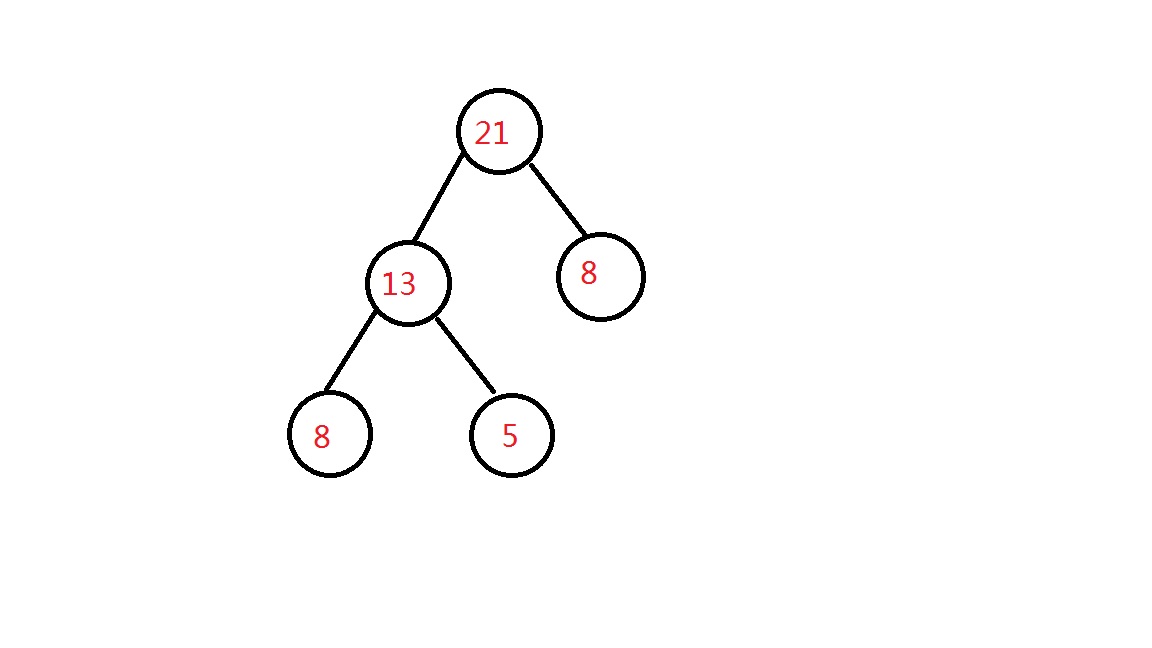
　　上面最大的开销是34=8*2+5*2+8（也就是二叉树的树叶对应节点大小乘以高度）

　　那么为了得到最小的开销，我们很容易就发现，我们只要把相对较小的节点放在比较深的地方就可以了，这是一种比较常用的贪婪的思想，证明我就省略了

那么现在我们只用不断地把最小的节点结合起来，最后就会形成最小的开销，那么不断找最小嘛，很容易就想到用堆，堆呢你可以自己写（熟练的话会很快），也可以直接用std（会比较简洁）

 

 1 #include<stdio.h>
 2 #include<stdlib.h>
 3 
 4 typedef int Position, *Heap;
 5 
 6 int Delete_Min(Heap, int *const);
 7 void Push(Heap, int, int *const);
 8 
 9 int main(void)
10 {
11     int N, i, size = 0;
12     int L1, L2, tmp;
13     long long ans = 0;
14 
15     while (~scanf("%d",&N))
16     {
17         Heap pque = (Heap)malloc(sizeof(int)*N);
18         for (i = 0; i < N; i++)
19         {
20             scanf("%d", &tmp);
21             Push(pque, tmp, &size);
22         }
23         while (size > 1)
24         {
25             L1 = Delete_Min(pque, &size);
26             L2 = Delete_Min(pque, &size);
27 
28             ans += (long long)L1 + L2;
29             Push(pque, L1 + L2, &size);
30         }
31         free(pque);
32         printf("%lld\n", ans);
33     }
34 }
35 
36 int Delete_Min(Heap heap,int *const size)
37 {
38     Position pr = 1, s1, s2, s;
39     int out = heap[1], tmp = heap[(*size)--];
40     for (; pr <= *size;)
41     {
42         s1 = pr << 1; s2 = s1 + 1;
43         if (s2 <= *size)
44         {
45             if (heap[s1] < heap[s2]){ heap[pr] = heap[s1]; pr = s1; }
46             else{ heap[pr] = heap[s2]; pr = s2; }
47         }
48         else
49         {
50             if (s1 <= *size){ heap[pr] = heap[s1]; pr = s1;break; }
51             else break;
52         }
53     }
54     for (s = pr; s > 1;)
55     {
56         if (s % 2 == 0)
57         {
58             pr = s >> 1;
59             if (heap[pr] > tmp) { heap[s] = heap[pr];s = pr;}
60             else break;
61         }
62         else
63         {
64             pr = (s - 1) >> 1;
65             if (heap[pr] > tmp){ heap[s] = heap[pr];s = pr; }
66             else break;
67         }
68     }
69     heap[s] = tmp;
70     return out;
71 }
72 
73 void Push(Heap heap, int item, int *const size)
74 {
75     Position s = ++(*size), pr;
76     for (; s > 1;)
77     {
78         if (s % 2 == 0)
79         {
80             pr = s >> 1;
81             if (heap[pr] > item) { heap[s] = heap[pr]; s = pr; }
82             else break;
83         }
84         else
85         {
86             pr = (s - 1) >> 1;
87             if (heap[pr] > item){ heap[s] = heap[pr]; s = pr; }
88             else break;
89         }
90     }
91     heap[s] = item;
92 }

这是直接写堆的代码

 1 #include<iostream>
 2 #include<queue>
 3 #include<functional>
 4 #include<cstdio>
 5 
 6 using namespace std;
 7 
 8 int main(void)
 9 {
10     int N, i;
11     int L1, L2, tmp;
12     long long ans = 0;
13 
14     while (~scanf("%d", &N))
15     {
16         priority_queue<int, vector<int>, greater<int> >pque;
17         for (i = 0; i < N; i++)
18         {
19             scanf("%d", &tmp);
20             pque.push(tmp);
21         }
22         while (pque.size() > 1)
23         {
24             L1 = pque.top();
25             pque.pop();
26             L2 = pque.top();
27             pque.pop();
28 
29             ans += (long long)L1 + L2;
30             pque.push(L1 + L2);
31         };
32         printf("%lld\n", ans);
33     }
34 }

这是用的std，事实上呢用std是挺方便的，虽然稍微损失了一下性能，我直接用堆是472K,32ms，用std是920k,47ms，相差不大

 

另外这个思想还可以用来做著名的Huffman编码，其实Huffman以前写了一个，以后会贴出来看看

 

posted @ 2015-09-06 20:25  PhiliAI  阅读(677)  评论(0)  编辑  收藏  举报