位运算

一、什么是位运算？

位运算(Bit Manipulation,也叫位操作)说穿了，就是直接对整数在内存中的二进制位进行操作。

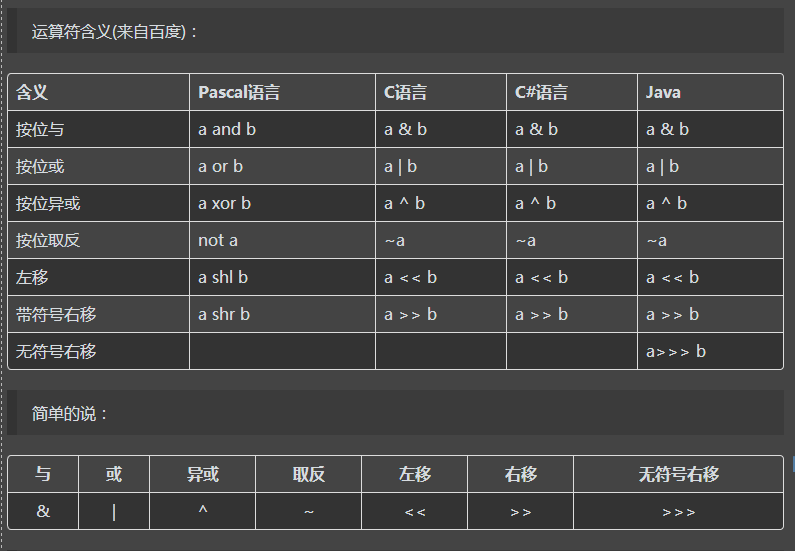
优先级(可以放在最后记忆)

二、优点、缺点。

2.1 优点，同时也可以理解为：1.位运算有什么用; 2.用在什么地方。

1. 提高速度，节省空间(有时也能节省代码量)。
   因为位运算是直接操作二进制，所以避免了进制转换，类型转换提高了计算速度。如5<<3 相当于 52^3=58=40;
   对于这一点速度，对于语言高级层面可能显得并不那么重要，但在低层(大量使用时或循环中)，就很明显了。
   注：嵌入式，硬件，驱动，编码
2. 联合表示多个bool值。
   一个byte可以存储8个逻辑值，在算法竞赛中，状态压缩是最明显的一个应用。
3. 有些地方我们必须要使用位运算来处理，比如权限。
   a&~b: 清除标志位b;
   a|b: 添加标志位b;
   a&b: 取出标志位b;
   a^b: 取出a与b的不同部分;

public class Permission {
    // 是否允许查询
    private boolean allowSelect;
    // 是否允许新增
    private boolean allowInsert;
    // 是否允许删除
    private boolean allowDelete;
    // 是否允许更新
    private boolean allowUpdate;
    // 省略Getter和Setter
}

public class NewPermission {
    // 是否允许查询，二进制第1位，0表示否，1表示是
    public static final int ALLOW_SELECT = 1 << 0; // 0001
    // 是否允许新增，二进制第2位，0表示否，1表示是
    public static final int ALLOW_INSERT = 1 << 1; // 0010
    // 是否允许修改，二进制第3位，0表示否，1表示是
    public static final int ALLOW_UPDATE = 1 << 2; // 0100
    // 是否允许删除，二进制第4位，0表示否，1表示是
    public static final int ALLOW_DELETE = 1 << 3; // 1000
    // 存储目前的权限状态
    private int flag;

    //重新设置权限
    public void setPermission(int permission) {
        flag = permission;
    }
    //添加一项或多项权限
    public void enable(int permission) {
        flag |= permission;
    }
    //删除一项或多项权限
    public void disable(int permission) {
        flag &= ~permission;
    }
    //是否拥某些权限
    public boolean isAllow(int permission) {
        return (flag & permission) == permission;
    }
    //是否禁用了某些权限
    public boolean isNotAllow(int permission) {
        return (flag & permission) == 0;
    }
    //是否仅仅拥有某些权限
    public boolean isOnlyAllow(int permission) {
        return flag == permission;
    }
}

2.2 缺点

缺点其实很明显：

1. 不了解位运算的人可能完全看不懂；
2. 可读性差，即使对位运算相对比较了解的人 一下子也可能感觉不明所以。

三、详解位运算符

3.1 按位与运算(&)， 同为1，则为1.

含义(用法)：按位与运算通常用来对某些位清0或保留某些位。
如：a&255或a&0xff，因为255的二进制为1111 1111，与的结果为a只保留低8位。
再如：a = a&(~7),因为~7为1111 1000(假如1个字节)，与的结果为a的低3位置为0。

注：

• 255，7等数字并非随意，需要根据自己的意图选取，如使a的第2个字符转为0，a&(~0xF0)
• 当初我就迷惑:仅仅将某此位转为0或1有何用？（后来明白跟其它位运算符结合使用都会突显各自的作用）

3.2 按位或运算(|),有1，则为1.

含义(用法):将某些位置为1.
如：8|4 => 1000b|0100b => 1100b =>12,单看没啥用，如果用在权限上(授予权限),啧啧..

3.3 按位异或运算(^)，不同，则为1.

含义(用法):求出两个数的差异。

3.4 求反运算(~),1则为0，0则为1.

3.5 左移<<,右移>>,无符号右移>>>.

1. <<n左移n位,右补0。实际含义相当于*2^n
2. >>n右移n位，左补0.实际含义相当于/2^n
3. >>>n右移n位，正数左补0，负数取决于编译系统，一般补1

四、常用操作

1. 平均值
   (x+y)>>1
2. 2的n次方
   1 << n
3. 判断符号是否相同
   (x^y)>=0
4. 交换两个数
   a ^= b;
   b ^= a;
   a ^= b;
5. 判断奇偶性
   (n &1) ==1
6. 取绝对值
   (n ^ (n >> 31)) - (n >> 31)
7. 判断n是否是2的整数次幂
   n&(n-1) == 0
8. 其它

1.将expr的第n（n从0开始）位设置为1: expr |= (1<<n);
2.将expr的第n（n从0开始）位设置为0: expr &= (~(1<<n));
3.判断expr的第n（n从0开始）位是否为1：bool b =expr & (1<<n);
4.翻转expr的第n（n从0开始）位：expr ^=(1<<n)；

五、链接、参考、QQ群

1. 本文链接，作业部落
2. 简书文集之二进制
3. QQ群之专精位运算,点击即可加群662979096