【Bzoj 1835 基站选址】
基站选址的区间里隐藏着DP优化的机密……
分析:
不论是做过乘积最大还是石子合并,或者是其他的入门级别的区间DP题目的人呐,大米并认为读题后就能够轻松得出一个简洁明了的Dp转移方程。
由于这道题每个村庄i仅有两种状态:①自己有一个基站②自己不是基站,但是自己的范围S[i]里有基站。基于这样的关系,可以得出一个容易理解的Dp转移方程:
[设f[k][i]表示1~i的村庄中选取k个村庄安放基站,并且第k个村庄就安放在村庄i,使得所有村庄合法的最小花费]
f[k][i]=min(f[k-1][j]+Cost(j,i))+c[i] (j<i)
这个状态转移表达的含义是,村庄i,j安放了基站。据此Cost(i,j)表示的则是在村庄i,j之间没能接收到基站信号的基站的额外费用w[i]之和(即表示由于不能用基站处理掉而付出的额外代价)。
到此为止这个解法已经成功了一半。不成功的地方是时间复杂度在本提数据范围下是不能承受的——O(n2k)。
因此我们考虑Dp的优化。让我们幻想一下,如果能够存下f[k-1][]+Cost们的最优值,那么就不需要对于每个i转移花n次来枚举来源了!随后可以发现,难点在于Cost(i,j)的快速计算。
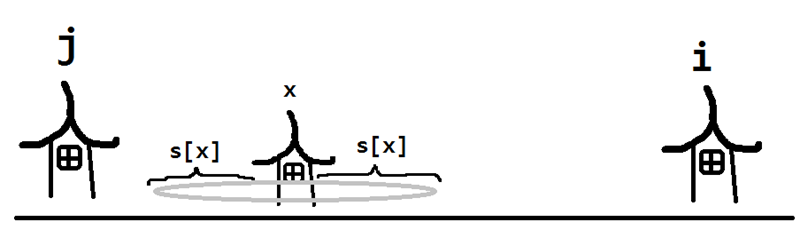
仔细分析Cost(i,j)的定义,我们需要找到一种方法,能够快速求出在两个基站i,j之间有哪些村庄无法被覆盖(调皮的是,这里覆盖范围是按各个村庄来定的)。由于f[k][i]表示合法方案,所以在状态转移的时候,我们要注意对于[1,j]之间的村庄已经处理好,我们只要考虑(j,i)中村庄是否覆盖的问题。那么如果一个村庄无法被j,i两个村庄覆盖,它的信号接收范围长啥样呢?
就是这样:左手摸不着j,右手碰不到i。然后我们尝试利用范围这一特性,我们发现,如果(j,i)这一对组合,x覆盖不到,那么对于所有(j,I)(I大于i)都覆盖不到x。所以我们想到,一种(j,i)可以为后来的(j,I)提供一些小小信息。同理地,如果(j,i)这一对组合,x覆盖不到,那么对于所有(J,i)(J小于j)都覆盖不到x。总结来说啦,就是一种单调性:
结论:如果状态转移中(j,i)情况下(表示在i,j放置基站),如果之间某个村庄x无法被覆盖,那么对于所有状态转移中(J,I)[J<j&&I>i]都无法覆盖x(毕竟越来越远了嘛)。
为了方便,我们动用三个数组参与Dp的优化行动:
·int left_cur[i]:表示在村庄i的范围内[-s[i],+s[i]],最靠左边的那个村庄的位置(也就是下标最小的点,放置基站依旧可以覆盖i);
·int left_cur[i]:表示在村庄i的范围内[-s[i],+s[i]],最靠右边的那个村庄的位置(也就是下标最大的点,放置基站依旧可以覆盖i);
·vector<int> cur_right[i]:用于存储所有right_cur的值都为i村庄的点的下标(和前一个玩意儿互逆似的)。
当前状态转移f[k][i]=min(f[k-1][j]+Cost(i,j))+c[i]完成后,我们将以i为 right_cur的值的点全部枚举一遍(使用数组cur_right),对于每个枚举的点再依靠left_cur[i]找到最左边能够覆盖该点的村庄下标p。这样做是干啥呢?因为i即将循环至i+1那么下面的状态对于所有(P,I)[P<p,I>i]都不可能覆盖这些枚举的点了,那么这些点的w(额外费用)必然会贡献Cost所以我们先给这些点(即1~p-1的点)加上这个Cost,然后维护这些f[k-1][]+Cost的最小值用于下一次转移就可以了——用啥维护可以支持区间加和区间求最值?线段树!
代码长出来了:
1 #include<vector> 2 #include<stdio.h> 3 #include<algorithm> 4 #define ll long long 5 #define inf 1ll*100000000*100000000 6 #define In(a,p) go(i,p,n)scanf("%d",a+i) 7 #define go(i,a,b) for(int i=a;i<=b;i++) 8 #define ro(i,a,b) for(int i=a;i>=b;i--) 9 using namespace std; 10 const int N=20003;int n,K; 11 ll d[N],c[N],s[N],w[N],f[N],left_cur[N],ans=inf,W; 12 vector<int>cur_right[N]; 13 struct Binary_Search 14 { 15 int l,r,M,res; 16 int Left_Search(int i){l=1,r=res=i; 17 while(l<=r)d[i]-d[M=l+r>>1]<=s[i]?res=M,r=M-1:l=M+1;return res;} 18 int Right_Search(int i){l=res=i,r=n; 19 while(l<=r)d[M=l+r>>1]-d[i]<=s[i]?res=M,l=M+1:r=M-1;return res;} 20 }dichotomy; 21 struct Segment_Tree 22 { 23 int sz,lch[N*4],rch[N*4];ll lazy[N*4],Min[N*4]; 24 void Init(){sz=0;int _;Build(_,1,n);} 25 void Push_Up(int u){Min[u]=min(Min[lch[u]],Min[rch[u]]);} 26 void Push_Down(int u) 27 { 28 lazy[lch[u]]+=lazy[u];lazy[rch[u]]+=lazy[u]; 29 Min[lch[u]]+=lazy[u];Min[rch[u]]+=lazy[u];lazy[u]=0; 30 } 31 void Build(int &u,int l,int r) 32 { 33 lazy[u=++sz]=0;if(l==r){Min[u]=f[l];return;} 34 int M=l+r>>1;Build(lch[u],l,M);Build(rch[u],M+1,r);Push_Up(u); 35 } 36 void Update(int u,int l,int r,int L,int R,ll d) 37 { 38 if(L>R)return;Push_Down(u); 39 if(l==L&&r==R){Min[u]+=d;lazy[u]+=d;return;} 40 int M=l+r>>1;if(R<=M)Update(lch[u],l,M,L,R,d); 41 else if(L>M)Update(rch[u],M+1,r,L,R,d); 42 else Update(lch[u],l,M,L,M,d),Update(rch[u],M+1,r,M+1,R,d);Push_Up(u); 43 } 44 ll Query(int u,int l,int r,int L,int R) 45 { 46 if(L>R)return 0;Push_Down(u); 47 if(l==L&&r==R){return Min[u];} 48 int M=l+r>>1;if(R<=M)return Query(lch[u],l,M,L,R); 49 else if(L>M)return Query(rch[u],M+1,r,L,R); 50 else return min(Query(lch[u],l,M,L,M),Query(rch[u],M+1,r,M+1,R));Push_Up(u); 51 } 52 }maintain; 53 int main() 54 { 55 scanf("%d%d",&n,&K);In(d,2);In(c,1);In(s,1);In(w,1); 56 57 go(i,1,n) 58 { 59 left_cur[i]=dichotomy.Left_Search(i); 60 int right=dichotomy.Right_Search(i); 61 cur_right[right].push_back(i); 62 } 63 n++;K++;w[n]=d[n]=inf; 64 65 go(i,1,n){f[i]=c[i];go(j,1,i-1)if(d[j]+s[j]<d[i])f[i]+=w[j];}ans=f[n]; 66 go(k,2,K) 67 { 68 maintain.Init();go(i,1,n) 69 { 70 f[i]=maintain.Query(1,1,n,1,i-1)+c[i]; 71 if(cur_right[i].size())go(j,0,cur_right[i].size()-1) 72 { 73 int Pos=cur_right[i][j]; 74 maintain.Update(1,1,n,1,left_cur[Pos]-1,w[Pos]); 75 } 76 } 77 ans=min(ans,f[n]); 78 } 79 printf("%lld\n",ans);return 0; 80 }//Paul_Guderian
有人说大米饼喜欢压代码,这里有一份不压的————我也会写不压的!

1 #include<vector> 2 #include<stdio.h> 3 #include<algorithm> 4 #define ll long long 5 #define inf 1ll*100000000*100000000 6 #define In(a,p) go(i,p,n)scanf("%d",a+i) 7 #define go(i,a,b) for(int i=a;i<=b;i++) 8 #define ro(i,a,b) for(int i=a;i>=b;i--) 9 using namespace std; 10 const int N=20003;int n,K; 11 ll d[N],c[N],s[N],w[N],f[N],left_cur[N],ans=inf,W; 12 vector<int>cur_right[N]; 13 struct Binary_Search 14 { 15 int l,r,mid; 16 int Left_Search(int i) 17 { 18 l=1,r=i;int res=i; 19 while(l<=r) 20 { 21 mid=l+r>>1; 22 if(d[i]-d[mid]<=s[i])res=mid,r=mid-1; 23 else l=mid+1; 24 } 25 return res; 26 } 27 int Right_Search(int i) 28 { 29 l=i,r=n;int res=i; 30 while(l<=r) 31 { 32 mid=l+r>>1; 33 if(d[mid]-d[i]<=s[i])res=mid,l=mid+1; 34 else r=mid-1; 35 } 36 return res; 37 } 38 }dichotomy; 39 struct Segment_Tree 40 { 41 int sz,lch[N*4],rch[N*4];ll lazy[N*4],Min[N*4]; 42 void Init(){sz=0;int _;Build(_,1,n);} 43 void Push_Up(int u) 44 { 45 Min[u]=min(Min[lch[u]],Min[rch[u]]); 46 } 47 void Push_Down(int u) 48 { 49 lazy[lch[u]]+=lazy[u]; 50 lazy[rch[u]]+=lazy[u]; 51 Min[lch[u]]+=lazy[u]; 52 Min[rch[u]]+=lazy[u]; 53 lazy[u]=0; 54 } 55 void Build(int &u,int l,int r) 56 { 57 lazy[u=++sz]=0; 58 if(l==r) 59 { 60 Min[u]=f[l]; 61 return; 62 } 63 int M=l+r>>1; 64 Build(lch[u],l,M); 65 Build(rch[u],M+1,r); 66 Push_Up(u); 67 } 68 void Update(int u,int l,int r,int L,int R,ll d) 69 { 70 if(L>R)return; 71 Push_Down(u); 72 if(l==L&&r==R) 73 { 74 Min[u]+=d; 75 lazy[u]+=d; 76 return; 77 } 78 int M=l+r>>1; 79 if(R<=M)Update(lch[u],l,M,L,R,d); 80 else if(L>M)Update(rch[u],M+1,r,L,R,d); 81 else Update(lch[u],l,M,L,M,d),Update(rch[u],M+1,r,M+1,R,d); 82 Push_Up(u); 83 } 84 ll Query(int u,int l,int r,int L,int R) 85 { 86 if(L>R)return 0; 87 Push_Down(u); 88 if(l==L&&r==R) 89 { 90 return Min[u]; 91 } 92 int M=l+r>>1; 93 if(R<=M)return Query(lch[u],l,M,L,R); 94 else if(L>M)return Query(rch[u],M+1,r,L,R); 95 else return min(Query(lch[u],l,M,L,M),Query(rch[u],M+1,r,M+1,R)); 96 Push_Up(u); 97 } 98 }maintain; 99 void Input_Data() 100 { 101 scanf("%d%d",&n,&K); 102 In(d,2);In(c,1);In(s,1);In(w,1); 103 } 104 void Add_Ans_Point() 105 { 106 n++;K++; 107 w[n]=d[n]=inf; 108 } 109 void Pre_Handle_of_Dynamic_Programming() 110 { 111 go(i,1,n) 112 { 113 left_cur[i]=dichotomy.Left_Search(i); 114 int right=dichotomy.Right_Search(i); 115 cur_right[right].push_back(i); 116 } 117 Add_Ans_Point(); 118 } 119 void Init_First_Status() 120 { 121 go(i,1,n) 122 { 123 f[i]=c[i]; 124 go(j,1,i-1) 125 { 126 if(d[j]+s[j]<d[i]) 127 { 128 f[i]+=w[j]; 129 } 130 } 131 } 132 } 133 void Optimized_Dynamic_Programming() 134 { 135 Init_First_Status(); 136 ans=f[n]; 137 go(k,2,K) 138 { 139 maintain.Init(); 140 go(i,1,n) 141 { 142 f[i]=maintain.Query(1,1,n,1,i-1)+c[i]; 143 if(cur_right[i].size()) 144 { 145 go(j,0,cur_right[i].size()-1) 146 { 147 int Pos=cur_right[i][j]; 148 maintain.Update(1,1,n,1,left_cur[Pos]-1,w[Pos]); 149 } 150 } 151 } 152 ans=min(ans,f[n]); 153 } 154 printf("%lld\n",ans); 155 } 156 int main() 157 { 158 freopen("in.in","r",stdin); 159 160 Input_Data(); 161 162 Pre_Handle_of_Dynamic_Programming(); 163 164 Optimized_Dynamic_Programming(); 165 166 return 0; 167 }//Paul_Guderian
我无法忘记那只廉价的吉他
和那件破旧的蓝色军装。————汪峰《雨天的回忆》