【NOIP2012-开车旅行】

这道题：你不仅要学会两人交换开车，还要做到高效驾驶。

 

·分析：

      在拨开花哨题目的迷雾之后，发现两个重要突破口：

      ①从每个点开始，他们的路径是一定的，不存在决策选取。

      ②要是n,m没有那么大的话，就直接预处理每个点对于每个人开车至下一个点的位置和路程(n2)，然后两个问题都可以从起点（第一问就是枚举起点）开始预处理的数据来“轮流开车”。（这一个突破口有点过于顶尖了，因为这是过70%数据的题解）

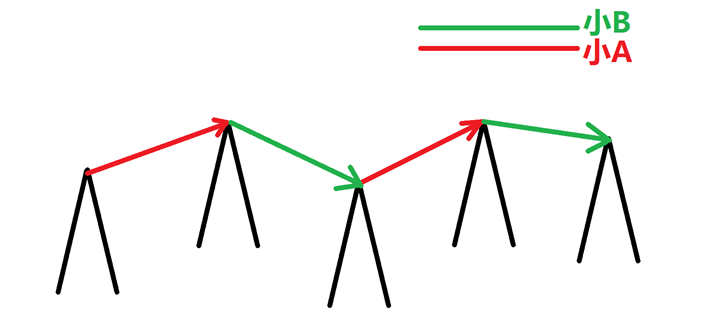
      下图是这种做法的简图。

      用des[i][0],des[i][1]分别表示在城市i小B开车和小A开车前往的下一个目的地。用Min[i][0],Min[i][1]分别与上面的数组对应，表示对应路径的长度（注意是反向枚举）

          image

·无论是第一问还是第二问，都可以从起点s开始，通过des,Min数组来向后开车并记录两人各自走的路程。

·很美妙但又很遗憾，仅仅这样做时间复杂度：(n2+nm)

·这道题真正的考点就出来了：考察我们的优化技能。

·很轻易可以发现，这道题的数据范围又给了我们很大的提示：

n<=100000。这启示我们：nlogn

·余下的事情就是把时间复杂度中的部分n替换成logn,使得时间复杂度保持在：O(mlogn+nlogn)【这有点过于顶尖了】

·在本题中大米饼的对策是：预处理des,Min(这原来是一个n2)时使用STL中的set来维护(降为nlogn),在路径上使用倍增法，

·最后一个值得注意的一点，倍增的每一段为了方便操作，这里AB各走一次算成一段，不过倍增的距离还是对AB进项单独维护。整个程序还有许多细节需要注意。 wow!

 

 1 #include<stdio.h> 
 2 #include<algorithm>
 3 #include<set>
 4 #define go(i,a,b) for(int i=a;i<=b;i++)
 5 #define ro(i,a,b) for(int i=a;i>=b;i--)
 6 #define inf 2147483645
 7 #define eps 0.000003
 8 using namespace std;const int N=100005;
 9 int n,m,s,h[N],des[N][2],Min[N][2],To[N][22],dis[N][22][2],tot[2],x;
10 struct info{int h,id;bool operator<(const info a)const{return h<a.h;};};
11 set<info>box;set<info>::iterator I;int A(int t){return t<0?-t:t;}
12 void consider(int i,info p)
13 {
14     int j=p.id;
15     if((A(h[i]-h[j])<Min[i][0])||(Min[i][0]==A(h[i]-h[j])&&h[j]<h[des[i][0]]))
16     {
17         if((Min[i][0]<Min[i][1])||(Min[i][1]==Min[i][0]&&h[des[i][0]]<h[des[i][1]]))
18         Min[i][1]=Min[i][0],des[i][1]=des[i][0];
19         Min[i][0]=A(h[i]-h[j]),des[i][0]=j;    
20     }
21     else if((A(h[i]-h[j])<Min[i][1])||(Min[i][1]==A(h[i]-h[j])&&h[j]<h[des[i][0]]))
22     Min[i][1]=A(h[i]-h[j]),des[i][1]=j;    
23 }
24 void doubling(int i,int val)
25 {
26     ro(k,20,0)if(dis[i][k][0]+dis[i][k][1]<=val&&To[i][k])
27         val-=(dis[i][k][0]+dis[i][k][1]),
28         tot[1]+=dis[i][k][1],tot[0]+=dis[i][k][0],i=To[i][k];    
29     if(des[i][1]&&Min[i][1]<=val)tot[1]+=Min[i][1];
30 }
31 int main(){scanf("%d",&n);go(i,1,n)scanf("%d",&h[i]),Min[i][1]=Min[i][0]=inf;
32     ro(i,n,1)
33     {    
34         box.insert((info){h[i],i});
35         I=box.find((info){h[i],i});++I;
36         if(I!=box.end())consider(i,*I),++I,I!=box.end()?consider(i,*I),1:1,--I;--I;
37         if(I!=box.begin())--I,consider(i,*I),I!=box.begin()?--I,consider(i,*I),1:1;
38     }
39     
40     go(i,1,n)To[i][0]=des[des[i][1]][0],
41     dis[i][0][1]=Min[i][1],dis[i][0][0]=Min[des[i][1]][0];
42             
43     go(k,1,20)go(i,1,n)To[i][k]=To[To[i][k-1]][k-1],
44     dis[i][k][1]=dis[i][k-1][1]+dis[To[i][k-1]][k-1][1],
45     dis[i][k][0]=dis[i][k-1][0]+dis[To[i][k-1]][k-1][0];
46         
47     scanf("%d",&x);double rate=inf;int pos=0;h[0]=-inf;go(i,1,n)
48     {
49         tot[0]=tot[1]=0;doubling(i,x);double tmp=tot[0]?1.0*tot[1]/tot[0]:inf;
50         if(tmp-rate<eps&&tmp-rate>-eps&&h[i]>h[pos])pos=i;
51         if(rate-tmp>eps)pos=i,rate=tmp;
52     }
53     
54     printf("%d\n",pos);scanf("%d",&m);go(i,1,m)
55     {
56         scanf("%d%d",&s,&x);
57         tot[0]=tot[1]=0;doubling(s,x);
58         printf("%d %d\n",tot[1],tot[0]);
59     }
60     return 0;
61 }//Paul_Guderian

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

只许集中，不许分散。————海因茨·威廉·古德里安

 

posted @ 2017-05-14 17:43  大米饼  阅读(320)  评论(0)  编辑  收藏  举报