LCS小结(O(∩_∩)O~吽吽)
LCS!~如果你在百度上搜这个的话会出来”英雄联盟冠军联赛”,orz。。但是今天要讲的LCS是最长公共子序列 ,"Longest Common Subsequence "not"League of Legends Championship Series "小盆友们又要涨姿势了~
最长公共子序列也称作最长公共子串(不要求连续),打个比方说,A君有一个字符串:qazwbx,B君也有一个字符串:azwsxq,那么我们可以说a君和B君的最长公共子序列为:azwx,长度为4,这样看来好像挺简单的,但是如果字符串很长或者比较的字符串个数很多,要求出公共的而且是最长的就能比较困难了,为了方便小盆友们方便的求得 最长公共子序列,我们引入高大上的DP君!
这里我们采用的是矩阵实现,也就是二维数组。
第一步:先计算最长公共子序列的长度。
第二步:根据长度,然后通过回溯求出最长公共子序列。
先来实现第一步吧:
设一个C[i][j]: 保存Xi与Yj的LCS的长度。
设X = { x1~xm },Y = { y1~yn }及它们的最长子序列Z = { z1~zk }则:
1、若 xm = yn , 则 zk = xm = yn,且Z[k-1] 是 X[m-1] 和 Y[n-1] 的最长公共子序列
2、若 xm != yn ,且 zk != xm , 则 Z 是 X[m-1] 和 Y 的最长公共子序列
3、若 xm != yn , 且 zk != yn , 则 Z 是 Y[n-1] 和 X 的最长公共子序列
子问题的递归结构:
当 i = 0 , j = 0 时 , c[i][j] = 0
当 i , j > 0 ; xi = yi 时 , c[i][j] = c[i-1][j-1] + 1
当 i , j > 0 ; xi != yi 时 , c[i][j] = max { c[i][j-1] , c[i-1][j] }
下面的代码是求两个字符串的最长公共子串:
1 int LCS(int n,int m)//n,m分别为两个字符串的长度 2 { 3 int i,j; 4 int len=max(n,m); 5 for(i=0;i<=len;i++) 6 { 7 dp[i][0]=0; 8 dp[0][i]=0; 9 } 10 for(i=1;i<=n;i++) 11 { 12 for(j=1;j<=m;j++) 13 { 14 if(a[i-1]==b[j-1]) 15 { 16 dp[i][j]=dp[i-1][j-1]+1; 17 } 18 else 19 { 20 dp[i][j]=max(dp[i-1][j],dp[i][j-1]); 21 } 22 } 23 } 24 return dp[n][m]; 25 }
第二步:通过回溯求出最长公共子序列
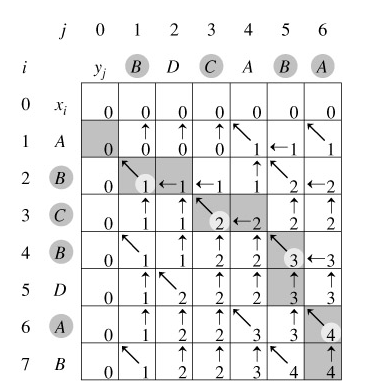
如图:
下面给出逆序输出最长公共子串的代码:
1 int i=n-1,j=m-1,count=k; 2 while(count!=0) 3 { 4 if(a[i]==b[j]) 5 { 6 cout<<a[i]; 7 i--; 8 j--; 9 count--; 10 } 11 else if(dp[i][j-1]>dp[i-1][j]) 12 { 13 j--; 14 } 15 else 16 { 17 i--; 18 } 19 }cout<<endl;
从最后开始,碰到一样的输出,不一样的,往更大的方向跑。其实就是前面生成dp的逆过程。
LCS粗略的讲完了,还有很多不足,希望大家多多补充~



