浅谈图的深度优先遍历

一、图的深度优先概述

图，就是由一些小圆点（称为顶点）和连接这些小圆点的直线（称为边）组成的。例如：

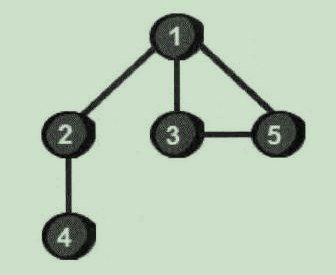
上图是由五个顶点（编号为1、2、3、4、5）和五条边（1-2、1-3、1-5、2-4、3-5）组成。

 

现在我们从1号顶点开始遍历这个图（遍历指的是把每一个顶点都访问一次）。使用深度优先搜索来遍历这个图我们将得到以下结果：

 

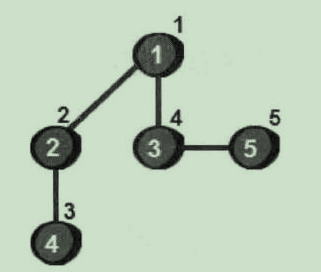
使用深度优先搜索来遍历这个图的具体过程是：

1. 首先从一个未走到过的顶点作为起始顶点，比如1号顶点作为起点。
2. 沿1号顶点的边去尝试访问其它未走到过的顶点，首先发现2号顶点还没有走到过，于是来到了2号顶点。
3. 再以2号顶点作为出发点继续尝试访问其它未走到过的顶点，这样又来到了4号顶点。
4. 再以4号顶点作为出发点继续尝试访问其它未走到过的顶点。
5. 但是，此时沿4号顶点的边，已经不能访问到其它未走到过的顶点了，所以需要返回到2号顶点。
6. 返回到2号顶点后，发现沿2号顶点的边也不能再访问到其它未走到过的顶点。此时又会来到3号顶点（2->1->3），再以3号顶点作为出发点继续访问其它未走到过的顶点，于是又来到了5号顶点。
7. 至此，所有顶点我们都走到过了，遍历结束。

深度优先遍历的主要思想是：

1. 首先以一个未被访问过的顶点作为起始顶点，沿当前顶点的边走到未访问过的顶点；
2. 当没有未访问过的顶点时，则回到上一个顶点，继续试探别的顶点，直到所有的顶点都被访问过。

在此我想用一句话来形容 “一路走到头，不撞墙不回头”。

 

二、实现

显而易见，深度优先搜索遍历是沿着图的某一条分支遍历直到末端，然后回溯，再沿着另一条进行同样的遍历，直到所有的顶点都被访问过为止。

那么问题来了，该如何实现这一过程呢？

首先，我们来解决如何存储一个图的问题。最常用的方法是使用一个二维数组e来存储，如下：

 

上图二维数组中第 i 行第 j 列表示的就是顶点 i 到顶点 j 是否有边。1 表示有边，∞ 表示没有边，0 表示自己到自己（i=j）。这种存储图的方法称为图的邻接矩阵存储法。

同时我们发现：这个二维数组是沿着主对角线对称的，因此上面这个图是无向图。无向图指的是图的边没有方向，例如边1-5表示，1号顶点可以到5号顶点，5号顶点也可以到达1号顶点。

void dfs(int cur)//cur是当前所在的顶点编号 
{
    printf("%d ",cur);
    sum++;  //每访问一个顶点sum就加1 
    if(sum==n) return;  //所有的顶点都已经访问过则直接退出 
    for(i=1;i<=n;i++)  //从1号顶点到n号顶点依次尝试，看哪些顶点与当前顶点cur有边相连 
    {
        //判断当前顶点cur到顶点i是否有边，并判断顶点i是否已访问过
        if(e[cur][i]==1 && book[i]==0)
        {
            book[i]==1;  //标记顶点i已经访问过 
            dfs(i);  //从顶点i再出发继续遍历 
         } 
    }
    return;
 } 

 

在上面的代码中变量cur存储的是当前正在遍历的顶点，二维数组e存储的就是图的边（邻接矩阵），数组 book 用来记录哪些顶点已经访问过，变量 sum 用来记录已经访问过多少个顶点，变量 n 存储的是图的顶点的总个数。完整代码如下：

#include<stdio.h>
int book[101],sum,n,e[101][101];
void dfs(int cur)//cur是当前所在的顶点编号 
{
    int i;
    printf("%d ",cur);
    sum++;  //每访问一个顶点sum就加1 
    if(sum==n) return;  //所有的顶点都已经访问过则直接退出 
    for(i=1;i<=n;i++)  //从1号顶点到n号顶点依次尝试，看哪些顶点与当前顶点cur有边相连 
    {
        //判断当前顶点cur到顶点i是否有边，并判断顶点i是否已访问过
        if(e[cur][i]==1 && book[i]==0)
        {
            book[i]==1;  //标记顶点i已经访问过 
            dfs(i);  //从顶点i再出发继续遍历 
         } 
    }
    return;
 } 
 
 int main()
 {
     int i,j,m,a,b;
     scanf("%d %d",&n,&m);
     for(i=1;i<=n;i++)  //初始化二维矩阵
         for(j=1;j<=n;j++)
             if(i == j) e[i][j]=0;
             else e[i][j]=99999999;  //在这里假设99999999为正无穷 
             
    //读入顶点之间的边         
    for(i=1;i<=m;i++)
    {
        scanf("%d %d",&a,&b);
        e[a][b] = 1;  
        e[b][a] = 1;//这里是无向图，所以需要将e[b][a]也赋为1 
     } 
     
    //从1号顶点出发
    book[1]=1;  //标记1号顶点已被访问 
    dfs(1);  //从1号顶点开始遍历 
    
    getchar();getchar();
    return 0; 
 }