算法导论 第三部分——基本数据结构——红黑树
红黑树
红黑树是一种二叉查找树,但在每个结点上增加了一个存储位表示结点的颜色,可以是RED或者BLACK。通过对任何一条从根到叶子的路径上各个着色方式的限制,
红黑树确保没有一条路径会比其他路径长出两倍,因而是接近平衡的。当二叉查找树的高度较低时,这些操作执行的比较快,但是当树的高度较高时,这些操作的性能可能
不比用链表好。红黑树(red-black tree)是一种平衡的二叉查找树,它能保证在最坏情况下,基本的动态操作集合运行时间为O(lgn)。
1、红黑树的性质
#define RED 0 #define BLACK 1 struct RedBlackTreeNode { T key; struct RedBlackTreeNode * parent; struct RedBlackTreeNode * left; struct RedBlackTreeNode * right; int color; };
红黑树的性质如下:
(1)每个结点或是红色,或是黑色。
(2)根结点是黑色。
(3)每个叶子结点(NIL)是黑色。
(4)如果有一个结点是红色,则它的两个儿子都是黑色。
(5)对每个结点,从该结点到其孙子结点的所有路径上包含相同数目的黑色结点。
黑高:从某一结点x出发(不含该结点)到达一个叶节点的任意一条简单路径上的黑色结点的个数称为该结点的黑高。
记为: bh(x) , 哨兵不计入黑高
如下图是一棵红黑树:
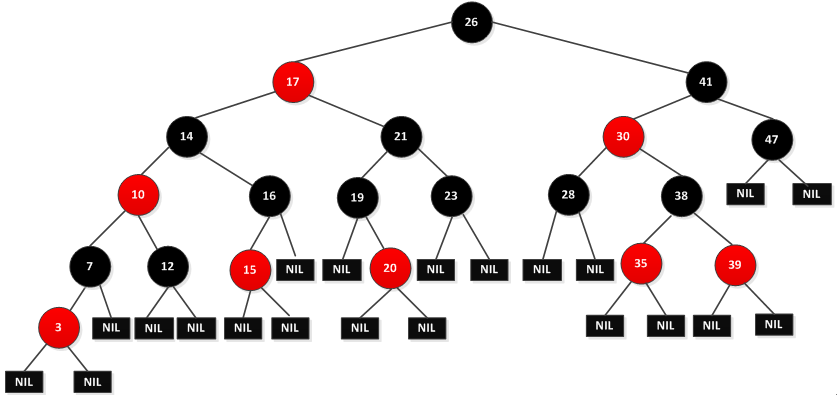
从图可以看出NIL不是空指针,而是一个叶子结点。根结点的父节点也是NIL,实际操作的时候可以将NIL视为哨兵,这样便于对黑红色进行操作。红黑树的操作主要是对内部结点操作,
因为内部结点存储了关键字的值。书中为了便于讨论,忽略了叶子结点的,如是上图红黑树变成如下图所示:
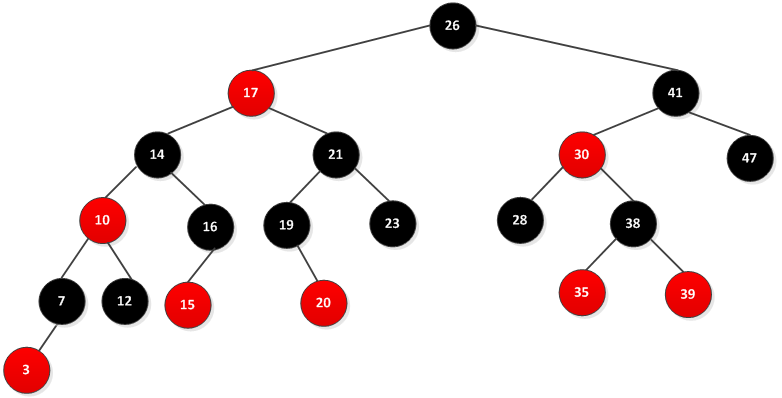
书中给出了黑高度的概念:从某个结点x出发(不包含该结点)到达一个叶子结点的任意一条路径上,黑色结点的个数称为该结点的黑高度。由红黑树的性质(5)可知,
从该结点出发的所有下降路径都有相同的黑色结点个数。红黑树的黑高度定义为其根结点的黑高度。
书中给出了一个引理来说明为什么红黑树是一种好的查找树,并对引理进行了证明(采用归纳法进行证明的,需要很强的归纳推理知识,正是我的不足之处,看书的痛苦在于此)。
引理:一棵有n个内结点的红黑树的高度之多为2lg(n+1)。
// 任意以x为根结点的子树种至少包含2^bh(x)-1个内部结点。
根的黑高至少为h/2 ,所以 n>= 2^(h/2)-1
2、旋转
对于红黑树,search/min/max 与普通二叉搜索树相同。但是delete和insert需要保证操作之后保证红黑树的性质,所以需要在这里介绍旋转。
在红黑树上进行结点插入和删除操作时,会改变树的结构形状,导致结果可能不满足了红黑树的某些性质,为了保证每次插入和删除操作后,仍然能报维持红黑树的性质,需要改变树
中某些结点的颜色和指针结构。其中的指针结构的改变通过旋转完成的。书中给出了两种旋转:左旋转和右旋转。如下图是旋转过程:
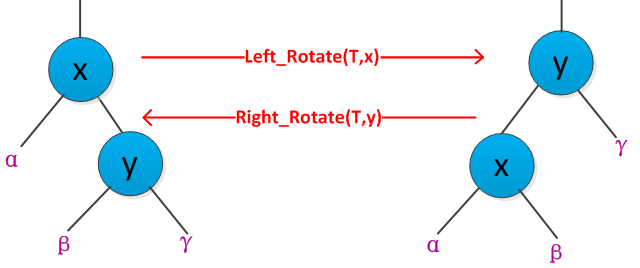
从图可以得出左右旋转的过程,假设对某个结点x进行左旋转,y是x的右孩子,则左旋转过程为:以x和y之间的链为“支轴”进行的,使得x的右孩子为y的左孩子,y的父节点为x的父节点,y的左孩子为x。书中给出了左旋转的伪代码如下:
LEFT_ROTATE(T,x)
y = right[x] //获取右孩子
rihgt[x] = left[y] //设置x的右孩子为y的左孩子
if left[y] != NIL
then parent[left[x]] = x
parent[y] = parent[x] //设置y的父节点为x的父节点
if parent[x] == NIL
then root[T] = y
else if x==left[parent[x]
then left[parent[x]] = y
else right[[parent[x]] = y
left[y] = x //设置y的左孩子为x
parent[x] =y
假设对某个结点y进行右旋转,x是y的左孩子,则左旋转过程为:y的左孩子设置为x的右孩子,将x的父节点设置为y的父节点,x的右孩子设置为y。书中并没有给出右旋转的伪代码,参照左旋转的伪代码很容易实现:
RIGHT_ROTATE(T,y)
x = left[y] //获取左孩子
left[y] = right[x] //设置y的左孩子为x的右孩子
if right[x] != NIL
then parent[right[x]] = y
parent[x] = parent[y] //设为x的父节点为y的父结点
if parent[y] == NIL
then root = x
else if y== left[parent[y]]
then left[parent[y]] = x
else right[parent[y]] = x
right[x] = y //设置x的右孩子为y
parent[y] = x
为了更好的理解旋转操作,书中给出了一个左旋转的例如,如下图所示:
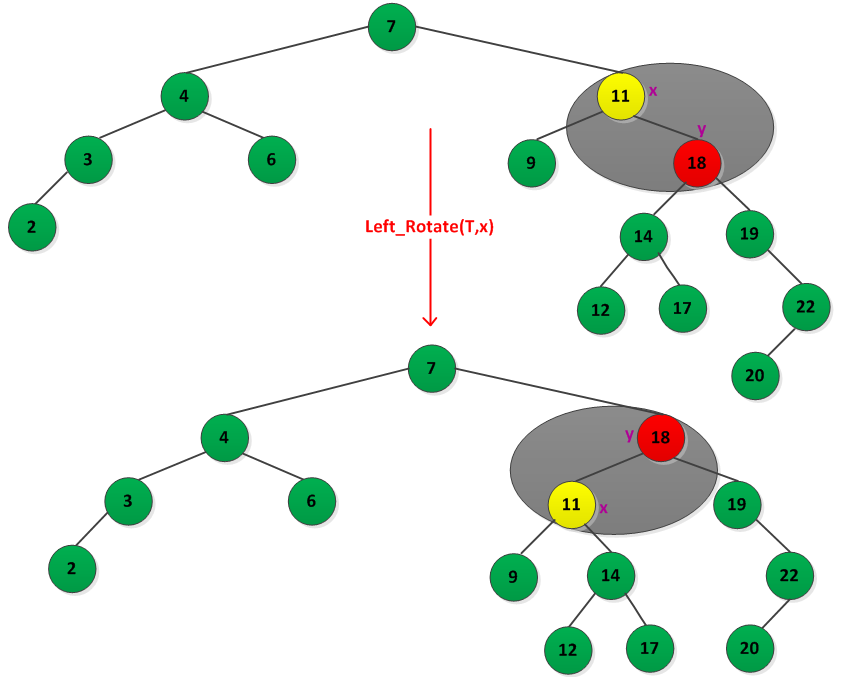
2、红黑树的插入算法
红黑树的插入算法是在搜溹二叉树的基础之上加以改进的,因为插入之后满足搜溹二叉树的性质但是有可能不满足红黑树的部分性质,所以之后需要调用RB-INSERT-FIXUP
修正成红黑树。它的伪代码如下:(参考搜索二叉树的插入:http://www.cnblogs.com/NeilZhang/p/5654393.html)
RB_INSERT(T,z) y = NIL x =root(T) while x != NIL do y=x if key[z]<key[x] then x=left[x] else x=right[x] parent[z] = y if y =NIL then root =z else if key[z] < key[y] then left[y] =z else right[y] =z left[z] = NIL right[z] =NIL color[z] = RED //新插入结点标记为红色 RB_INSERT_FIXUP(T,z) //进行调整,使得满足红黑树性质
红黑树的插入过程最主要的是RB_INSERT_FIXUP过程,书中发了很大的篇幅进行介绍。首先分析了当插入一个新的结点后,会破坏红黑树的哪些性质,然后针对可能的破坏性质进行分类讨论并给出了给出了解决办法。因为每次插入的新元素标记为RED,这样可能性质2(根节点为黑色)和性质4(一个红结点的左右孩子都是黑色的)被破坏。例如下图插入一个新结点,破坏了性质4。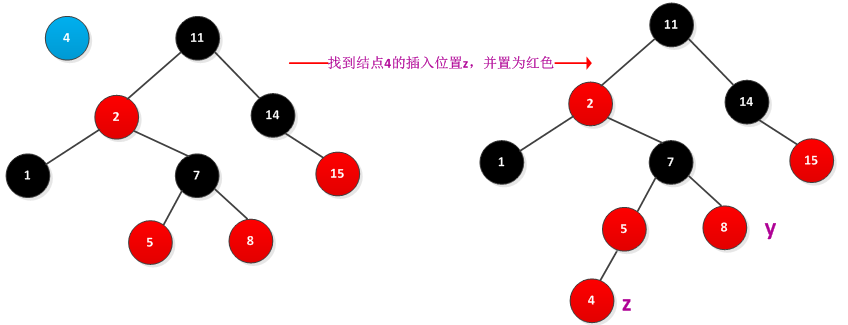
如果每次插入新的结点z导致红黑树性质被破坏,则之多只有一个性质被破坏,并且不是性质2就是性质4。违反性质2是因为z是根且为红色,违反性质4是因为z和其父节点parent[z]都是红色的。
如果性质2被违反了,则红色的根必定是新增的结点z,它是树中唯一的内结点,由于z的父接点和两个子女都是NIL(黑色),不违反性质4。违反性质2在整个插入过程中只有这一次。所以对于
违反性质2的结点,直接将其结点变成黑色即可。
剩下的问题是对于违反性质4的处理,在插入新结点z之前,红黑树的性质没有被破坏。插入结点z后违反性质4,必定是因为z和其父亲结点parent[z]都是红色的,此时只违反性质4,而没有违反
其他性质。假设新插入结点z,导致红黑树性质4被破坏,此时z和其父节点parent[z]都是红色,由于在插入结点z之前红黑树的性质没有被破坏,parent[z]是红色,很容易推出z的祖父结点parent[parent[z]]
必定是黑色。此时根据parent[z]是parent[parent[z]]的左孩子还是右孩子进行讨论。因为左右之间是对称的,书中只给出了parent[z]作为parent[parent[z]]的左孩子进行讨论的,然后给出了三种可能的情况。
情况1):z的叔叔结点y是红色的
此时parent[z]和y都是红色的,解决办法是将z的父节点parent[z]和叔叔结点y都着为黑色,而将z的祖父结点parent[parent[z]]着为红色,然后从祖父结点parent[parent[z]]继续向上判断是否破坏红黑树的性质。处理过程如下图所示: 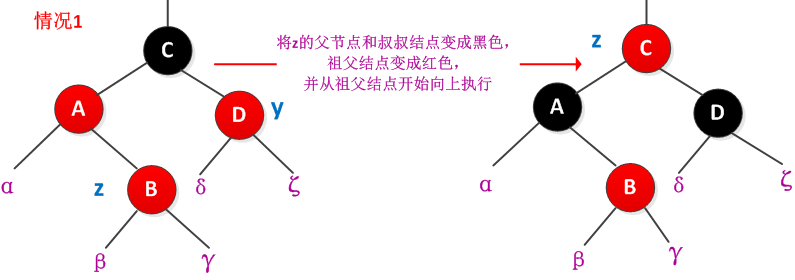
情况2):z的叔叔y是黑色的,而且z是右孩子
情况3):z的叔叔y是黑色的,而且z是左孩子
情况2和情况3中y都是黑色的,通过z是左孩子还是右孩子进行区分的。可以将情况2通过旋转为情况3。情况2中z是右孩子,旋转后成为情况3,使得z变为左孩子,可以在parent[z]结点出使用一次左旋转来完成。无论是间接还是直接的通过情况2进入到情况3,z的叔叔y总是黑色的。在情况3中,将parent[z]着为黑色,parent[parent[z]]着为红色,然后从parent[parent[z]]处进行一次右旋转。情况2、3修正了对性质4的违反,修正过程不会导致其他的红黑性质被破坏。修正过程如下图所示:
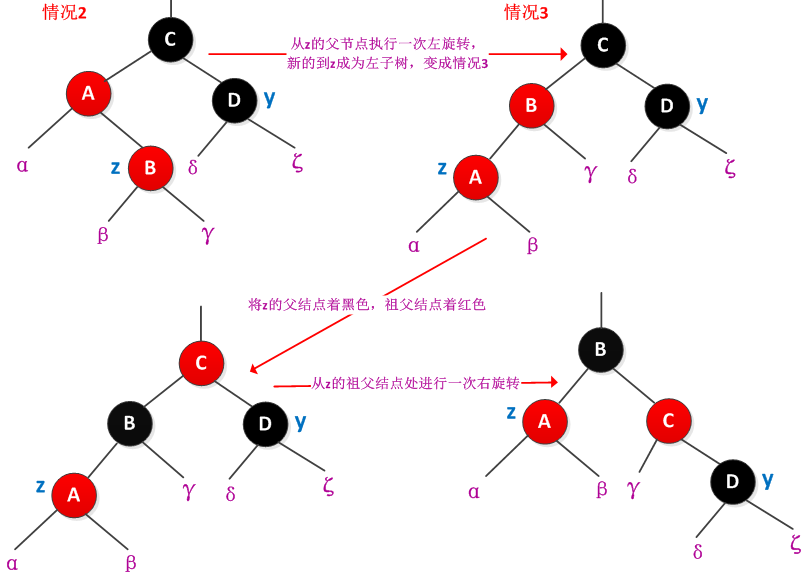
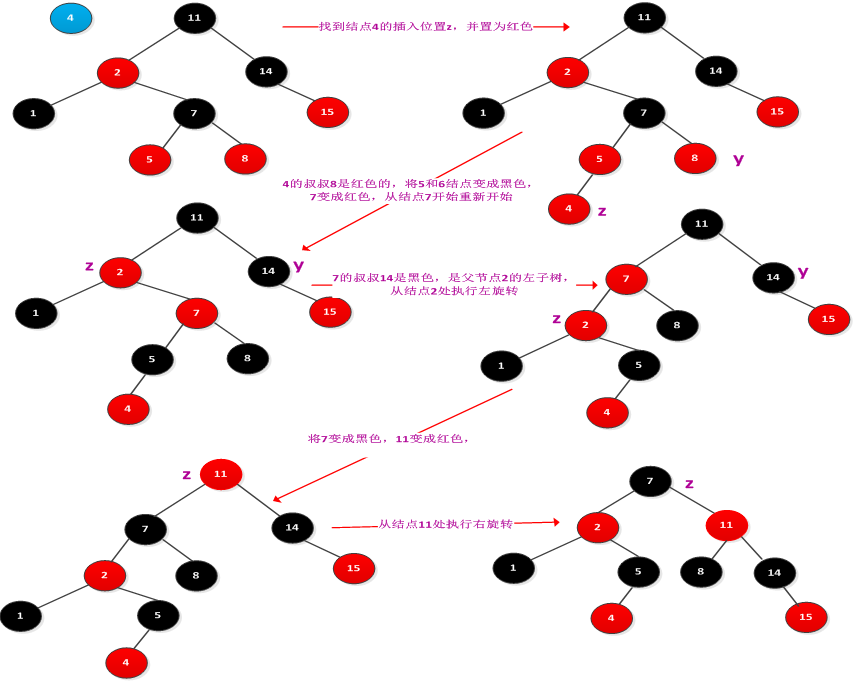
给一个完整的例子来说明插入过程,如下图所示
:
书中给出了RB_INSERT_FIXUP的伪代码,伪代码中只给出了z的父节点为左孩子的情况,为右孩子的情况与左孩子的情况是对称的,只需将左孩子中的right换成left即可。
RB_INSERT_FIXUP(T,z) while color[parent[z]] = RED do if parent[z] == left[parent[parent[z]]] then y = right[parent[parent[z]]] if color[y] == RED //情况1,z的叔叔为红色 then color[parent[z]] = BLACK color[y] = BLACK color[parent[parent[z]]=RED z= parent[parent[z]] else if z == right[parent[z]] //情况2,z的叔叔为黑色,z为右孩子 then z = parent[z] LEFT_ROTATE(T,z) color[parent[z]]=BLACK //情况3,z的叔叔为黑色,z为左孩子 color[parent[parent[z]] = RED RIGHT_ROTATE(T, parent[parent[z]]) else (same as then clause with “right” and “left” exchanged) color(root(T)) = BLACK; //将根结点设置为黑色
4、删除
删除过程最复杂,看了好多遍才明白个大概,需要反复看,多想删除过程中会破坏哪些性质,然后又针对性的去调整。
红黑树删除结点过程是在二叉查找树删除结点过程的基础改进的。与二叉查找树类似,删除的结点分为三种情况:<1>无左右孩子、<2>有左孩子或者右孩子、<3>既有树=左孩子又有右孩子。删除过程可以参考前一篇日志:http://www.cnblogs.com/Anker/archive/2013/01/28/2880581.html。红黑树在删除结点后需要检查是否破坏了红黑树的性质。如果删除的结点y是红色的,则删除后的树仍然是保持红黑树的性质,因为树中各个结
点的黑高度没有改变,不存在两个相邻(父结点和子结点)的红色结点,y是红色不可能是根,所有根仍然是黑色。如果删除的结点z是黑色的,则这个是破坏了红黑树的性质,需要调用RB_DELETE_FIXUP进行调整。从删除
结点y的唯一孩子结点x或者是NIL处开始调整。书中给出了RB_DELETE的伪代码:
1 RB_DELETE(T,z) 2 if left[z] ==NIL or right[z] == NIL 3 then y=z 4 else y=TREE_SUCCESSOR(z) 5 if left[y] != NIL 6 then x=left[y] 7 else x=right[y] 8 parent[x] = parent[y] 9 if p[y] ==NIL 10 then root[T] =x 11 else if y = left[[prarnt[y]] 12 then left[parent[y]] = x 13 else right[parent[y]] =x 14 if y!=z 15 then key[z] = key[y] 16 copy y's data into z 17 if color[y] == BLACK //当被删除结点为黑色时候进行调整 18 then RB_DELETE_FIXUP(T,x) 19 return y
书中分析了被删除结点y是黑色会产生的问题:首先,如果y是根,而y的一个红色孩子变成了新根,则违反了性质2。其次,如果x和parent[y](此时parent[x] = parent[y])都是红色,就违反了性质4。第三,删除y将会导致先前包含y的任何路径上黑结点个数减少1,违反了性质5。书中给出了解决第三个问题的办法:将结点x设为还有额外的一重黑色(此处看的不是很明白,我的理解是是不管是x是什么颜色,将x增加了额外一重黑色,这样可以保证黑结点数目增加1个),即将任意包含结点x的路径上黑结点个数加1,这样可以保证性质5成立。当将黑色结点y被删除时,将其黑色“下推”至其子结点,导致问题变成为结点x可能即不是红,又不是黑,从而违反性质1。因为给x增加了一种颜色,即结点x是双重黑色或者是红黑色。这样就分别给包含x的路径上黑结点个数贡献2个或1个。但是x的color属性仍然是RED(如果x是红黑的)或BLACK(如果x是双重黑色)。换而言之,一个结点额外的黑色反映在x指向它,而不是它的color属性。
过程RB_DELETE_FIXUP恢复性质1,2,4。对于恢复性质2、4很简单,因为x是红色,所有直接将x结点着为黑色即可。书中着重介绍了如何恢复性质1。此时x是黑色,需要根据x是左孩子还是右孩子两种情况进行恢复,因为左右是对称的,书中只给出了x是左孩子的恢复过程。将x作为第一个额外的黑色结点,从x结点开始循环,将额外的黑色结点沿着树向上移,直到:
(1)x指向一个红黑结点,此时将x单独着为黑色。
(2)x指向根,这时可以简单地消除那个额外的黑色,或者
(3)做必要的旋转和颜色改变
在循环过程中,x总是指向具有双重黑色的那个非根结点。设w是x的兄弟结点,因为x是双重黑色的,故w不可能是NIL。书中分四种情况讨论:
情况1:x的兄弟w是红色的
此时因为x是双重黑色,贡献两个黑色结点,所有w必有黑色孩子。此时将w着为黑色,parent[x]为红色,在对parent[x]做一次左旋转。此时x的新兄弟w是黑色,这样将情况1转换为情况2、3或4。情况1的处理过程下图所示: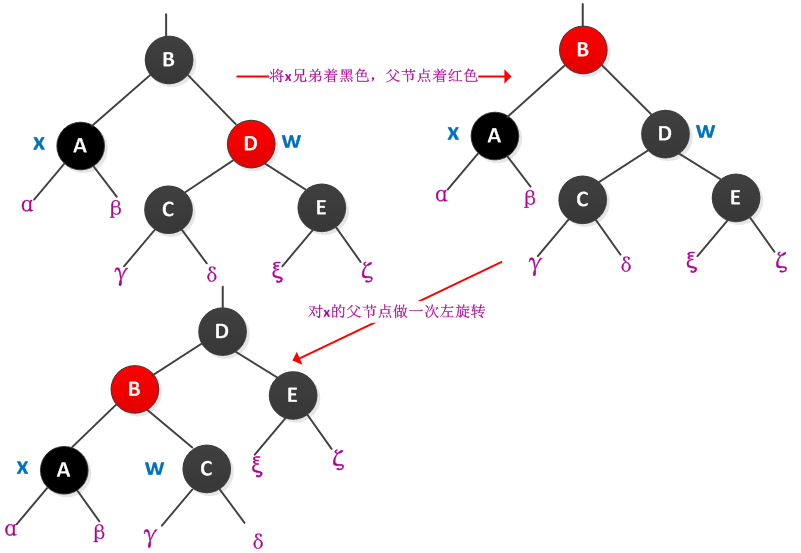
情况2:x的兄弟w是黑色的,而且w的两个孩子都是黑色的。
处理过程是从x和w上去掉一重黑色,即x只有一重黑色而w着为红色,给x的父节点parent[x]添加额外黑色。处理过程如下图所示: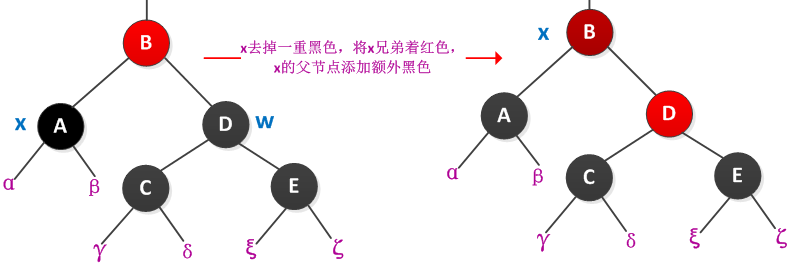
情况3:x的兄弟w是黑色的,w的左孩子是红色的,右孩子是黑色的
交换w和其左孩子left[w]的颜色,并对w进行右旋转。旋转后x的新兄弟w是一个有红色右孩子的黑结点,转换成了情况4。处理过程如下图所示: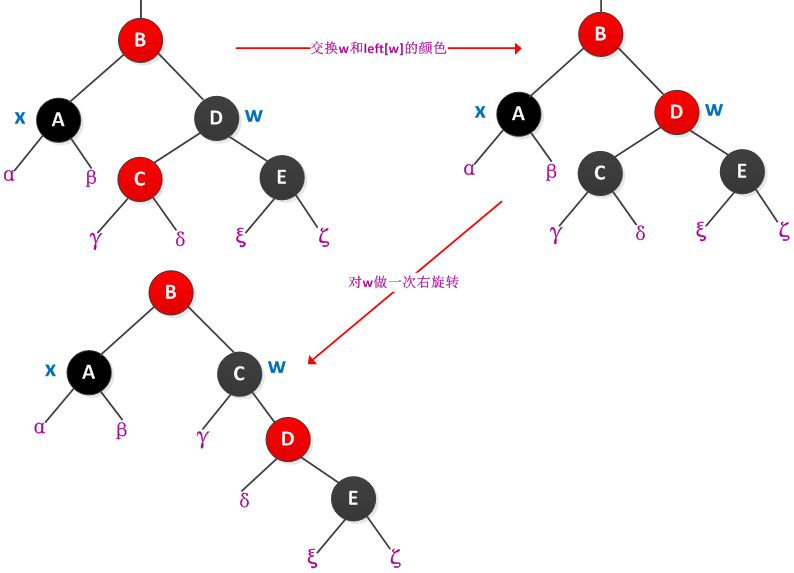
情况4:x的兄弟w是黑色的,而且w的右孩子是红色的。
执行过程是将w的颜色设置为parent[x]的颜色,将parent[x]的颜色设置为黑色,将w的右孩子着为黑色,然后在parent[x]做一次右旋,最后将x设置为根root。处理过程如下图所示:
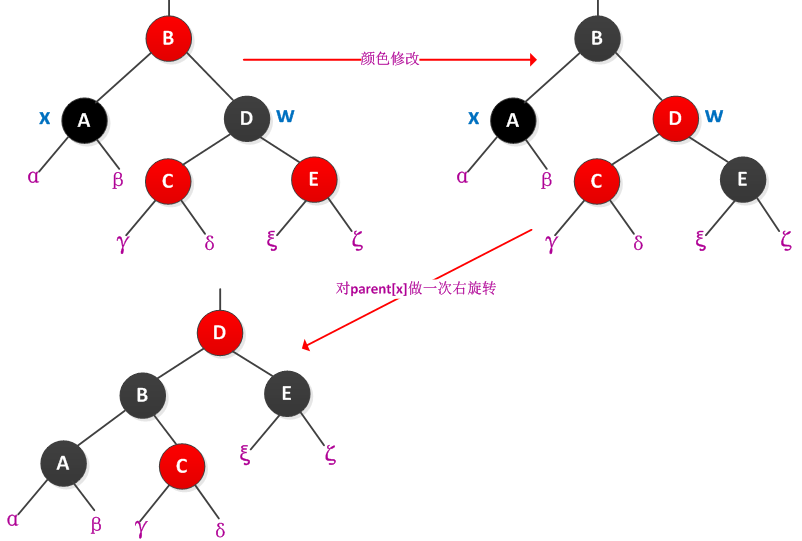
书中给出了RB_DELETE_FIXUP的伪代码:
1 RB_DELETE_FIXUP(T,x) 2 while x!= root[T] and color[x] ==BLACK 3 do if x == left[parent[x]] 4 then w = right[parent[x]] 5 if color[w] == RED //case 1 x的兄弟w是红色的 6 then color[w] = BLACK 7 color[parent[x]] = RED 8 LEFT_ROTATE(T,PARENT[x]) 9 w = right[parent[x]] 10 if color[left[w]] == BLACK and color[right[w]] = BLACK 11 then color[w] = RED //case 2 12 x = parent[x] 13 else if color[right[w]] =BLACK 14 then color[left[w]] = BLACK //case 3 15 color[w] = RED 16 RIGHT_ROTATE(T,w) 17 w = right[parent[x]] 18 color[w] = color[parent[x]] //case 4 19 color[parent[x]] = BLACK 20 color[right[w]] = BLACK 21 LEFT_ROTATE(T,parent[x]) 22 x=root(T) 23 else(same as then clasue with “right” and “left” exchanged) 24 color[x]=BLACK




