算法导论 第三部分——基本数据结构——栈、队列、链表、散列表
一、栈,队列,链表
栈是后进先出,而队列则是FIFO
栈的基本操作:
#include<stack>
stack<type> s; s.push(data_a); s.push(data_b); s.top(); // 返回一个type类型的值 s.pop(); // 只弹出,不返回值 是个void函数 s.empty(); s.size();
queue的基本操作:
#include<queue> queue<type> q; q.push(data_a); q.empty(); q.size(); q.pop(); q.front(); q.back();
list的基本操作:
#include<list> list<type> l; list<type> :: iterator first,last; l.insert(l.begin(),data_a); // 在链表的首插入元素 l.push_back(data_b); // 在链尾插入元素 l.push_front(data_c); // 在链表的首插入元素 l.clear(); // 清空链表 l.erase(iterator); l.erase(begin,end);
l.reverse(); l.sort(); //链表中的元素排序 //当元素是string或者其他类型时,需要重载sort函数 //https://msdn.microsoft.com/en-us/library/w56d4y5z.aspx?cs-save-lang=1&cs-lang=cpp#code-snippet-3
set,unordered_set,multi_set的基本操作
//set中相同元素只能存放一个,而multiset中可以存放多个 // 需要包含头文件 #include<set> set<int> in; in.insert(9); in.erase(10); in.count(9); // 9在in中的个数,如果是set的话只能是0或者1,multiset则可以使多个 set<int>::iterator p = in.find(9); //9 的指针 p++; // 指向下一个元素,但是不能写成 p=p+1 in.size(); //元素的个数,multiset 可以重复的
//unordered_set和set相同,#include<unordered_set>,相同元素只能存放一个,但是存放的数据是没有顺序的
// 或者说是按照先放进去的数据在头,后放进的在尾 ,而不是从小到大排序的
map的基本操作
#include<map> using namespace std; map<int,int> m; m[4] =3; //相当于插入一个元素 cout<<m[0]<<endl; // 访问一个没有的元素会默认插入一个元素 m.insert(make_pair(5,4)); // 插入一个元素 map<int,int>::iterator p = m.find(4); //返回一个指针 m.clear(); m.size(); m.begin();
二、散列表
散列表对应着STL中的map,map中一个key只能映射一个value。
部分转载自:http://www.cnblogs.com/Anker/archive/2013/01/27/2879150.html
1、直接寻址
当关键字的的全域(范围)U比较小的时,直接寻址是简单有效的技术,一般可以采用数组实现直接寻址表,数组下标对应的就是关键字的值,即具有关键字k的元素被放在直接寻址表的槽k中。
直接寻址表的字典操作实现比较简单,直接操作数组即可以,只需O(1)的时间。
2、散列表
直接寻址表的不足之处在于当关键字的范围U很大时,在计算机内存容量的限制下,构造一个存储|U|大小的表不太实际。当存储在字典中的关键字集合K比所有可能的关键字域U要小的多时,散列表需要的存储空间要比直接寻址表少的很多。散列表通过散列函数h计算出关键字k在槽的位置。散列函数h将关键字域U映射到散列表T[0....m-1]的槽位上。即h:U->{0,1...,m-1}。采用散列函数的目的在于缩小需要处理的小标范围,从而降低了空间的开销。
散列表存在的问题:两个关键字可能映射到同一个槽上,即碰撞(collision)。需要找到有效的办法来解决碰撞。
3、散列函数
好的散列函数的特点是每个关键字都等可能的散列到m个槽位上的任何一个中去,并与其他的关键字已被散列到哪一个槽位无关。多数散列函数都是假定关键字域为自然数N={0,1,2,....},如果给的关键字不是自然数,则必须有一种方法将它们解释为自然数。例如对关键字为字符串时,可以通过将字符串中每个字符的ASCII码相加,转换为自然数。书中介绍了三种设计方案:除法散列法、乘法散法和全域散列法。
(1)除法散列法
通过取k除以m的余数,将关键字k映射到m个槽的某一个中去。散列函数为:h(k)=k mod m 。m不应是2的幂,通常m的值是与2的整数幂不太接近的质数。
(2)乘法散列法
这个方法看的时候不是很明白,没有搞清楚什么意思,先将基本的思想记录下来,日后好好消化一下。乘法散列法构造散列函数需要两个步骤。第一步,用关键字k乘上常数A(0<A<1),并抽取kA的小数部分。然后,用m乘以这个值,再取结果的底。散列函数如下:h(k) = m(kA mod 1)。
(3)全域散列
给定一组散列函数H,每次进行散列时候从H中随机的选择一个散列函数h,使得h独立于要存储的关键字。全域散列函数类的平均性能是比较好的。
4、碰撞处理
通常有两类方法处理碰撞:开放寻址(Open Addressing)法和链接(Chaining)法。前者是将所有结点均存放在散列表T[0..m-1]中;后者通常是把散列到同一槽中的所有元素放在一个链表中,而将此链表的头指针放在散列表T[0..m-1]中。
(1)开放寻址法
所有的元素都在散列表中,每一个表项或包含动态集合的一个元素,或包含NIL。这种方法中散列表可能被填满,以致于不能插入任何新的元素。在开放寻址法中,当要插入一个元素时,可以连续地检查或探测散列表的各项,直到有一个空槽来放置待插入的关键字为止。有三种技术用于开放寻址法:线性探测、二次探测以及双重探测。
优点:
不用指针,而是计算出要存取的槽序列。不用存储指针而节省空间,这样就可以提供更多的槽,潜在地减少了冲突,提高了检索速度。
<1>线性探测
给定一个普通的散列函数h':U —>{0,1,.....,m-1},线性探测方法采用的散列函数为:h(k,i) = (h'(k)+i)mod m,i=0,1,....,m-1
探测时从i=0开始,首先探查T[h'(k)],然后依次探测T[h'(k)+1],…,直到T[h'(k)+m-1],此后又循环到T[0],T[1],…,直到探测到T[h'(k)-1]为止。探测过程终止于三种情况:
(1)若当前探测的单元为空,则表示查找失败(若是插入则将key写入其中);
(2)若当前探测的单元中含有key,则查找成功,但对于插入意味着失败;
(3)若探测到T[h'(k)-1]时仍未发现空单元也未找到key,则无论是查找还是插入均意味着失败(此时表满)。
线性探测方法较容易实现,但是存在一次群集问题,即连续被占用的槽的序列变的越来越长。采用例子进行说明线性探测过程,已知一组关键字为(26,36,41,38,44,15,68,12,6,51),用除余法构造散列函数,初始情况如下图所示:

散列过程如下图所示:

线性探测的元素删除:
首先得明白hash_search()中search一个元素的操作方法
HASH_SEARSH(T,k){ i=0; repeart: j=h(k,i); if(T[j]==k) return j; i++; until T[j]=NIL or i==m return NIL; }
如果删除一个元素之后就将该位置为NIL,则在search的时候会出现 存在某个元素再要删除元素之后,现在search到NIL就结束了返回NIL。
正确的做法,在槽i置一个特定的值DELETED代替NIL来标记该槽。
<2>二次探测
二次探测法的探查序列是:
h(k,i) =(h'(k)+i*i)%m ,0≤i≤m-1
初次的探测位置为T[h'(k)],后序的探测位置在次基础上加一个偏移量,该偏移量以二次的方式依赖于i。该方法的缺陷是不易探查到整个散列空间。
<3>双重散列
该方法是开放寻址的最好方法之一,因为其产生的排列具有随机选择的排列的许多特性。采用的散列函数为:h(k,i)=(h1(k)+ih2(k)) mod m。其中h1和h2为辅助散列函数。初始探测位置为T[h1(k)],后续的探测位置在此基础上加上偏移量h2(k)模m。
(2)链接法
将所有关键字为同义词的结点链接在同一个链表中。若选定的散列表长度为m,则可将散列表定义为一个由m个头指针组成的指针数组T[0..m-1]。凡是散列地址为i的结点,均插入到以T[i]为头指针的单链表中。T中各分量的初值均应为空指针。在拉链法中,装填因子α可以大于1,但一般均取α≤1。
举例说明链接如下图所示: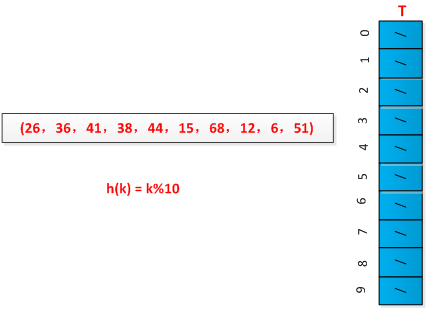
最终结果如下图所示:




