线性模型学习笔记
注:该文是根据开智学堂数据科学入门班的讲课内容整理而成,主讲人是肖凯老师。
线性模型
主要学习用 statsmodels 模块进行线性回归、逻辑回归和时间序列分析。
线性模型基本概念
多个因素的定量化计算,是线性模型的最主要用途。
由上式,有两个因素 \(x_{1}\) 和 \(x_{2}\) 同时影响 y,前面的系数 \(\beta_{1}\) 和 \(\beta_{2}\) 就是这个因素影响的力度大小,可以认为是方向和强度,负的就是负影响,正的就是正影响。\(\beta_{0}\)就是当\(x_{1}\)、\(x_{2}\) 都取 0 时,y 也有个正常的期望值。还有一些因素会影响 y,可以认为是个随机项,或者噪音,也就是不在方程里考虑,不在思维框架里考虑,但它仍然会影响 y,只是影响比较小,就是 \(\epsilon\)。
线性模型就是衡量不同因素之间的关系,并且把它们定量化。
方程是我们的假设方程。
方程的左边 y 是目标变量,或依赖变量,英文叫做 dependent variables,是我们希望去解释的变量,即被解释变量。
方程的右边 x 是自变量,或解释变量,explanatory variables。
通常左边只有一个 y,右边有多个 x。
求解的时候跟线性拟合非常相似,要找到一个方程,使误差最小。求解的方法跟最优化的方法一样,采用 ordinary least squares,即最小二乘法。
import statsmodels.api as sm # 基本 API
import statsmodels.formula.api as smf # 公式 API
import statsmodels.graphics.api as smg # 图形界面 API
import patsy # 主要类似 R 语言的公式转成 statsmodels 可以识别的形式
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy import stats
import seaborn as sns
np.random.seed(123456789)
y = np.array([1, 2, 3, 4, 5])
x1 = np.array([6, 7, 8, 9, 10])
x2 = np.array([11, 12, 13, 14, 15])
X = np.vstack([np.ones(5), x1, x2, x1*x2]).T
print X
[[ 1. 6. 11. 66.]
[ 1. 7. 12. 84.]
[ 1. 8. 13. 104.]
[ 1. 9. 14. 126.]
[ 1. 10. 15. 150.]]
X 为构造的矩阵,线性回归中的自变量,每一个行是一个样本,每一列可认为是一个变量。全为 1 的变量可认为是截距项,x1*x2 是 x1 和 x2 的交互项。共有 3 个变量影响 y。
把 X 当作自变量,y 当作因变量,可以用 numpy 中最小二乘 np.linalg.lstsq 求对应的系数,跟最优化中的求拟合 opt.minimize 同样的原理。
beta, res, rank, sval = np.linalg.lstsq(X, y)
print beta
[ -5.55555556e-01 1.88888889e+00 -8.88888889e-01 -1.33226763e-15]
这里使用 statsmodels 用的模块来做多元线性回归,结果跟上面差不多。
model = sm.OLS(y, X) # OLS 是普通最小二乘,sm 中还有很多其它方法解决不同的问题
result = model.fit() # 做拟合
print result.params # 对应的各个变量的权重
[ -5.55555556e-01 1.88888889e+00 -8.88888889e-01 -1.22124533e-15]
还可以采取公式的方式。
data = {"y": y, "x1": x1, "x2": x2}
df_data = pd.DataFrame(data)
model = smf.ols("y ~ 1 + x1 + x2 + x1:x2", df_data) # 1 表示截距,默认是有截距,x1:x2 交互项中的冒号是相乘
result = model.fit() # 做拟合
print result.params
Intercept -5.555556e-01
x1 1.888889e+00
x2 -8.888889e-01
x1:x2 -1.221245e-15
dtype: float64
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 1.000
Model: OLS Adj. R-squared: 1.000
Method: Least Squares F-statistic: 4.723e+27
Date: Sat, 18 Jun 2016 Prob (F-statistic): 2.12e-28
Time: 00:19:04 Log-Likelihood: 150.48
No. Observations: 5 AIC: -295.0
Df Residuals: 2 BIC: -296.1
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept -0.5556 7.42e-14 -7.49e+12 0.000 -0.556 -0.556
x1 1.8889 2.77e-13 6.82e+12 0.000 1.889 1.889
x2 -0.8889 9.43e-14 -9.43e+12 0.000 -0.889 -0.889
x1:x2 -1.221e-15 8.7e-15 -0.140 0.901 -3.86e-14 3.62e-14
==============================================================================
Omnibus: nan Durbin-Watson: 0.034
Prob(Omnibus): nan Jarque-Bera (JB): 0.319
Skew: 0.407 Prob(JB): 0.853
Kurtosis: 2.069 Cond. No. 8.37e+17
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The smallest eigenvalue is 8.82e-32. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
公式构造还有其它的形式,如下所示,毋须多言。
from collections import defaultdict
data = defaultdict(lambda: np.array([1,2,3]))
patsy.dmatrices("y ~ a", data=data)[1].design_info.term_names # design_info.term_names 这些东西的含义不用在意,只看前面的公式表示就行
['Intercept', 'a']
patsy.dmatrices("y ~ 1 + a + b", data=data)[1].design_info.term_names
['Intercept', 'a', 'b']
patsy.dmatrices("y ~ -1 + a + b", data=data)[1].design_info.term_names # -1 表示不要截距项
['a', 'b']
patsy.dmatrices("y ~ a * b", data=data)[1].design_info.term_names # a * b 表示有 a 有 b 有 a*b
['Intercept', 'a', 'b', 'a:b']
patsy.dmatrices("y ~ a * b * c", data=data)[1].design_info.term_names
['Intercept', 'a', 'b', 'a:b', 'c', 'a:c', 'b:c', 'a:b:c']
patsy.dmatrices("y ~ a * b * c - a:b:c", data=data)[1].design_info.term_names # 只需要两两相乘,不需要三个相乘
['Intercept', 'a', 'b', 'a:b', 'c', 'a:c', 'b:c']
data = {k: np.array([]) for k in ["y", "a", "b", "c"]}
patsy.dmatrices("y ~ a + b", data=data)[1].design_info.term_names # 这里的运算符 + 并不是表示 a 和 b 要加起来,只是表示有 a 有 b
['Intercept', 'a', 'b']
patsy.dmatrices("y ~ I(a + b)", data=data)[1].design_info.term_names # 如果真要 a+b,I 类似转义符号
['Intercept', 'I(a + b)']
patsy.dmatrices("y ~ I(a**2)", data=data)[1].design_info.term_names
['Intercept', 'I(a ** 2)']
patsy.dmatrices("y ~ np.log(a) + b", data=data)[1].design_info.term_names # 还可以做数学转换
['Intercept', 'np.log(a)', 'b']
z = lambda x1, x2: x1+x2
patsy.dmatrices("y ~ z(a, b)", data=data)[1].design_info.term_names # 把 z 放到公式里
['Intercept', 'z(a, b)']
前面的都是数值变量,分类变量怎么在公式里体现呢?
data = {"y": [1, 2, 3], "a": [1, 2, 3]}
patsy.dmatrices("y ~ - 1 + a", data=data, return_type="dataframe")[1]
| a | |
|---|---|
| 0 | 1.0 |
| 1 | 2.0 |
| 2 | 3.0 |
patsy.dmatrices("y ~ - 1 + C(a)", data=data, return_type="dataframe")[1]
| C(a)[1] | C(a)[2] | C(a)[3] | |
|---|---|---|---|
| 0 | 1.0 | 0.0 | 0.0 |
| 1 | 0.0 | 1.0 | 0.0 |
| 2 | 0.0 | 0.0 | 1.0 |
data = {"y": [1, 2, 3], "a": ["type A", "type B", "type C"]}
patsy.dmatrices("y ~ - 1 + a", data=data, return_type="dataframe")[1]
| a[type A] | a[type B] | a[type C] | |
|---|---|---|---|
| 0 | 1.0 | 0.0 | 0.0 |
| 1 | 0.0 | 1.0 | 0.0 |
| 2 | 0.0 | 0.0 | 1.0 |
patsy.dmatrices("y ~ - 1 + C(a, Poly)", data=data, return_type="dataframe")[1] # C 符号转成高次函数
| C(a, Poly).Constant | C(a, Poly).Linear | C(a, Poly).Quadratic | |
|---|---|---|---|
| 0 | 1.0 | -7.071068e-01 | 0.408248 |
| 1 | 1.0 | -5.551115e-17 | -0.816497 |
| 2 | 1.0 | 7.071068e-01 | 0.408248 |
pasty 的作用是什么?有哪几种方法构造线性回归模型?模型 y = 1 + x_1 + x_2 + x_1 * x_2 用 pasty 怎么表示?
pasty 是把类似 R 语言的公式转成 statsmodels 可以识别的形式。
可以使用 numpy.linalg.lstsq,或 scipy.optimize.minimize,或 statsmodels.OLS(y, X),或 statsmodels.formula.api.ols("y ~ 1 + x1 + x2 + x1:x2", df_data)。
模型 y = 1 + x_1 + x_2 + x_1 * x_2 用 pasty 表示方法如下:
from collections import defaultdict
data = defaultdict(lambda: np.array([1,2,3]))
patsy.dmatrices("y ~ x1 * x2", data=data)[1].design_info.term_names
['Intercept', 'x1', 'x2', 'x1:x2']
patsy.dmatrices("y ~ 1 + x1 + x2 + x1:x2", data=data)[1].design_info.term_names
['Intercept', 'x1', 'x2', 'x1:x2']
线性回归
上面介绍了线性模型基本概念,这里介绍线性回归。
线性回归指方程左边的 y 取实数值,即 (\(-\infty,+\infty\)),如果右边只有一个 x,就是一元线性回归,当 x 变化时,y 也随着变化,x 和 y 呈线性关系,可以用直线表示;如果 x 有多个,可以用超平面表示。线性回归的线性,指 x 和 y 呈线性关系,回归指 y 是连续的数值。
看例子:
np.random.seed(123456789)
N = 100
x1 = np.random.randn(N) # 自变量
x2 = np.random.randn(N)
data = pd.DataFrame({"x1": x1, "x2": x2})
def y_true(x1, x2):
return 1 + 2 * x1 + 3 * x2 + 4 * x1 * x2
data["y_true"] = y_true(x1, x2) # 因变量
e = np.random.randn(N) # 标准正态分布
data["y"] = data["y_true"] + e # 加些噪音,加些扰动,噪音是符合标准正态分布的
data.head()
| x1 | x2 | y_true | y | |
|---|---|---|---|---|
| 0 | 2.212902 | -0.474588 | -0.198823 | -1.452775 |
| 1 | 2.128398 | -1.524772 | -12.298805 | -12.560965 |
| 2 | 1.841711 | -1.939271 | -15.420705 | -14.715090 |
| 3 | 0.082382 | 0.345148 | 2.313945 | 1.190283 |
| 4 | 0.858964 | -0.621523 | -1.282107 | 0.307772 |
y_true 列是真正的 y,y 列是加了噪音的 y。造了该数据是为了做线性回归,有两个自变量,即二元线性回归。加噪音是为了模仿真实场景,真实场景中自变量和因变量的关系往往不是固定的,是有随机扰动的。目的是只给你看 y、x1 和 x2,你要反推回 y 和 x1 和 x2 之间的函数关系,假定这个函数关系是线性的。
只有 x1、x2 和 y 三列数据的情况下,先画个散点图看下。
fig, axes = plt.subplots(1, 2, figsize=(8, 4))
axes[0].scatter(data["x1"], data["y"])
axes[1].scatter(data["x2"], data["y"])
fig.tight_layout();
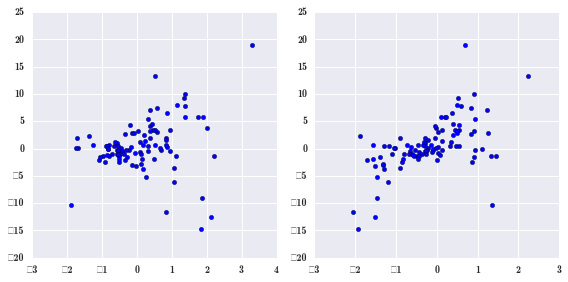
大体来看,存在一定的相关性,但由于噪音的存在,相关性不明显。
使用上面介绍的 smf.ols 做线性回归。
model = smf.ols("y ~ x1 + x2", data) # 这里没有写截距,截距是默认存在的
result = model.fit()
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.380
Model: OLS Adj. R-squared: 0.367
Method: Least Squares F-statistic: 29.76
Date: Sat, 18 Jun 2016 Prob (F-statistic): 8.36e-11
Time: 07:41:16 Log-Likelihood: -271.52
No. Observations: 100 AIC: 549.0
Df Residuals: 97 BIC: 556.9
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 0.9868 0.382 2.581 0.011 0.228 1.746
x1 1.0810 0.391 2.766 0.007 0.305 1.857
x2 3.0793 0.432 7.134 0.000 2.223 3.936
==============================================================================
Omnibus: 19.951 Durbin-Watson: 1.682
Prob(Omnibus): 0.000 Jarque-Bera (JB): 49.964
Skew: -0.660 Prob(JB): 1.41e-11
Kurtosis: 6.201 Cond. No. 1.32
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
上面的 summary 回归结果主要看几个地方:R-squared 在统计学里叫判定系数,或决定系数,也称拟合优度,值在 0 到 1 之间,值越大,表示这个模型拟合的越好,这里 0.38 就拟合的不好;还要看系数对应的值 coef,这里有三个 Intercept、x1 和 x2,std err 是标准误,还有 t 和 P,这是对每个系数做了个统计推断,统计推断的原假设是系数为 0,表示该系数在模型里不用存在,不用理解原理和具体过程,可以直接看 P 值,P 值如果很小,就推断原假设,即其实系数不为 0,该变量在模型中应该是存在的,如上面的 summary 结果,x1 和 x2 的 P 值都很小,说明这两个自变量在模型里都是有意义的,都应该存在模型里。有些回归问题中,P 值比较大,那么对应的变量就可以扔掉。
初学者只关注 summary 结果中的判定系数,各自变量对应的系数值及 P 值即可。
print result.rsquared
0.380253832551
还要看对应的残差,残差表示真实值和模型拟合值的距离。这里有 100 个数据,也就有 100 个残差。
result.resid.shape
(100,)
result.resid.head() # 残差,result 的 resid 属性
0 -3.370455
1 -11.153477
2 -11.721319
3 -0.948410
4 0.306215
dtype: float64
理论上残差应该服从正态分布,可以检验下。
z, p = stats.normaltest(result.resid.values) # 正态性检验,原假设是数据服从正态性
print p
4.6524990253e-05
p 值很小,拒绝原假设,即残差不服从正态分布。
除了使用正态性检验 stats.normaltest,还可以画 QQ 图。QQ 图里残差如果排成 45 度的斜线,表示数据是服从理论分布的。
fig, ax = plt.subplots(figsize=(8, 4))
smg.qqplot(result.resid, ax=ax)
fig.tight_layout()

这里残差数据就不服从正态分布。
现在上面的模型做完之后有几个不好的地方,一个是残差不服从理论假定,说明残差里有些东西,应该放到模型里,结果跑到残差里来了;第二个是 R-squared 比较低,意味着有很多东西没法解释,y 里面应该有很多东西可以用 x 解释,但这里只有 38% 被 x 解释,很多东西在残差里。所以用上面的公式 y ~ x1 + x2 来拟合是有问题的。所以这里改下公式,y 除了是由 x1 和 x2 决定的,还应该加上交互项。
model = smf.ols("y ~ x1 + x2 + x1:x2", data)
result = model.fit()
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.955
Model: OLS Adj. R-squared: 0.954
Method: Least Squares F-statistic: 684.5
Date: Sat, 18 Jun 2016 Prob (F-statistic): 1.21e-64
Time: 08:31:46 Log-Likelihood: -140.01
No. Observations: 100 AIC: 288.0
Df Residuals: 96 BIC: 298.4
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 0.8706 0.103 8.433 0.000 0.666 1.076
x1 1.9693 0.108 18.160 0.000 1.754 2.185
x2 2.9670 0.117 25.466 0.000 2.736 3.198
x1:x2 3.9440 0.112 35.159 0.000 3.721 4.167
==============================================================================
Omnibus: 2.950 Durbin-Watson: 2.072
Prob(Omnibus): 0.229 Jarque-Bera (JB): 2.734
Skew: 0.327 Prob(JB): 0.255
Kurtosis: 2.521 Cond. No. 1.38
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
R-squared 变成 0.95,模型非常好,再看几个自变量对应的值,P 值都很小,表示几个项都应该在模型里存在。
再来看残差的正态性检验。
z, p = stats.normaltest(result.resid.values)
p
0.22874710482505187
fig, ax = plt.subplots(figsize=(8, 4))
smg.qqplot(result.resid, ax=ax)
fig.tight_layout()
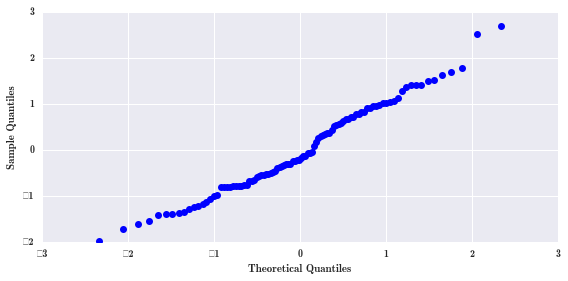
接近 45 度的斜线,可以认为残差服从理论分布。
这就是线性回归的例子,可以看到,估计出的几个自变量系数值 0.8706、1.9693、2.9670 和 3.9440 和真实值 1、2、3、4 还是比较接近的,估计结果很好。估计值与真实值不一样是因为我们加了噪音在数据中。
可以把这个结果再画个图来研究下。可以用上面产生的模型做新的预测。
x = np.linspace(-1, 1, 50) # 建立新的 data
X1, X2 = np.meshgrid(x, x) # 转成二维
new_data = pd.DataFrame({"x1": X1.ravel(), "x2": X2.ravel()})
y_pred = result.predict(new_data) # 使用上面拟合得到的模型
y_pred.shape
(2500,)
y_pred = y_pred.reshape(50, 50)
fig, axes = plt.subplots(1, 2, figsize=(12, 5), sharey=True)
def plot_y_contour(ax, Y, title):
c = ax.contourf(X1, X2, Y, 15, cmap=plt.cm.RdBu) # 二元,正好用平面图表示,y 用颜色表示
ax.set_xlabel(r"$x_1$", fontsize=20)
ax.set_ylabel(r"$x_2$", fontsize=20)
ax.set_title(title)
cb = fig.colorbar(c, ax=ax)
cb.set_label(r"$y$", fontsize=20)
plot_y_contour(axes[0], y_true(X1, X2), "true relation") # 真实值
plot_y_contour(axes[1], y_pred, "fitted model") # 拟合模型计算的值
fig.tight_layout()

上面两图没什么区别,表明拟合的很好。
理解了线性回归,再看个例子。statsmodels 可以读 R 语言里的数据,比如冰淇淋数据,如果对数据不了解,可以用 print(dataset.doc) 查看数据信息。
dataset = sm.datasets.get_rdataset("Icecream", "Ecdat")
print dataset.title
Ice Cream Consumption
dataset.data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 30 entries, 0 to 29
Data columns (total 4 columns):
cons 30 non-null float64
income 30 non-null int64
price 30 non-null float64
temp 30 non-null int64
dtypes: float64(2), int64(2)
memory usage: 1.0 KB
dataset.data.head()
| cons | income | price | temp | |
|---|---|---|---|---|
| 0 | 0.386 | 78 | 0.270 | 41 |
| 1 | 0.374 | 79 | 0.282 | 56 |
| 2 | 0.393 | 81 | 0.277 | 63 |
| 3 | 0.425 | 80 | 0.280 | 68 |
| 4 | 0.406 | 76 | 0.272 | 69 |
model = smf.ols("cons ~ -1 + price + temp", data=dataset.data) # 建立价格、气温和销量的关系,二元回归,不要截距项
result = model.fit()
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: cons R-squared: 0.986
Model: OLS Adj. R-squared: 0.985
Method: Least Squares F-statistic: 1001.
Date: Sat, 18 Jun 2016 Prob (F-statistic): 9.03e-27
Time: 09:04:54 Log-Likelihood: 51.903
No. Observations: 30 AIC: -99.81
Df Residuals: 28 BIC: -97.00
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
price 0.7254 0.093 7.805 0.000 0.535 0.916
temp 0.0032 0.000 6.549 0.000 0.002 0.004
==============================================================================
Omnibus: 5.350 Durbin-Watson: 0.637
Prob(Omnibus): 0.069 Jarque-Bera (JB): 3.675
Skew: 0.776 Prob(JB): 0.159
Kurtosis: 3.729 Cond. No. 593.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
R-squared 为 0.98,拟合效果不错。price 和 temp 的 P 值很小,都是很显著的,表示应该放在模型里。
coef 的解释为,temp 每增加 1 个单位,对应的 y 应该增加 0.003 个单位,price 每增加 1 个单位,对应的销售增加 0.72 个单位。
再看下对应的图形。
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
smg.plot_fit(result, 0, ax=ax1)
smg.plot_fit(result, 1, ax=ax2)
fig.tight_layout()

从图中可以看到,温度增加,销售增加,趋势是比较明显的,但价格变化,销售并没怎么变,这就带来个疑问,为什么价格变化,销售没什么变化呢?有个可能是,价格变动的范围太小了,0.26~0.29,价格变化不大,所以价格变化并没有引起销售明显的变化。还有个疑点,是上面的 coef 中,price 跟跟销售的关系竟然是正向的,按常理,价格增加销售应该下降,这是比较奇怪的,可以进一步研究相关数据。
也可用 seaborn 画变量关系。
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
sns.regplot("price", "cons", dataset.data, ax=ax1);
sns.regplot("temp", "cons", dataset.data, ax=ax2);
fig.tight_layout()
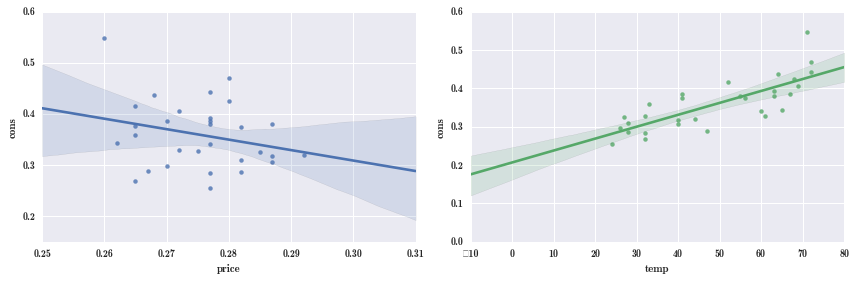
注意到温度跟消费呈正向关系,而 price 和 cons 又呈反向关系了,为什么会这样?因为前面的图是把消费里面关于温度的影响给去掉了,也就是 cons 中没有考虑 temp 的影响,单跟 price 的相关图,而这里左图 cons 是包含了 temp 的影响,这点要注意下,这是个单纯的散点图,所以才看到反向影响,price 左边 cons 高,可能是温度 temp 高,price 右边可能是温度较低。所以,一元回归,只看一个变量,背后可能隐藏了第三者,多元回归就是为了去除第三者的影响,散点图可以做探索时看,但不能做为模型依据,模型依据还是要看 summary 中对应的系数,这些系数抛掉了其它因素的影响。
模型自变量的 P 值比较大说明了什么?模型拟合剩下的残差有哪些用处?R 平方值是什么意思?qqplot 是什么图?
P 值较大,说明对应的自变量系数为 0,对于因变量 y 来说就没什么意义,可以把该自变量删掉。
残差表示真实值和模型拟合值的距离。比较两个模型的拟合效果,可以通过比较它们的残差平方和的大小来确定,残差平方和越小的模型,拟合效果越好。
R 平方值在统计学里叫判定系数,或决定系数,也称拟合优度,值在 0 到 1 之间,值越大,表示这个模型拟合的越好。
qqplot 用于检验一个序列是否服从正态分布,用 \(Q-Q'\) 图与 y=x 比较,若基本吻合则序列服从正态分布,若相差较大则不服从正态分布。
Logistic 回归
线性回归的 y 是连续值,Logistic 回归是要解可能发生事件的概率这样的值。例如 x 可能是今天的温度、湿度,y 是下雨的概率。
y 是个概率,就必然在 0 到 1 这个区间,如果用线性回归来做,值在 (\(-\infty,+\infty\)),所以需要做些转换。
p 是求的概率,p/1-p 称为机率。
df = sm.datasets.get_rdataset("iris").data # 鸢尾花数据
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 150 entries, 0 to 149
Data columns (total 5 columns):
Sepal.Length 150 non-null float64
Sepal.Width 150 non-null float64
Petal.Length 150 non-null float64
Petal.Width 150 non-null float64
Species 150 non-null object
dtypes: float64(4), object(1)
memory usage: 5.9+ KB
df.Species.unique() # 花的种类
array(['setosa', 'versicolor', 'virginica'], dtype=object)
df_subset = df[(df.Species == "versicolor") | (df.Species == "virginica" )].copy() # 取个子集,相当于去掉了 setosa,因为这里只做二分类
df_subset.Species = df_subset.Species.map({"versicolor": 1, "virginica": 0}) # 做个映射,因为做分类时 y 要取数值
df_subset.rename(columns={"Sepal.Length": "Sepal_Length", "Sepal.Width": "Sepal_Width",
"Petal.Length": "Petal_Length", "Petal.Width": "Petal_Width"}, inplace=True) # 重命名,因为点号在 python 里有特殊意义
df_subset.head(3)
| Sepal_Length | Sepal_Width | Petal_Length | Petal_Width | Species | |
|---|---|---|---|---|---|
| 50 | 7.0 | 3.2 | 4.7 | 1.4 | 1 |
| 51 | 6.4 | 3.2 | 4.5 | 1.5 | 1 |
| 52 | 6.9 | 3.1 | 4.9 | 1.5 | 1 |
model = smf.logit("Species ~ Sepal_Length + Sepal_Width + Petal_Length + Petal_Width", data=df_subset)
result = model.fit() # 内部使用极大似然估计,所以会有结果返回,表示成功收敛
Optimization terminated successfully.
Current function value: 0.059493
Iterations 12
print(result.summary())
Logit Regression Results
==============================================================================
Dep. Variable: Species No. Observations: 100
Model: Logit Df Residuals: 95
Method: MLE Df Model: 4
Date: Sat, 18 Jun 2016 Pseudo R-squ.: 0.9142
Time: 10:21:54 Log-Likelihood: -5.9493
converged: True LL-Null: -69.315
LLR p-value: 1.947e-26
================================================================================
coef std err z P>|z| [95.0% Conf. Int.]
--------------------------------------------------------------------------------
Intercept 42.6378 25.708 1.659 0.097 -7.748 93.024
Sepal_Length 2.4652 2.394 1.030 0.303 -2.228 7.158
Sepal_Width 6.6809 4.480 1.491 0.136 -2.099 15.461
Petal_Length -9.4294 4.737 -1.990 0.047 -18.714 -0.145
Petal_Width -18.2861 9.743 -1.877 0.061 -37.381 0.809
================================================================================
summary 跟前面线性回归的 summary 是类似的,Pseudo R-squ. 称为伪 R 方,同 R 方拟合优度,这里 0.91 结果不错。
从 summary 中各自变量结果来看,Petal_Length 和 Petal_Width 的 P 值要显著些,预测时只需要这两个变量就行。
对于系数的影响 coef,因为 Logistic 回归是对线性组合做了映射,所以对系数的解释就不像线性回归那么简单明了。可以用 get_margeff 边际效能函数来看下,取导数的形式,即 x 变动多少,y 跟着变动多少。
print(result.get_margeff().summary())
Logit Marginal Effects
=====================================
Dep. Variable: Species
Method: dydx
At: overall
================================================================================
dy/dx std err z P>|z| [95.0% Conf. Int.]
--------------------------------------------------------------------------------
Sepal_Length 0.0445 0.038 1.163 0.245 -0.031 0.120
Sepal_Width 0.1207 0.064 1.891 0.059 -0.004 0.246
Petal_Length -0.1703 0.057 -2.965 0.003 -0.283 -0.058
Petal_Width -0.3303 0.110 -2.998 0.003 -0.546 -0.114
================================================================================
可以看到 y 随 Petal_Length 和 Petal_Width 变化而变化的范围较大。
model = smf.logit("Species ~ Petal_Length + Petal_Width", data=df_subset)
result = model.fit() # 重新拟合
Optimization terminated successfully.
Current function value: 0.102818
Iterations 10
print(result.summary())
Logit Regression Results
==============================================================================
Dep. Variable: Species No. Observations: 100
Model: Logit Df Residuals: 97
Method: MLE Df Model: 2
Date: Sat, 18 Jun 2016 Pseudo R-squ.: 0.8517
Time: 10:22:55 Log-Likelihood: -10.282
converged: True LL-Null: -69.315
LLR p-value: 2.303e-26
================================================================================
coef std err z P>|z| [95.0% Conf. Int.]
--------------------------------------------------------------------------------
Intercept 45.2723 13.612 3.326 0.001 18.594 71.951
Petal_Length -5.7545 2.306 -2.496 0.013 -10.274 -1.235
Petal_Width -10.4467 3.756 -2.782 0.005 -17.808 -3.086
================================================================================
print(result.get_margeff().summary())
Logit Marginal Effects
=====================================
Dep. Variable: Species
Method: dydx
At: overall
================================================================================
dy/dx std err z P>|z| [95.0% Conf. Int.]
--------------------------------------------------------------------------------
Petal_Length -0.1736 0.052 -3.347 0.001 -0.275 -0.072
Petal_Width -0.3151 0.068 -4.608 0.000 -0.449 -0.181
================================================================================
这里有两个系数,可以放到二维空间来表示,二维空间的模型会存在一个决策边界,即,当 Petal_Length 或 Petal_Width 大于某个值或小于某个值时,花的种类就不一样了,花的决策边界可以由 dy/dx 的值构造而成。
params = result.params
beta0 = -params['Intercept']/params['Petal_Width']
beta1 = -params['Petal_Length']/params['Petal_Width']
df_new = pd.DataFrame({"Petal_Length": np.random.randn(20)*0.5 + 5,
"Petal_Width": np.random.randn(20)*0.5 + 1.7})
df_new["P-Species"] = result.predict(df_new)
df_new["P-Species"].head(3)
0 0.995472
1 0.799899
2 0.000033
Name: P-Species, dtype: float64
df_new["Species"] = (df_new["P-Species"] > 0.5).astype(int)
df_new.head()
| Petal_Length | Petal_Width | P-Species | Species | |
|---|---|---|---|---|
| 0 | 4.717684 | 1.218695 | 0.995472 | 1 |
| 1 | 5.280952 | 1.292013 | 0.799899 | 1 |
| 2 | 5.610778 | 2.230056 | 0.000033 | 0 |
| 3 | 4.458715 | 1.907844 | 0.421614 | 0 |
| 4 | 4.822227 | 1.938929 | 0.061070 | 0 |
fig, ax = plt.subplots(1, 1, figsize=(8, 4)) # 定义画布
ax.plot(df_subset[df_subset.Species == 0].Petal_Length.values,
df_subset[df_subset.Species == 0].Petal_Width.values, 's', label='virginica') # 画真实数据
ax.plot(df_new[df_new.Species == 0].Petal_Length.values,
df_new[df_new.Species == 0].Petal_Width.values,
'o', markersize=10, color="steelblue", label='virginica (pred.)') # 画预测数据
ax.plot(df_subset[df_subset.Species == 1].Petal_Length.values,
df_subset[df_subset.Species == 1].Petal_Width.values, 's', label='versicolor') # 点图
ax.plot(df_new[df_new.Species == 1].Petal_Length.values,
df_new[df_new.Species == 1].Petal_Width.values,
'o', markersize=10, color="green", label='versicolor (pred.)')
_x = np.array([4.0, 6.1])
ax.plot(_x, beta0 + beta1 * _x, 'k')
ax.set_xlabel('Petal length')
ax.set_ylabel('Petal width')
ax.legend(loc=2)
fig.tight_layout()

逻辑回归又称为线性分类器。
什么是逻辑回归(Logistic Regression)?Logistic 模型中,每个自变量的系数有意义吗?怎么样衡量自变量的解释度?
Logistic 回归是要解可能发生事件的概率这样的问题。例如 x 是今天的温度、湿度,y 是下雨的概率。
因为 Logistic 回归是对线性组合做了映射,所以对自变量系数的解释就不像线性回归那么简单明了。
看 summary 的 P 值,P 值很小,即表明该自变量影响大。
时间序列预测
时间序列预测是个特别的线性回归问题,方程左边是未来,方程右边是过去,把历史数据作为 x,把未来作为 y。
df = pd.read_csv("Data/temperature_outdoor_2014.tsv", header=None, delimiter="\t", names=["time", "temp"])
df.time = pd.to_datetime(df.time, unit="s")
df = df.set_index("time").resample("H").mean() # 每一行是每一小时的平均温度
df_march = df[df.index.month == 3]
df_april = df[df.index.month == 4]
df_march.plot(figsize=(12, 4));
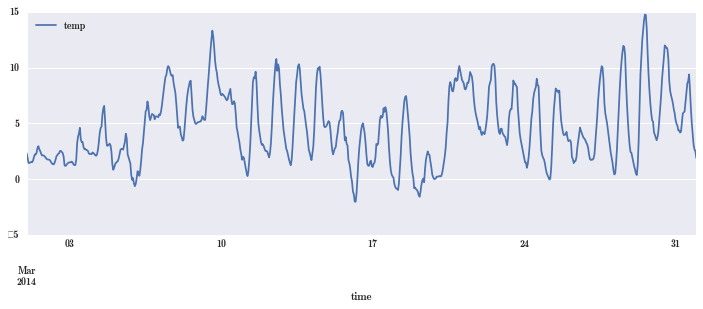
可见温度数据还是有明显的规律,有规律才可以建模型。规律体现在什么地方,画散点图研究下。
plt.scatter(df_april[1:], df_april[:-1]); # 上一小时温度和这一小时温度

滞后项的相关性称为自相关,自己的历史数据会影响后来的数据,这种规律称为自相关。
plt.scatter(df_april[2:], df_april[:-2]); # 滞后两项
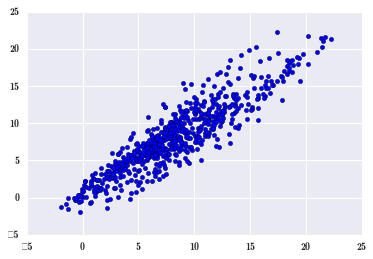
自相关有所减弱。
plt.scatter(df_april[24:], df_april[:-24]); # 昨天和今天相应时间温度
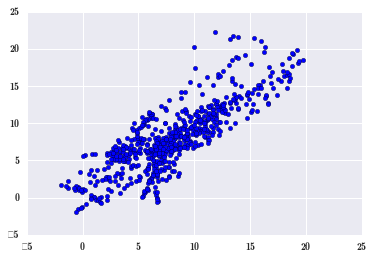
自相关,越近的数据影响越大。可以画很多相关图,相关系数图。建模时要把这种自相关性去掉,使用差分来去掉,第二张图就使用了差分,可以看到差分之后,自相关性会有所减弱,第三张图是差分的差分,第四张图是三阶差分,可以看到,差分阶次越高,自相关性就越小。
fig, axes = plt.subplots(1, 4, figsize=(12, 3))
smg.tsa.plot_acf(df_march.temp, lags=72, ax=axes[0]) # 时间序列子模块,自相关,今天的温度跟历史 72 个小时的相关性
smg.tsa.plot_acf(df_march.temp.diff().dropna(), lags=72, ax=axes[1]) # 每个条状是个相关系数
smg.tsa.plot_acf(df_march.temp.diff().diff().dropna(), lags=72, ax=axes[2])
smg.tsa.plot_acf(df_march.temp.diff().diff().diff().dropna(), lags=72, ax=axes[3])
fig.tight_layout()
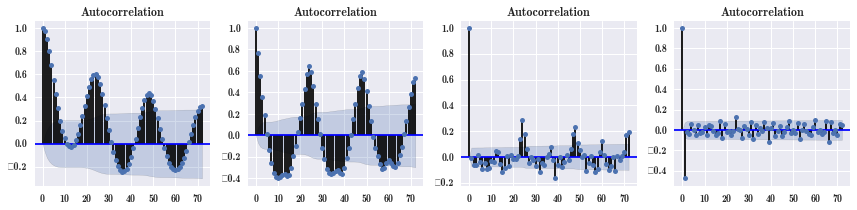
sm.tsa.AR 模型是自回归模型,从图中可以看到历史数据和现在数据会自相关,再一个,差分之后,自相关减少了,肯定可以用 AR 模型。如果图形跟上面的不一样,就可能不能使用 AR,就比较复杂了,具体可查阅时间序列相关资料。
model = sm.tsa.AR(df_march.temp) # AR 模型就是自回归模型
result = model.fit(72) #认为过去 72 小时都会影响现在时间点的温度
sm.stats.durbin_watson(result.resid) # 把残差拿出来检验下
1.998562300635305
残差是不应该有自回归的,把残差拿出来检验下,在 2 附近,意味着没有自回归。
fig, ax = plt.subplots(1, 1, figsize=(8, 3))
smg.tsa.plot_acf(result.resid, lags=72, ax=ax) # 画残差自相关性图
fig.tight_layout()
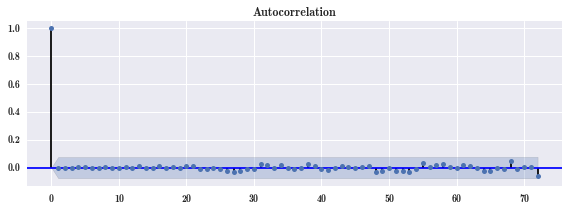
可以看出残差是没有自相关性的。
下面做预测,预测 4 月份数据。
fig, ax = plt.subplots(1, 1, figsize=(12, 4))
ax.plot(df_march.index.values[-72:], df_march.temp.values[-72:], label="train data")
ax.plot(df_april.index.values[:72], df_april.temp.values[:72], label="actual outcome")
ax.plot(pd.date_range("2014-04-01", "2014-04-4", freq="H").values,
result.predict("2014-04-01", "2014-04-4"), label="predicted outcome")
ax.legend()
fig.tight_layout()
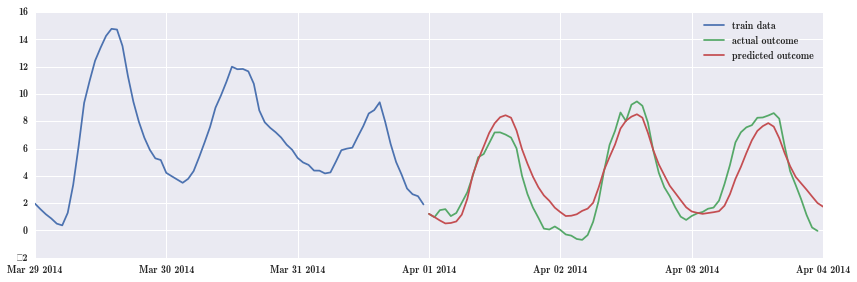
绿色是 4 月份真实值,红色是预测值,可以看到预测还是比较准确的。
什么是自相关?时间序列做差分运算会有什么样的效果?
滞后项的相关性称为自相关,自己的历史数据会影响后来的数据,这种规律称为自相关。
差分之后,自相关性会有所减弱,差分阶次越高,自相关性就越小。
补充阅读
- statsmodels 官网
- Scipy Lectures
- Numerical Python 第 14 章
- Think Stats 10-12 章



