概率与统计分析学习笔记

注：该文是上了开智学堂数据科学基础班的课后做的笔记，主讲人是肖凯老师。

概率与统计分析

描述性分析

用一个数字描述一组数字的特征。用一个数字来归纳一组数字，这个数字称为统计量或统计指标。

均值、中位数：描述一组数据的集中趋势
方差、标准差、四分位距：描述一组数据的离散趋势
相关系数：上面两大类指标都是对一个变量或一组数据的特征描述，如果要描述两个变量或两组数据的相关性，可以使用相关系数

from scipy import stats
from scipy import optimize
import numpy as np
import random
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns # 用于可视化

sns.set(style="whitegrid")

x = np.array([3.5, 1.1, 3.2, 2.8, 6.7, 4.4, 0.9, 2.2]) # 新建一个向量
print np.mean(x) # 均值
print np.median(x) # 中位数
print x.min(), x.max() # 最小最大值
print x.var() # 方差
print x.std() # 标准差
print x.var(ddof=1) # 样本方差
print x.std(ddof=1) # 样本标准差

3.1
3.0
0.9 6.7
3.07
1.75214154679
3.50857142857
1.87311810321

random.seed(123456789) # 种子不同，产生的随机数序列也不同

random.random() # 生成 0 到 1 之间的随机数，random 是随机数模块

0.6414006161858726

random.randint(0, 10)  # 生成 0 到 10 之间的一个整数

np.random.seed(123456789)

np.random.rand() # 生成 0 到 1 之间的数

0.532833024789759

np.random.randn() # 服从 0，1 的标准正态分布

0.8768342101492541

np.random.rand(5) # 同时生成 5 个从 0 到 1 均匀分布的随机数

array([ 0.71356403,  0.25699895,  0.75269361,  0.88387918,  0.15489908])

np.random.randn(2, 4) # 生成 2 行 4 列从标准正态分布产生的数

array([[ 3.13325952,  1.15727052,  1.37591514,  0.94302846],
       [ 0.8478706 ,  0.52969142, -0.56940469,  0.83180456]])

np.random.randint(10, size=10) # 生成从 0 到 9 的整数，生成 10 个

array([0, 3, 8, 3, 9, 0, 6, 9, 2, 7])

np.random.randint(low=10, high=20, size=(2, 10)) # 生成从 10 到 19 的整数，2 行 10 列

array([[12, 18, 18, 17, 14, 12, 14, 10, 16, 19],
       [15, 13, 15, 18, 11, 17, 17, 10, 13, 17]])

fig, axes = plt.subplots(1, 3, figsize=(12, 3))

axes[0].hist(np.random.rand(10000)) # 从 0 到 1 均匀分布
axes[0].set_title("rand")
axes[1].hist(np.random.randn(10000)) # 标准正态分布
axes[1].set_title("randn")
axes[2].hist(np.random.randint(low=1, high=10, size=10000), bins=9, align='left') # 从 1 到 9 的整数的均匀分布
axes[2].set_title("randint(low=1, high=10)")

fig.tight_layout()

除了从已知分布中抽取随机数，还可以使用 choice 做一些有放回或无放回的抽样。

np.random.choice(10, 5, replace=False) # 从 0 到 9 之间抽 5 个，无放回。即做抽样。replace = False 表示无放回抽样

array([9, 0, 5, 8, 1])

上面介绍的随机数种子都是全局种子，还有一种局部种子，如下例所示。

prng = np.random.RandomState(123456789) # 定义局部种子
prng.rand(2, 4)

array([[ 0.53283302,  0.5341366 ,  0.50955304,  0.71356403],
       [ 0.25699895,  0.75269361,  0.88387918,  0.15489908]])

prng.chisquare(1, size=(2, 2)) # 卡方分布

array([[  1.00418922e+00,   1.26859720e+00],
       [  2.02731988e+00,   2.52605129e-05]])

prng.standard_t(1, size=(2, 3)) # t 分布

array([[ 0.59734384, -1.27669959,  0.09724793],
       [ 0.22451466,  0.39697518, -0.19469463]])

prng.f(5, 2, size=(2, 4)) # F 分布

array([[  0.77372119,   0.1213796 ,   1.64779052,   1.21399831],
       [  0.45471421,  17.64891848,   1.48620557,   2.55433261]])

prng.binomial(10, 0.5, size=10) # 二项分布

array([8, 3, 4, 2, 4, 5, 4, 4, 7, 5])

prng.poisson(5, size=10) # 泊松分布

array([7, 1, 3, 4, 6, 4, 9, 7, 3, 6])

思考如何生成 100 个服从同一概率分布的随机数？

如果是要从标准分布中生成随机数，如 random.random 可生成 0 到 1 之间的服从均匀分布的随机数，random.randint(0, 10) 可生成 0 到 10 的均匀分布的整数，np.random.randn() 可生成服从标准正态分布的随机数。

如果要从非标准分布中生成随机数，在建模时，这种情况经常遇到，譬如研究者能提出一个新的噪声过程或现有分布的组合。用计算方法来解决复杂采样问题，一般要依赖现有的简单分布采样方法。

离散变量的逆转换采样
连续变量的逆转换采样
拒绝采样

具体可参考Computational Statistics with Matlab。

概率分布

一个随机变量可以通过某个分布函数来描述特征。

连续分布：

正态分布、均匀分布
概率分布函数 Probability distribution function

离散分布：

泊松分布、离散均匀分布
概率质量函数 Probability mass function

np.random.seed(123456789) # 定义个种子

X = stats.norm(1, 0.5) # 定义一个正态分布，期望是 1，标准差是 0.5
print type(X) # 可以看出 X 其实是个分布
print X.mean() # 期望
print X.median() # 中位数
print X.std() # 标准差
print X.var() # 方差
print [X.moment(n) for n in range(5)] # 计算各阶中心矩，下面会详细介绍
print X.stats() # 打印统计量
print X.pdf([0, 1, 2]) # 概率密度函数 pdf，给定 x 值，给出密度函数的 y 值
print X.cdf([0, 1, 2]) # 累积概率函数，其实是 pdf 积分，也就是密度曲线下的面积，整个的面积为 1
X.rvs(10) # 用于生成随机数，跟前面 random 模块功能类似
X.interval(0.95) # 整个函数比较有用，计算曲线下面积为 0.95 时对应的两个 x 值

<class 'scipy.stats._distn_infrastructure.rv_frozen'>
1.0
1.0
0.5
0.25
[1.0, 1.0, 1.25, 1.75, 2.6875]
(array(1.0), array(0.25))
[ 0.10798193  0.79788456  0.10798193]
[ 0.02275013  0.5         0.97724987]





(0.020018007729972975, 1.979981992270027)

穿插个知识点：上面的 moment 函数是计算随机变量的各阶中心矩，这里简单介绍下统计中矩的概念。

定义设 X 为随机变量，c 为常数，k 为正整数。则量\(E[(X-c)^k]\)称为 X 关于 c 点的 k 阶矩。

有两种比较重要的情况：

当 \(c=0\) 时，\(\alpha_{k}=E(X^k)\)称为 X 的 k 阶原点矩；

当 \(c=E(X)\) 时，\(\mu_{k}=E[(X-EX)^k]\) 称为 X 的 k 阶中心矩。

一阶原点矩就是期望，一阶中心矩为 0，二阶中心矩就是 X 的方差。在统计学上，高于四阶的极少使用，三、四阶有些应用，但也不多。

矩的应用之一是用三阶中心距 \(\mu_{3}\) 去衡量分布是否有偏。设 X 的概率密度函数为 f(x)，若 f(x) 关于某点 a 对称，即

\[f(a+x)=f(a-x) \]

则 a 必等于 \(E(X)\)，且 \(\mu_{3}=E[X-E(X)]^{3}=0\)。如果\(\mu_{3}>0\)，则称分布为正偏或右偏。如果\(\mu_{3}<0\)，则称分布为负偏或左偏。特别地，对正态分布而言有 \(\mu_{3}=0\)，故如 \(\mu_{3}\) 显著异于 0，则是分布与正态有较大偏离的标志。由于 \(\mu_{3}\) 的因次是 X 的因次的三次方，为抵消这一点，以 X 的标准差的三次方，即 \(\mu_{2}^{3/2}\)去除 \(\mu_{3}\)，其商

\[\beta_{1}=\frac{\mu_{3}}{\mu_{2}^{3/2}} \]

称为 X 或其分布的“偏度系数”。

def plot_rv_distribution(X, axes=None):
    """Plot the PDF, CDF, SF and PPF of a given random variable"""
    if axes is None:
        fig, axes = plt.subplots(1, 2, figsize=(8, 3))
    
    x_min_999, x_max_999 = X.interval(0.999)
    x999 = np.linspace(x_min_999, x_max_999, 1000)

    x_min_95, x_max_95 = X.interval(0.95)
    x95 = np.linspace(x_min_95, x_max_95, 1000)

    if hasattr(X.dist, 'pdf'): # 判断有没有 pdf，即是不是连续分布
        axes[0].plot(x999, X.pdf(x999), label="PDF")
        axes[0].fill_between(x95, X.pdf(x95), alpha=0.25) # alpha 是透明度，alpha=0 表示 100% 透明，alpha=100 表示完全不透明
    else: # 离散分布
        x999_int = np.unique(x999.astype(int))
        axes[0].bar(x999_int, X.pmf(x999_int), label="PMF") # pmf 和 pdf 是类似的
    axes[1].plot(x999, X.cdf(x999), label="CDF")
    
    for ax in axes:
        ax.legend()
    
    return axes

fig, axes = plt.subplots(3, 2, figsize=(12, 9)) # 画布，3 行 3 列

X = stats.norm() # 标准正态分布
plot_rv_distribution(X, axes=axes[0, :])
axes[0, 0].set_ylabel("Normal dist.")
X = stats.f(2, 50) # F 分布
plot_rv_distribution(X, axes=axes[1, :])
axes[1, 0].set_ylabel("F dist.")
X = stats.poisson(5) # 泊松分布
plot_rv_distribution(X, axes=axes[2, :])
axes[2, 0].set_ylabel("Poisson dist.")

fig.tight_layout()

概率密度函数（Probability density function）和累积概率分布函数（Cumulative distribution function）分别是什么？它们之间有什么样的关系？

定义设 X 为一随机变量，则函数

\[P(X\le x)=F(x) (-\infty<x<\infty) \]

称为 X 的分布函数。这里并未限定 X 为离散型的，它对任何随机变量都有定义。

定义设连续性随机变量 X 有概率分布函数 F(x)，则 F(x) 的导数 \(f(x)=F'(x)\) 称为 X 的概率密度函数。

CDF 是 PDF 的积分，也就是 PDF 曲线下的面积。

离散概率分布与连续概率分布的累积分布曲线看起来有什么不同？

离散概率分布的累积分布曲线是阶梯状的，连续概率分布的累积分布函数是平滑的。如上图右边的三幅图都是累积分布曲线，上两幅是连续概率分布的累积分布函数，最下面一幅是离散概率分布的累积分布曲线。

假设检验

假设检验在统计学里占有非常重要的地位，步骤如下：

构造原假设和备择假设
选择某个检验统计量，例如 T 检验统计量
收集数据
根据数据计算统计量和相应的 P 值
若 P 值很小，拒绝原假设

np.random.seed(123456789)
mu, sigma = 1.0, 0.5 # 均值，标准差
X = stats.norm(mu-0.2, sigma) # 均值为 0.8，标准差为 0.5
n = 100 
X_samples = X.rvs(n) # 生成 100 个随机数
plt.hist(X_samples);

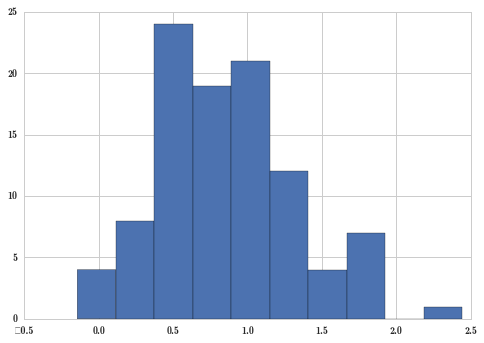
上面的采样数据真正的参数是，均值 0.8，标准差 0.5。我们假装不知道这些数据是由均值 0.8、标准差 0.5 的正态分布定义的，假装只知道这 100 个数字，那么我们的问题是，它们的分布参数的均值是不是 1 呢？

如果样本真的是由 mu=1 的分布产生的，那么样本的均值应该离 mu 不太远。而样本的均值是可以通过 mean 函数计算出来的。

X_samples.mean() # 求样本的均值

0.85830510224950851

样本均值 0.85 离 1 不太远，有可能样本就是从均值为 1 的分布出来的。如果样本均值是 0 或者 10，那么离 1 就太远了，我们肯定就怀疑这样本不是从均值为 1 的分布产生的。

首先定义样本均值和总体均值的距离。

z = (X_samples.mean() - mu)/(sigma/np.sqrt(n)) # 样本均值和总体参数均值的距离
print z

-2.83389795501

z 表示样本均值和总体均值的距离。z 越大，表示样本均值距离总体均值越大，那么就越要怀疑原假设，原假设即样本是由均值为 mu 的分布产生的。z 越小，表示距离越近，则可以同意原假设，或者说不反对原假设。

那 z 多大算大，多小算小呢？这就需要一个临界值，我们是通过抽样分布的特点来判断临界值的。

这里 z 是服从标准正态分布的，所以下面可以方便计算 z 的概率。

在具体计算距离时，有两种情况，一种是知道总体标准差的，如上式；另一种情况是不知道总体标准差，要用样本标准差来代替，如下式。

t = (X_samples.mean() - mu)/(X_samples.std(ddof=1)/np.sqrt(n))
print t

-2.96803385457

stats.norm().ppf(0.025)

-1.9599639845400545

2 * stats.norm().cdf(-abs(z))

0.0045984013290753566

2 * stats.t(df=(n-1)).cdf(-abs(t))

0.0037586479674227209

以上是整个计算过程细节，如果你不需要了解这些细节，那可以直接用 stats 模块中的单变量 T 检验 ttest_lsamp 来做这个事情。

t, p = stats.ttest_1samp(X_samples, mu) # 传入证据及参数，数据即证据，注意这里并没有传入标准差 sigma，对于 T 检验，标准差是未知的
print t
print p

-2.96803385457
0.00375864796742

p 值小于 0.05，可以拒绝原假设，即认为数据不是从总体均值为 mu 的分布产生的。

fig, ax = plt.subplots(figsize=(8, 3))

sns.distplot(X_samples, ax=ax) # 画真实数据的图形，蓝色线，分布其实是以 0.8 为期望值
x = np.linspace(*X.interval(0.999), num=100)
ax.plot(x, stats.norm(loc=mu, scale=sigma).pdf(x)) # 理论上值 mu=1

fig.tight_layout()

以上分析是单样本假设检验，还有多样本假设检验，如两样本，我们要看两样本是不是来自同一分布。

mu1, mu2 = np.random.rand(2) # 随机产生两个不同的参数
print mu1,mu2
X1 = stats.norm(mu1, sigma) # 标准差一样
X1_sample = X1.rvs(n) # 生成第 1 组数据
X2 = stats.norm(mu2, sigma)
X2_sample = X2.rvs(n) # 生成第 2 组数据
t, p = stats.ttest_ind(X1_sample, X2_sample) # 两样本 T 检验
print t
print p # p 值太小，可以拒绝原假设

0.329631563852 0.692241009083
-5.48067917083
1.2796633829e-07

sns.distplot(X1_sample);
sns.distplot(X2_sample);

两样本 T 检验可用于判断两个生产线上的产品是否有显著区别等。

如何理解零假设跟备择假设？

零假设是一个在做实验之前原有的假设，备择假设是指，一旦你决定否定原假设，则这假设可备你选择。

假设检验就是，根据观察或实验结果去检验零假设是否成立。

接受零假设意味着，从所获数据来看，并无足够的根据认为零假设不对，而不是说，从所获数据证明了零假设是对的，因此，问题多少仍处于未决的局面。反之，否定原假设则意味着，按所获数据有充足的理由认为零假设不对，即有充足的理由认为对立假设成立，故在一定限度内，可以说问题有了一个明确的结论。

如何理解 p 值，p 值代表了什么事件的概率？

p 值就是数据对原假设的支持程度。

p 值大于 0.05 时，应该拒绝备择假设吗？

p 值表达了实验结果对零假设的支持程度，指定一个界限，若 p 小于所指定的界限，则决定不接受原假设，不然就接受原假设。这个界限最常用的是 0.05，其次是 0.01，0.1 等等。

p 值大于 0.05 时，要不要拒绝备择假设，还是要看具体情况，不是所有的情况都非得把界限定为 0.05，或更小的 0.01。

当界限是 0.05 时，若 p 值大于 0.05，只能说明，并无足够的理由认为零假设不对，而不是说备择假设就是错的，所以其实问题仍是未决的局面，还有待做更多的研究。

p 的具体值也很重要，如果 p=0.051，则尽管大于 0.05，但已很接近界限，因此可以说，虽然试验结果仍维持了原假设，但已很不利于它，这时拒绝备择假设会犹豫不决；如果 p=0.85，则可以说试验结果不仅维持了原假设，还很有利于它，这时候拒绝备择假设就没什么疑问了。

一类错误和二类错误

在检验一个假设时，可能搞对了（原假设成立而接受它，或者原假设不对而否定它），也可能犯以下两类错误之一：

原假设成立，但被否定了，这称为第一类错误。
原假设不对，但被接受了，这称为第二类错误。

是否犯错误，取决于所用的检验方法及所获得的样本即试验数据。而犯哪一类错误，则取决于原假设是否成立，若原假设成立，则不会犯第二类错误；若原假设不成立，则不会犯第一类错误。

这么说不难理解，但难以把这两类错误联系起来，下面举个很不严谨的例子来体会下。

我们经常说，法律不会冤枉一个好人，但也不会放过一个坏人。这里的冤枉好人，就是第一类错误。放过坏人，即不是好人，但被误认为是好人，就是第二类错误。

在对嫌疑人一无所知时，应假定人是好人，即零假设是，人是好人。

「不冤枉好人」和「不放过坏人」之间有没有冲突呢？

有。比如，假设某年某地出了个大冤案，一个好人被冤枉住了二十年牢才被发现是冤案，震惊全国，于是当年全国很多地方在判案时就更加严格，没有十足的把握，没有实打实的证据，就认为嫌疑人是好人放走，这样大大减少了冤枉好人的概率，但同时也增加了放走坏人的概率，好多坏人因为证据不足而释放。再比如，某些年份犯罪横行，于是当局在全国组织了严厉打击犯罪的行为，只要有犯罪证据就抓起来，最终确实处理了一批坏人，但也有不少好人被冤枉。

可见，要想「不冤枉一个好人」，就很有可能放过不少坏人，要想「不放过一个坏人」，就很有可能冤枉不少好人。就看需要证据的多少，也就是个界限，需要多少证据才能断定嫌疑人不是好人，在假设检验中也就是检验水平 \(\alpha\)。

这里好多人会有困惑，干嘛非得在两种错误「冤枉好人」和「放过坏人」之间游移，难道就不能全部正确断案？

很难。虽然嫌疑人有没有干坏事是确定无疑的，但我们并不知道这个事实，我们只有看证据，看能搜集到多少证据，看证据的力度。在假设检验里，就是看数据，你说零假设是对的，但在零假设的情况下，这数据就基本不会出现，现在出现了，你说零假设是正确的，谁信？这里的数据是采样数据，不是总体，所以才需要假设检验。如果有全部证据，那判案就没什么难的了。

要想保证判案正确率，就要搜集更多证据，要花更多时间和精力。假设检验只是在现有数据的情况下，给出的检验结果。可见，统计方法虽是一种有力的科学方法，但无法搞无米之炊。

非参数推断

对一组数据，我们希望用一个分布来描述它的特征，比如正态分布，可以用一个公式来描述数据，但公式要能够跟数据拟合，才能做参数推断。但现实情况下，数据不能跟公式很好地拟合，这就需要让数据自己说话，这就是非参数推断。

np.random.seed(0) # 先定义个种子
X = stats.chi2(df=5) # 卡方分布
X_samples = X.rvs(100) # 用卡方分布生成 100 个随机数
print X_samples

[ 11.87740141   5.62133928  12.48424465   2.04604944   4.03651267
   5.65798023   6.98206807   4.70149541   5.77577501   5.39173922
  10.38780279   3.75698915   0.32533609   6.55639806  15.03828046
   1.30710924  10.5932091   10.25799631   2.20999289   0.72662779
   9.05799941   8.92433257   1.9214374    1.35311843   2.9994597
   3.16738619   1.10704806   3.73673066   2.19559054   5.57505371
   4.25089547   5.72057502   2.72133868   3.35077109   2.35324329
   0.97911165   1.08783953   5.84349338   6.85360346   4.72424779
   5.62899185   2.61378879   3.47933568   4.50079157   1.72867406
   7.56307388   5.85384885   1.20166469   8.81234066   3.8249378
   3.25148226   9.02029235   5.46938978   6.76401061   4.71779307
   5.62775727   1.56601507   7.85948981   3.2261648    2.48433029
  12.48425043   7.58536446   3.59126794   7.1509955    6.40418286
   7.65468192   5.53864837   1.83570203   5.27195502   9.52840427
   3.17436839  12.37551801   2.4389755    6.12259088   2.71804987
   6.64531598   5.60681827   1.84624872   4.84275986   6.48454567
   2.16327754   8.52369442   4.13552411  11.58741286   4.04991086
   2.65887737   1.75703528   3.1679936    3.02630659  12.8572994
   1.63427047   7.32466393   2.00537696   1.19102088   7.64888505
   5.34099642   1.94603823   6.66554219   2.37237427   2.60384033]

假设我们不知道这些数是通过卡方分布产生的，现在要推断分布的形状，只能采取一些经验的方法，其中一种方法是核分布。

kde = stats.kde.gaussian_kde(X_samples) # 高斯核函数，kde 是核函数密度估计，核分布是种非参数估计方法
kde_low_bw = stats.kde.gaussian_kde(X_samples, bw_method=0.25) # bw_method 为窗宽参数，该值越小，就越受到数据本身的影响
x = np.linspace(0, 20, 100)

fig, axes = plt.subplots(1, 3, figsize=(12, 3))

axes[0].hist(X_samples, normed=True, alpha=0.5, bins=25)
axes[1].plot(x, kde(x), label="KDE")
axes[1].plot(x, kde_low_bw(x), label="KDE (low bw)")
axes[1].plot(x, X.pdf(x), label="True PDF")
axes[1].legend()
sns.distplot(X_samples, bins=25, ax=axes[2])

fig.tight_layout()

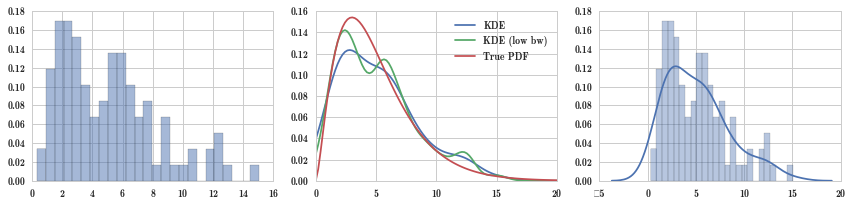
可以看到，理论分布 True PDF 是非常平滑的，因为是公式定义出来的，而核密度估计 KDE 是直接由数据拟合出来的，所以又称为经验分布。bw_method 是窗宽参数，该值越小，核密度估计就越受到数据的影响，上面的数据是有双峰的，kde_low_bw 确实受数据影响比较厉害。

参数方法和非参数方法都是用来估计给定数据的分布，都是要从实际数据推断背后分布的样子，区别在于，参数方法背后是由数学公式定义的，而非参数方法则没有。

用非参数方法估计出数据背后的经验分布后，可以使用该经验分布来进一步抽样。

kde.resample(10) # 使用非参数估计的经验分布来进一步抽样

array([[ 1.75376869,  0.5812183 ,  8.19080268,  1.38539326,  7.56980335,
         1.16144715,  3.07747215,  5.69498716,  1.25685068,  9.55169736]])

这里经验分布 KDE 没有累积分布函数，我们可以手工计算。

def _kde_cdf(x):
    return kde.integrate_box_1d(-np.inf, x) # 得到经验分布的累积分布图形

kde_cdf = np.vectorize(_kde_cdf) # 向量化函数

fig, ax = plt.subplots(1, 1, figsize=(8, 3))

sns.distplot(X_samples, bins=25, ax=ax)
x = np.linspace(0, 20, 100)
ax.plot(x, kde_cdf(x))

fig.tight_layout()

思考何种情况下使用非参数推断？

你用过 Python 的内置函数 map 吗？Numpy 里面有类似的方法吗？

map 可以把一个函数作用到向量的每个元素，np.vectorize 也可实现这种功能，把函数向量化，函数就可以处理向量了。

补充阅读

参考资料

posted @ 2016-06-07 23:19 疯狂的拖鞋阅读(6516) 评论(0) 编辑收藏举报

刷新页面返回顶部

代冕