机器学习笔记—再谈广义线性模型
前文从线性回归和 Logistic 回归引出广义线性回归的概念,很多人还是很困惑,不知道为什么突然来个广义线性回归,有什么用?只要知道连续值预测就用线性回归、离散值预测就用 Logistic 回归不就行了?还有一些概念之间的关系也没理清,例如线性回归和高斯分布、Logistic 回归和伯努利分布、连接函数和响应函数。
这种困惑是可以理解的,前文为了引导快速入门,从实战解题的角度推出了答案,但对其背后的概率假设解释不足,虽然线性回归专门开辟一节来介绍高斯分布假设,但很多人误以为这一节的目的只是为了证明最小均方误差的合理性,Logistic 回归的伯努利分布假设也需做解释。
线性回归是建立在高斯分布的假设上,Logistic 回归是建立在伯努利分布的假设上。如果不能从概率的角度理解线性回归和 Logistic 回归,就不能升一级去理解广义线性回归,而广义线性模型就是要将其它的分布也包纳进来,提取这些分布模型的共同点,成为一个模型,这样再遇到其它分布,如多项式分布、泊松分布、伽马分布、指数分布、贝塔分布和 Dirichlet 分布等,就可以按部就班地套模型进行计算了。
有些同学不明白的是,「当给定参数 θ 和 x 时,目标值 y 也服从正态分布」,这里 y 服从的是均值为 θTx 的正态分布,当我们训练得到参数 θ 后,那么对于不同的 x 值,y 服从的就是不同均值的正态分布。伯努利分布也一样。
要想掌握广义线性模型,得亲自动手做一个实例。
下面我们从概率的角度重新审视线性回归、Logistic 回归,来加深对广义线性模型的理解。
先说线性回归,假设是 y(i)|x(i);θ~N(θTx(i),σ2),因为 σ2 对 θ 值和 hθ(x) 值没有影响,所以我们不妨设 σ2=1,那么

把该高斯分布写成指数分布簇的形式:


可得:

根据广义线性模型的假设,得:

其中 hθ(x)=η 就是响应函数,其反函数就是连接函数。
如果我们有 m 个例子的训练集 {(x(i),y(i));i=1,...,m},想要学习这个模型的参数 θ,log 似然函数为:
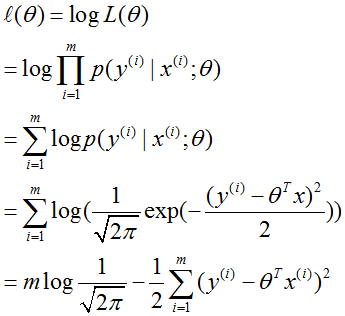
然后最大化该函数即可得解。
再来看 Logistic 回归,假设是给定 x 和 θ 后的 y 服从伯努利分布。
p(y;Φ)=Φy(1-Φ)1-y
把该伯努利分布写成指数分布簇的形式:
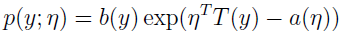

可得:
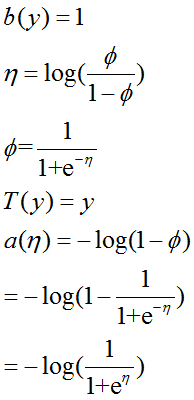
根据广义线性模型的假设,得:

其中 hθ(x)=1/(1+e-η) 就是响应函数,其反函数就是连接函数。
如果我们有 m 个例子的训练集 {(x(i),y(i));i=1,...,m},想要学习这个模型的参数 θ,log 似然函数为:
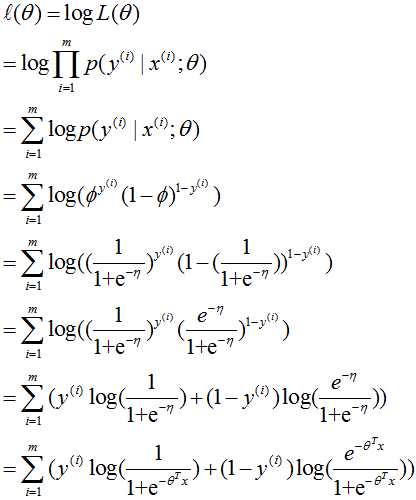
然后同样最大化该函数即可得解。
由此,大致可得使用广义线性模型的步骤:
1、分析数据集,确定概率分布类型;
2、把概率写成指数分布簇的形式,并找到对应的 T(y)、η、E(y;x) 等。
3、写出 log 最大似然函数,不同的分布所使用的连接函数不一样,并找到使该似然函数最大化的参数值。
参考资料:
1、http://cs229.stanford.edu/notes/cs229-notes1.pdf



