[测试题]数组(array)

Description

Input

Output

Sample Input1

3 2 7
5 4 2

Sample Output1

999999732

Sample Explanation1

Sample Input2

5 3 1
5 4 3 5 5

Sample Output2

0

Sample Explanation2

Hint

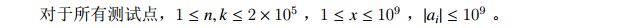
题解

由于负数是肯定小于正数的，我们首先想到的就是将乘积变成负数。我们可以统计输入的负数个数。

那么会有两种情况：

$(i)$无论怎么变变不了负数，这个时候我们将所有数取绝对值。

我们需要使乘积最小，这时只需要将绝对值最小的数减小即可。

证明：

假设有四个正整数$a_1,a_2,a_3,a_4$，满足$a_1<a_2<a_3<a_4$。需要减去$x$。

我们取极端情况若$a_1-x$：

原式$=(a_1-x)*a_2*a_3*a_4$

　　$=a_1*a_2*a_3*a_4-x*a_2*a_3*a_4$

若$a_4-x$：

原式$=a_1*a_2*a_3*(a_4-x)$

　　$=a_1*a_2*a_3*a_4-x*a_1*a_2*a_3$

由于$-x*a_2*a_3*a_4<-x*a_1*a_2*a_3$

显然得证。

$(ii)$可以变成负数，我们变完负数后同样将所有数取绝对值。

既然已经是负数了，那我们只需所有的数的绝对值积最大即可。

证明同上，只是改变了加减。

所以我们只需要用小根堆维护绝对值最小的数即可。

我是用两个堆分别维护正数和负数。同时注意不要边减边取模，因为保存的是绝对值，和负数直接取模不同。

详见代码。

  1 #include<map>
  2 #include<ctime>
  3 #include<cmath>
  4 #include<queue>
  5 #include<stack>
  6 #include<vector>
  7 #include<string>
  8 #include<cstdio>
  9 #include<cstring>
 10 #include<cstdlib>
 11 #include<iostream>
 12 #include<algorithm>
 13 #define LL long long
 14 #define RE register
 15 #define IL inline
 16 using namespace std;
 17 const LL N=2e5;
 18 const LL MOD=1e9+7;
 19 
 20 priority_queue<LL, vector<LL>, greater<LL> >a,b;
 21 LL n,k,x,ai;
 22 LL cnt;
 23 bool flag;
 24 IL void print()
 25 {
 26     LL sum=1;
 27     while (!a.empty())
 28     {
 29         LL tmp=-a.top()%MOD;a.pop();
 30         sum=(sum*tmp)%MOD;
 31     }
 32     while (!b.empty())
 33     {
 34         LL tmp=b.top()%MOD;b.pop();
 35         sum=(sum*tmp)%MOD;
 36     }
 37     printf("%lld\n",(sum+MOD)%MOD);
 38     exit(0);
 39 }
 40 IL void cuta()
 41 {
 42     if (a.top()/x+(bool)(a.top()%x)>=k)
 43     {
 44         LL tmp=a.top();a.pop();
 45         tmp=(tmp-(LL)k*(LL)x/*%MOD*/)/*%MOD*/;
 46         a.push(tmp);
 47         print();
 48     }
 49     else
 50     {
 51         LL tmp=a.top();a.pop();
 52         tmp=(tmp-(LL)(a.top()/x+(bool)(a.top()%x))*(LL)x)/*%MOD*/;
 53         k-=a.top()/x+(bool)(a.top()%x);
 54         b.push(-tmp);
 55     }
 56 }
 57 IL void cutb()
 58 {
 59     if (b.top()/x+(bool)(b.top()%x)>=k)
 60     {
 61         LL tmp=b.top();b.pop();
 62         tmp=(tmp-(LL)k*(LL)x/*%MOD*/)/*%MOD*/;
 63         b.push(tmp);
 64         print();
 65     }
 66     else
 67     {
 68         LL tmp=b.top();b.pop();
 69         tmp=(tmp-(LL)(b.top()/x+(bool)(b.top()%x))*(LL)x)/*%MOD*/;
 70         k-=b.top()/x+(bool)(b.top()%x);
 71         a.push(-tmp);
 72     }
 73 }
 74 IL LL getnum()
 75 {
 76     if (a.empty()) {flag=0;LL tmp=b.top();b.pop();return tmp;}
 77     if (b.empty()) {flag=1;LL tmp=a.top();a.pop();return tmp;}
 78     if (a.top()>b.top()) {flag=0;LL tmp=b.top();b.pop();return tmp;}
 79     {flag=1;LL tmp=a.top();a.pop();return tmp;}
 80 }
 81 
 82 int main()
 83 {
 84     scanf("%lld%lld%lld",&n,&k,&x);
 85     for (RE LL i=1;i<=n;i++)
 86     {
 87         scanf("%lld",&ai);
 88         if (ai<0) cnt++,a.push(-ai);
 89         else b.push(ai);
 90     }
 91     if (cnt%2==0)
 92     {
 93         if (cnt==0) cutb();
 94         else if (cnt==n) cuta();
 95         else
 96         {
 97             if (a.top()>=b.top()) cutb();
 98             else cuta();
 99         }
100     }
101     if (!k) print();
102     while (k--)
103     {
104         LL tmp=getnum();
105         tmp=(tmp+x)/*%MOD*/;
106         if (flag) a.push(tmp);
107         else b.push(tmp);
108     }
109     print();
110     return 0;
111 }

 

posted @ 2017-08-17 16:59  NaVi_Awson  阅读(354)  评论(0)  编辑  收藏  举报