【HDU4912】Paths on the tree

题面

bobo有一棵树，其顶点方便地用1,2...n标记。

树上有m条路径。 BOBO想挑一些路径，同时任何两个路径不共享共同的顶点。

找到bobo可以选择的最大路径数。

输入包括几个测试。 对于每个测试：

第一行包含n，m（1≤n，m≤10⁵）。 以下（n-1）行中的每一行包含2个整数a i，b i表示顶点a i和b i之间的边（1≤ai，bi≤n）。

之后m行中的每一行包含2个整数u i，v i表示顶点u i和v i之间的路径（1≤ui，vi≤n)。

对于每组数据，输出一个最大路径数。

分析

lca+贪心

贪心的决策是将所有的路径的两端点的lca求出来，按深度从大到小选择。

因为对于一组点的lca,在它下面的所有点都将不能再被访问。

比如对于下图（设1为根）

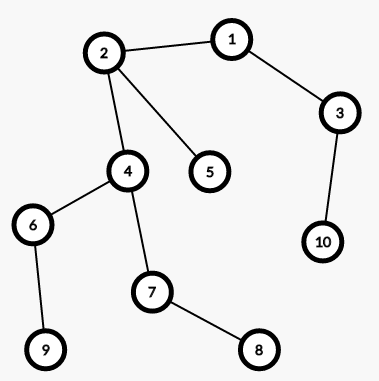
如果我们有两个选择（9,8）和（5,6）

如果这两个不冲突，当然是直接都选了，然而这里是冲突的

lca(9,8)=4,lca(5,6)=2,dep[4]=3,dep[2]=2

显然，后者的路径里经过了前者的lca，所以后者能使更多点不可被访问，而前者明显影响的点更少。

每次我们只需要dfs标记路上访问过的点，计算答案的时候询问两端点是否被访问过。

为什么只需要知道两端点呢？因为我们的贪心是满足性质lca深度较小的是优先选择的，所以后选的lca一定是比较上面的。

假如目前这个还没有被选择的路径上有一个点在已经被选择的路径上，那么后面这条路径的lca的深度肯定比前面那条大啊，因为前面那条的lca在最上方的端点,而后面这条的lca在路径中间。既然假设不成立，说明没有目前这个路径没有点在已经被选择过的路径上。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 100100
int n,m,cnt,cot,ans;
int dep[N],vis[N],first[N];
int fa[N][20];
struct email
{
    int u,v;
    int nxt;
}e[N*4];
struct wjym
{
    int u,v,l,d;
}a[N*4];

inline void add(int u,int v)
{
    e[++cnt].nxt=first[u];first[u]=cnt;
    e[cnt].u=u;e[cnt].v=v;
} 

bool cmp(wjym a,wjym b)
{
    return a.d>b.d;
}

inline void init()
{
    cnt=0;cot=0;ans=0;
    memset(vis,0,sizeof(vis));
    memset(dep,0,sizeof(dep));
    memset(fa,0,sizeof(fa));
    memset(first,0,sizeof(first));
}

inline void dfs(int u,int f)
{
    for(int i=1;(1<<i)<=dep[u];i++)
        fa[u][i]=fa[fa[u][i-1]][i-1];
    for(int i=first[u];i;i=e[i].nxt)
    {
        int v=e[i].v;
        if(v==f)continue;
        fa[v][0]=u;
        dep[v]=dep[u]+1;
        dfs(v,u);
    }
}

inline int lca(int x,int y)
{
    if(dep[x]<dep[y])
        swap(x,y);
    int t=dep[x]-dep[y];
    for(int i=0;(1<<i)<=t;i++)
        if((1<<i)&t)
            x=fa[x][i];
    if(x==y)return x;
    for(int i=19;i>=0;i--)
        if(fa[x][i]!=fa[y][i])
            x=fa[x][i],y=fa[y][i];
    return fa[x][0];
}

inline void readd(int u,int v)
{
    a[++cot].u=u;a[cot].v=v;
    a[cot].l=lca(u,v);a[cot].d=dep[a[cot].l];
} 

inline void color(int u)
{
    vis[u]=1;
    for(int i=first[u];i;i=e[i].nxt)
    {
        int v=e[i].v;
        if(dep[v]>dep[u]&&!vis[v])
            color(v);    
    }
}

int main()
{
    while(scanf("%d%d",&n,&m)==2)
    {
        init();
        for(int i=1;i<n;i++)
        {
            int u,v;
            scanf("%d%d",&u,&v);
            add(u,v);add(v,u);
        }
        dfs(1,0);
        for(int i=1;i<=m;i++)
        {
            int u,v;
            scanf("%d%d",&u,&v);
            readd(u,v);
        }
        sort(a+1,a+1+m,cmp);
        for(int i=1;i<=m;i++)
        {
            int u=a[i].u,v=a[i].v,l=a[i].l;
            if(!vis[u]&&!vis[v])
                color(l),ans++;
        }
        printf("%d\n",ans);
    }
    return 0;
}