数据结构:堆排序
数据结构:堆排序
走进堆排序
什么是堆
堆(英语:Heap)是计算机科学中的一种特别的树状数据结构。堆实质是一颗完全二叉树。它就长下面这样:
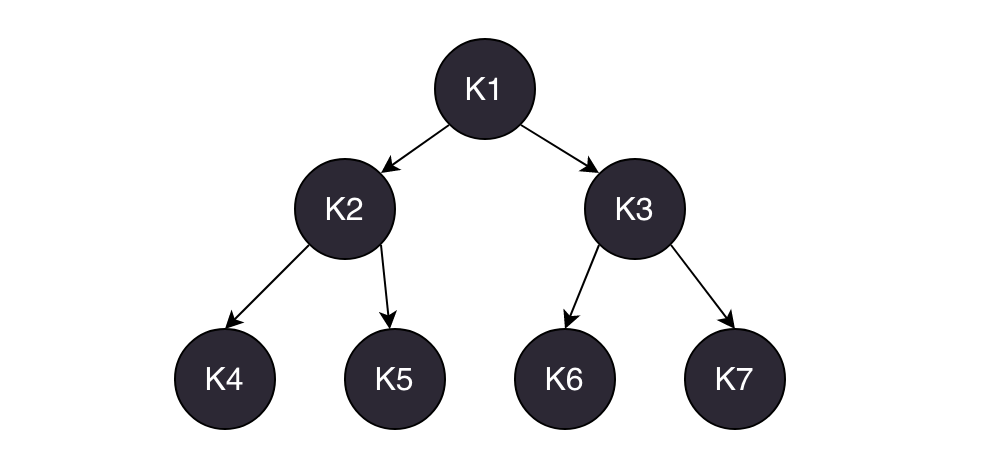
正是由于他在形式上是一个完全二叉树,我们也将其可以用数组来存储。其中Kn的子元素的下标是是K(n*2)和K(n*2+1)。
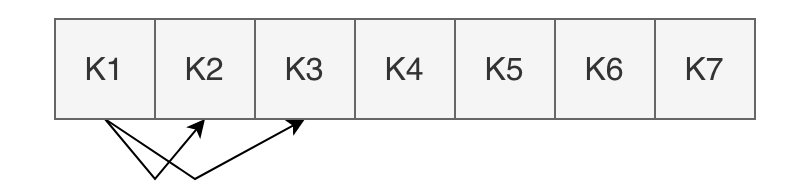
但是堆是一种特殊完全二叉树,它的元素遵循两种规律,每一个节点的值要么大于其所有子节点,要么小于其所有子节点,类似下面这样:
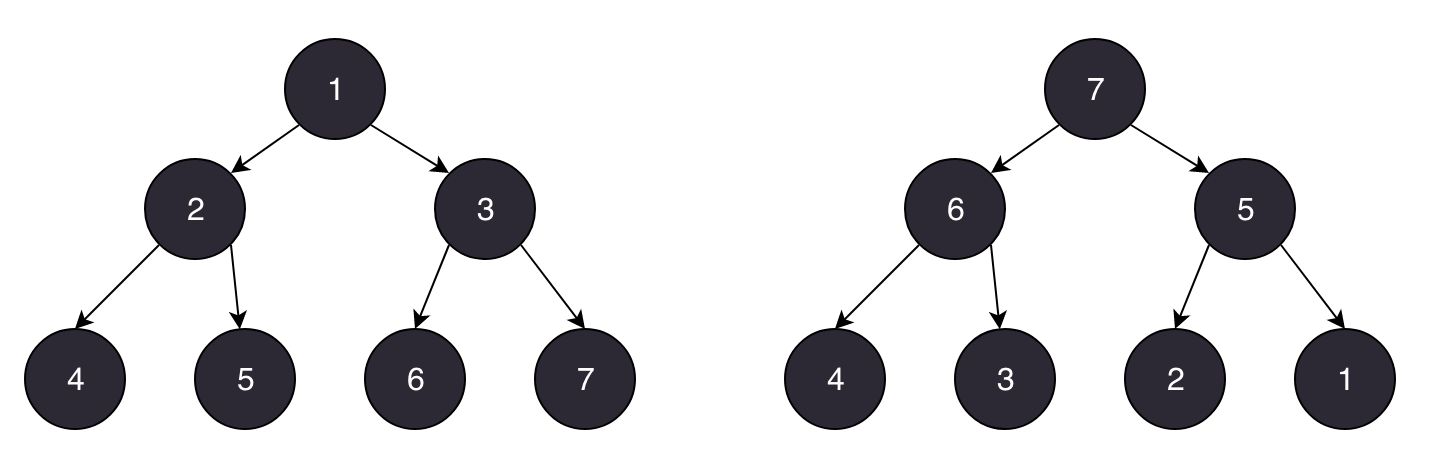
根据节点与其子节点的关系,可以分为大顶堆(右)和小顶堆(左),从中不难发现,大顶堆从上往下依次键值减小,小顶堆从上向下键值增大。其实在这里,我们就可以发现堆的一大应用,即因为其结构的特殊性,处在第一个位置上的元素一定是最大或者最小的。
什么是堆排序
☐ 对一组待排序记录的关键字,首先把它们按堆的定义建成小(大)顶堆
☐ 然后输出堆顶的最小(大)关键字所代表的记录,再对剩余的关键字建堆,以便得到次小(大)的关键字
☐ 如此反复进行,直到全部关键字排成有序序列为止。
说白了,堆排序就是不断取走堆中最大元素或者最小元素(即第一个元素),然后对剩下元素进行建堆,再重复的一个过程。
堆的两条重要性质:
1.在一个二叉堆中,位置为K的节点的父节点的位置为|_K/2_|,而它的两个子节点位置为2K和2K+1
2.一颗大小为N的完全二叉树的高度为|_LgN_|
图示堆排序
堆排序实质是对一组关键字进行建堆的过程,这一过程可称为堆的有序化。我们此处将的是大顶堆,小顶堆的道理是相同的。
插入新的元素进行有序化
如下图所示,我们的目标是大顶堆,然而新插入的元素值为9,大于其父元素,所以我们需要进行有序化:
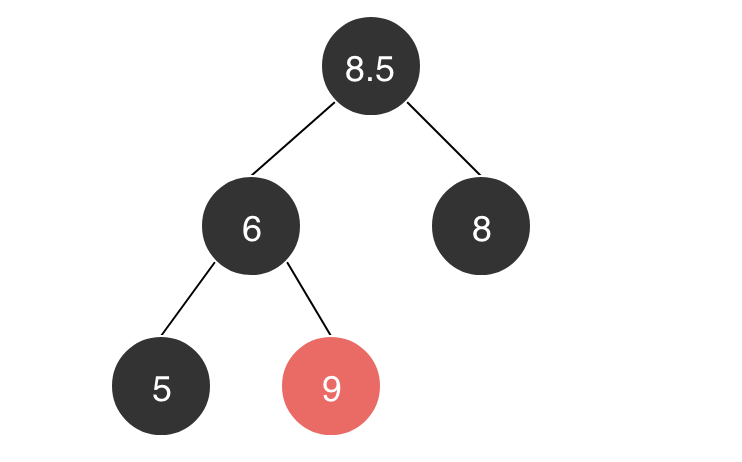
我们将子元素设为X(图中值为9),我们需要交换它和它的父节点(值为6)来修复堆。但是可能交换后X还是很大(大于值为8.5的元素),所以我们需要X一次次的它的祖先节点进行比较,直到找打它最合适的位置。根据二叉堆的性质,我们不难发现只要记住位置为K的节点的父节点为 |_K/2_|,一切都很简单了。
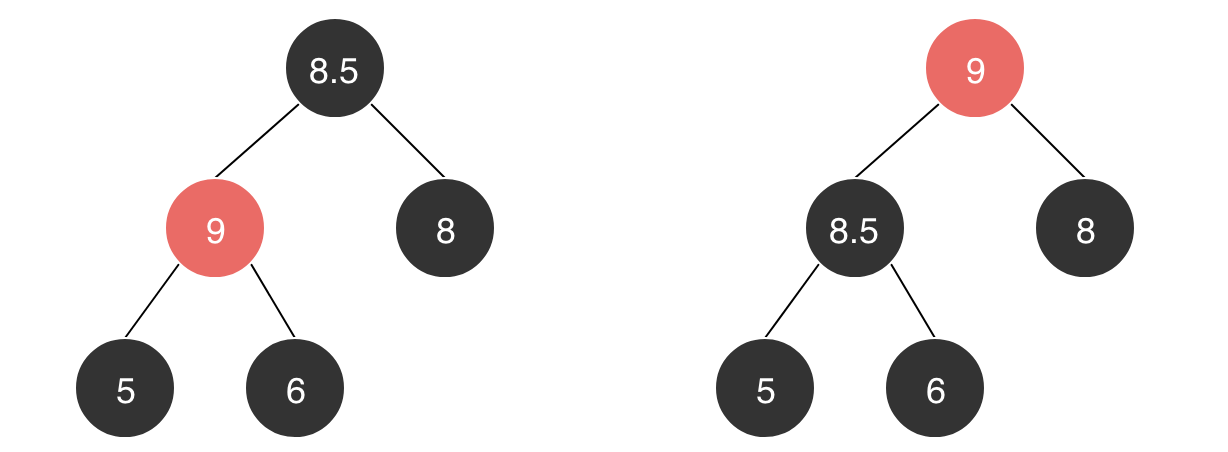
这就是一种上浮操作,即新插入的元素进行上浮,就要需要一次次的它的祖先节点进行比较,直到找打它最合适的位置。
上浮操作核心代码如下:
private void swim(int k) {
while (k > 1 && less(k/2,k)) {
exch(k/2, k);
k = k/2;
}
}
删除堆顶元素后进行有序化
在堆排序中,我们是如何处理删除堆顶元素的呢?我们首先将堆顶元素与序列末端元素进行交换,然后删除末端元素。这是堆顶元素肯定不是堆中最大的元素,所以他需要找到他合适的位置。

为值为6的元素找到其合适位置,它需要和它的子节点中较大的节点进行交换来修复堆,但是可能交换后X还是很小,所以我们需要X一次次的它的子节点进行比较并交换,直到找打它最合适的位置。
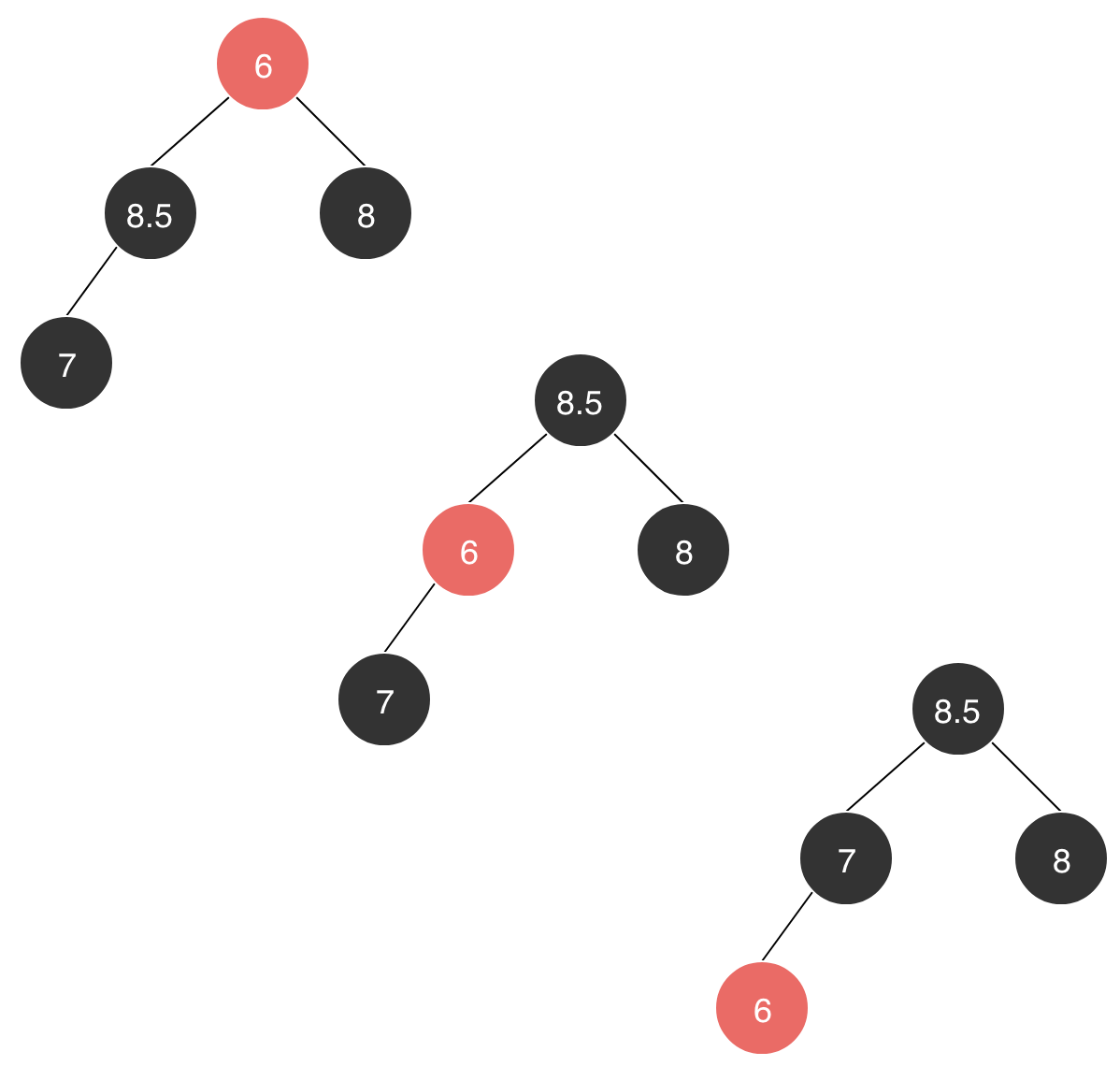
这是一种下沉操作,即被交换后的元素,需要一次次的它的子节点进行比较并交换,直到找打它最合适的位置。
下沉操作核心代码如下:
private void sink(int k) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && less(j, j + 1)) {
j++;
}
if (!less(k, j)) {
break;
}
exch(k, j);
k = j;
}
}
到这里位置,我们已经学会了在堆中插入一个新元素和删除堆顶元素的操作,这已然是堆排序的核心内容了。
Java版本实现代码
class MaxPQ<Key extends Comparable<Key>> {
private Key[] pq;
private int N = 0;
public MaxPQ(int maxN) {
pq = (Key[]) new Comparable[maxN + 1];
}
public static void main(String[] args) {
MaxPQ<Integer> maxPQ = new MaxPQ<Integer>(10);
for(int i = 0; i < 10; i++)
{
maxPQ.insert((int)(Math.random() * 10 + 1));
}
while(!maxPQ.isEmpty())
{
System.out.println(maxPQ.delMax());
}
}
public int size() {
return N;
}
public boolean isEmpty() {
return N == 0;
}
public void insert(Key v) {
pq[++N] = v;
swim(N);
}
public Key delMax() {
Key max = pq[1];
exch(1,N--);
pq[N + 1] = null;
sink(1);
return max;
}
private boolean less(int i, int j) {
return pq[i].compareTo(pq[j]) < 0;
}
private void exch(int i, int j) {
Key temp = pq[i];
pq[i] = pq[j];
pq[j] = temp;
}
private void sink(int k) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && less(j, j + 1)) {
j++;
}
if (!less(k, j)) {
break;
}
exch(k, j);
k = j;
}
}
private void swim(int k) {
while (k > 1 && less(k/2,k)) {
exch(k/2, k);
k = k/2;
}
}
}


