人工智能实战_第六次作业_廖盈嘉

第6次作业：调参

项目	内容
这个作业属于哪个课程	人工智能实战2019
这个作业的要求在哪里	人工智能实战第六次作业
我在这个课程的目标是	学会、理解和应用神经网络知识来完成一个app
这个作业在哪个具体方面帮助我实现目标	了解神经网络隐层的工作原理，学会搜索最优学习率并进行调参
作业正文	作业正文
参考文献	搜索最优学习率, Learning Rate Schedules and Adaptive Learning Rate Methods for Deep Learning

一、作业内容

---

a. 将模型准确度调整至>97%
b. 整理形成博客，博客中给出参数列表和对应值
c. 给出最终的loss下降曲线
d. 给出最终准确度结果

二、作业正文

---

a. 将模型准确度调整至>97%

1) 搜索最优学习率
由于我们不能够盲目的调节神经网络的参数，所以首先进行了最优学习率的搜索。
部分代码：

if iteration % 100 == 0:
                if (learning_rate >=0.0001) and (learning_rate<0.001):
                    learning_rate = learning_rate + 0.0001
                elif (learning_rate >=0.001) and (learning_rate<0.010):
                    learning_rate = learning_rate + 0.001
                elif (learning_rate >=0.01) and (learning_rate<0.1):
                    learning_rate = learning_rate + 0.01
                elif (learning_rate >=0.1) and (learning_rate<1):
                    learning_rate = learning_rate + 0.1
                elif (learning_rate >=1) and (learning_rate<1.1):
                    learning_rate = learning_rate + 0.01

输出图：



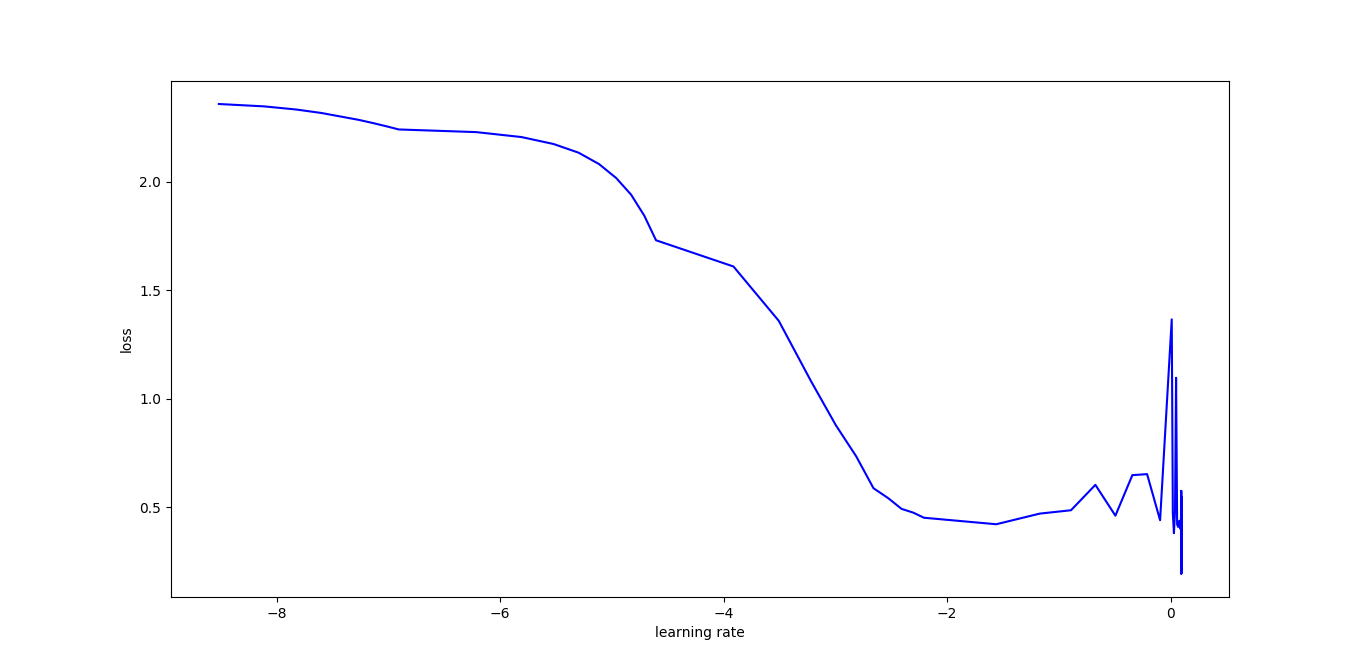
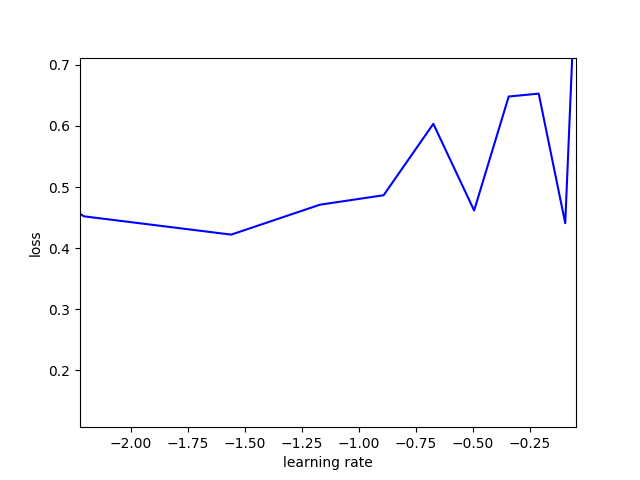
   从上图，可以看出对此模型的最优学习率为$10^{-0.5}$= 0.316227。【图中的横坐标为对数坐标轴】

2) 学习率衰减 Learning Rate Decay
随着迭代次数增加，学习率会逐渐进行减小，保证模型在训练后期不会有太大的波动，从而更加接近最优解。

learning_rate = learning_rate * np.exp(-0.01*epoch)

### b. 整理形成博客，博客中给出参数列表和对应值 适当的增加神经网络的神经元个数将会影响迭代的速度和准确度，所以选择 n_hidden1 = [128, 64, 32]; n_hidden2 = [64, 32, 16]; max_epoch = 40; learning_rate = 0.316227; batch_size = [10, 20, 30]。 一共会组成18个组合。

参数列表和对应值

number	Learning rate	mini batch	max-epoch	n_hidden1	n_hidden2	Accuracy
1	0.316227	10	40	128	64	0.983（max）
2	0.316227	20	40	128	64	0.9821
3	0.316227	30	40	128	64	0.9797
4	0.316227	10	40	128	32	0.9822
5	0.316227	20	40	128	32	0.9811
6	0.316227	30	40	128	32	0.9798
7	0.316227	10	40	128	16	0.981
8	0.316227	20	40	128	16	0.9792
9	0.316227	30	40	128	16	0.981
10	0.316227	10	40	64	32	0.9782
11	0.316227	20	40	64	32	0.9771
12	0.316227	30	40	64	32	0.9781
13	0.316227	10	40	64	16	0.978
14	0.316227	20	40	64	16	0.9783
15	0.316227	30	40	64	16	0.9771
16	0.316227	10	40	32	16	0.9685（不符合）
17	0.316227	20	40	32	16	0.9709
18	0.316227	30	40	32	16	0.969（不符合）

### c. 给出最终的loss下降曲线 | learning rate = 0.316227, max_epoch = 40, batch_size = 10, n_hidden1 = 128, n_hidden2 = 64, accuracy = 0.983 | | :----------: | |  |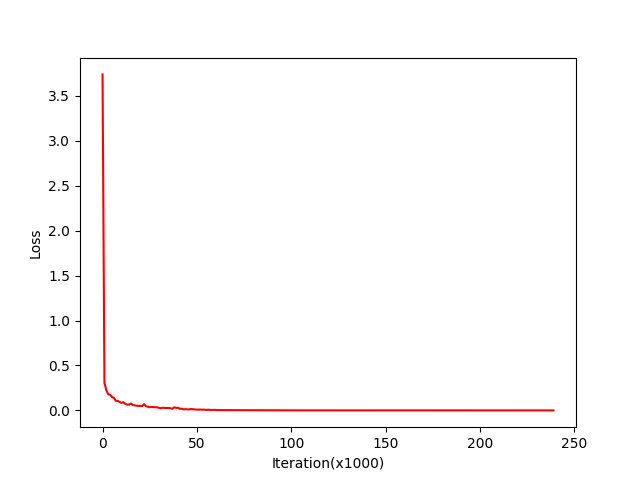
### d. 给出最终准确度结果 当learning rate = 0.316227, max_epoch = 40, batch_size = 10, n_hidden1 = 128, n_hidden2 = 64 时，给出的准确率高达0.983，是所有训练得出的数据中最高的。 在这个模型当中，当隐层的神经元个数增加时，准确率会提高，说明并没有过拟合。当神经网络隐层神经元个数较大与mini batch size较小时，准确率会提高。相反地，当神经网络隐层的神经元个数较小与mini batch size较大时，准确率会下降。