前缀，中缀，后缀表达式学习笔记(1)
2012-05-02 16:40 MichaelYin 阅读(9040) 评论(2) 编辑 收藏 举报- 表达式简介
最近看书的时候接触到了后缀表达式，恰好看SICP中间也碰到了类似的问题，就花时间好好将这部分内容进行了整理。
前缀表达式(Prefix Notation)是指将运算符写在前面操作数写在后面的不包含括号的表达式，而且为了纪念其发明者波兰数学家Jan Lukasiewicz所以前缀表达式也叫做“波兰表达式”。比如- 1 + 2 3
后缀表达式(Postfix Notation)与之相反，是指运算符写在操作数后面的不含括号的算术表达式，也叫做逆波兰表达式。比如1 2 3 + -
中缀表达式(Infix Notation)就是常用的将操作符放在操作数中间的算术表达式。前缀表达式和后缀表达式相对于中缀表达式最大的不同就是去掉了表示运算优先级的括号，比如1-2+3
现在让我们先回想一下小学数学中关于中缀表达式求值的相关的规则：
1 有括号的情况下，先计算括号内，再计算括号外
2 在无括号的情况下，考虑运算的优先级，先乘除，后加减
3 同样优先级的情况下，从左至右进行计算
在中缀表达式的情况下求值，既要考虑括号，优先级，还要考虑操作出现的先后顺序。但是，作为计算机，其计算过程就显的比较复杂，对于一个中缀表达式，需要不停地对表达式进行多次遍历，来查找相应的计算的信息。这样从算法复杂度上来说，是不可取的。
前缀表达式和后缀表达式相对于人们常用的中缀表达式最大的不同就在于表达式中的运算符是按照一定的顺序出现（接下来会具体讲解），所以求值过程中并不需要在表达式中使用括号来指定运算顺序，也不需要在计算过程中其中考虑运算符号的优先级。在采用辅助数据结构的情况下，只需要对表达式进行一次遍历即可计算出结果，大大降低了算法复杂度，也更加符合传统计算机的工作方式。
- 表达式的转换
在对前缀中缀和后缀表达式进行了简单的介绍以后，接下来对表达式之间的转换进行一个简单的阐述，在这里首先以中缀表达式转换后缀表达式为例进行较详细的讲解。
首先介绍一个人工转换的方法，假设有一个中缀表达式a+b*c-(d+e)
1首先将这个中缀表达式的所有运算加括号((a+(b*c))-(d+e))
2然后将所有运算符放到括号后面，这样就变成了((a(bc)* )+ (de)+ )-
3把所有括号去掉abc*+de+-，最后得出的结果就是后缀表达式
上面这个方法可以在比如做题分析的时候用人脑的时候使用，接下来介绍用程序实现将中缀转换成后缀表达式的思路
1 建立一个栈，然后从左至右的遍历中缀表达式
2 如果碰到了操作数，则直接将其输出，如果碰到了操作符，这个时候则需要进行优先级的比较，如果栈为空或者栈顶的操作符的优先级比当前的低，则将当前的操作符Push入栈，如果栈顶操作符比当前的操作符的优先级高或者相同，则POP操作符并输出，直到出现前一种情况为止
3 需要注意的是对于括号需要另外注意一下，如果是’(’，则直接入栈，如果是)则要找到对应的’(’为止，并且当两者同时出现时则同时删除
下面模拟程序对a+b*c-(d+e)求中缀表达式，首先对其进行扫描
输出 a 栈底 栈顶
输出 a 栈底 + 栈顶
输出 a b 栈底 + 栈顶
输出 a b 栈底 + * 栈顶
输出 a b c 栈底 + * 栈顶
输出 a b c * 栈底 + 栈顶
输出 a b c * + 栈底 - 栈顶
输出 a b c * + 栈底 - ( 栈顶
输出 a b c * + d 栈底 - ( 栈顶
输出 a b c * + d 栈底 - ( + 栈顶
输出 a b c * + d e 栈底 - ( + 栈顶
输出 a b c * + d e + 栈底 ( 栈顶
输出 a b c * + d e + - 栈底 栈顶
上面已经把中缀表达式转换后缀表达式的过程讲解了一下，而中缀表达式转换前缀表达式其实过程和转换后缀表达式及其相似，在这里就不说具体过程了，只是对其中的几个不同之处稍微说明一下：
1 转换后缀表达式由于符号是要在操作数后面出现，所以操作数入栈，扫描顺序是从左向右，转换前缀表达式的话操作符需要在操作数前面出现，那么扫描顺序就应该是从右向左。
2 操作符的具体处理方式和转换到后缀表达式略有不同
3 括号的操作也是’)’直接入栈，’(’则配对’)’后一起出栈
- 前缀，中缀，后缀表达式与二叉树的表示
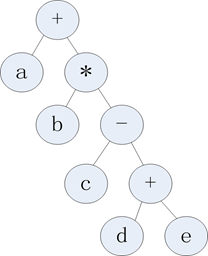
这三个表达式其实与二叉树是有这很紧密的联系的，a+b*c-(d+e)这个中缀表达式我们将其操作符当做内节点，操作数当做叶子节点，这样的话就能够画出这个中缀表达式所对应的二叉树
如果我们对这个中缀表达式进行前序和后序遍历，则输出的结果就是其对应的前缀和后缀表达式。
本篇Blog我所参考的资料
