20162309《程序设计与设计结构》第三次实验报告
实验名称:排序与查找
实验目的:对教材排序和查找内容进行补充,参考博客内容对相关方法进行实现,对已经实现的代码进行重构和打包,并结合这两周所学习的关于树、堆、桶等知识进行组合,学以致用。
实验要求:
1.完成教材P302 Searching.Java ,P305 Sorting.java中方法的测试
不少于10个测试用例,提交测试用例设计情况(正常,异常,边界,正序,逆序),用例数据中要包含自己学号的后四位
2.重构你的代码
把Sorting.java Searching.java放入 cn.edu.besti.cs1623.(姓名首字母+四位学号) 包中
把测试代码放test包中
重新编译,运行代码,提交编译,运行的截图(IDEA,命令行两种)
3.对searching类进行方法的补充,添加顺序、分块、树表、二分、插值、哈希、斐波那契等几种查找方法,并进行测试。
4.补充实现课上讲过的排序方法:希尔排序,堆排序,桶排序,二叉树排序等
测试实现的算法(正常,异常,边界)
实验日期:2017.11.6
指导老师:娄老师、王老师
实验过程:
1.对教材上的Searching和Sorting类进行编译,教程中这两个类已经基本实现了方法,只需要编写一个测试类,测试运行即可。这里的测试类可以通过定义整型数来实现,需要使用integer方法,通过if语句来判断查找的返回值,并输出结果:
String found = new String();
if (found == null)
System.out.println("");
else
System.out.println(" " + found);
这里可以看出,当查找的内容不存在时,会返回空。
integer整数值的代码:
Integer[] n = {23,38,12,34,254,86,91,116,144,149,120,2309};
Integer o = (Integer) Searching.linearSearch(n, 3);
Integer p = (Integer) Searching.linearSearch(n, 8);
Integer q = (Integer) Searching.linearSearch(n, 2309);
Integer r = (Integer) Searching.linearSearch(n, 120);
Integer s = (Integer) Searching.linearSearch(n, 12);
Integer t = (Integer) Searching.linearSearch(n, 91);
查找部分可以通过此方法实现。
排序部分的实现方法是通过比较长度来判断顺序的,具体实现方法如下:
for (int i = 0; i < n1.length; i++)
System.out.print(n1[i]+" ");
System.out.println();
sorting.selectionSort(n2);
for (int i = 0; i < n2.length; i++)
System.out.print(n2[i]+" ");
System.out.println();
sorting.insertionSort(n3);
for (int i = 0; i < n3.length; i++)
System.out.print(n3[i]+" ");
System.out.println();
sorting.mergeSort(n5,3,n5.length-1);
for (int i = 0; i < n5.length; i++)
对输入的数进行判断即可实现方法。

2.重构代码,将代码分别导入到包内,并重新测试,同时需要在cmd命令行下运行。
这个过程就相对比较简单了,在idea方便的操作系统下,只需要在src目录下新建一个包,再将相应的java文件拖进去就可以了。
同时在命令行下运行和在idea上运行没有太大的区别,只是需要编译过程,这里可以使用mkdir命令新建一个文件夹,在新建的目录里运行
3.实验3的内容相对较多,需要补充较多的方法,根据博客内容进行改进。
实验三是对searching类的改进,分别需要补充顺序、树表、分块、斐波那契、二分、哈希、插值这几种查找方法,博客里给到了实现思路和c语言的实现方法,作为java语言的类比,可以对这些方法进行编写。
代码实现过程(关键部分):
private static int Insert_Search(int[] num, int key) {
int low, high, mid;
low = 0;
high = num.length - 1;
while (low <= high) {
mid = low + (high - low) * (key - num[low])/ (num[high] - num[low]);
// 插值查找
if (key < num[mid])
high = mid - 1;
else if (key > num[mid])
low = mid + 1;
else
return mid;
}
return -1;
}
public final static int MAXSIZE = 20;
插值查找的实现可以通过上述方法,首先需要了解插值查找的基本原理:
首先考虑一个新问题,为什么一定要是折半,而不是折四分之一或者折更多呢?
打个比方,在英文字典里面查“apple”,你下意识翻开字典是翻前面的书页还是后面的书页呢?如果再让你查“zoo”,你又怎么查?很显然,这里你绝对不会是从中间开始查起,而是有一定目的的往前或往后翻。
同样的,比如要在取值范围1 ~ 10000 之间 100 个元素从小到大均匀分布的数组中查找5, 我们自然会考虑从数组下标较小的开始查找。
经过以上分析,折半查找这种查找方式,还是有改进空间的,并不一定是折半的!
mid = (low+high)/ 2, 即 mid = low + 1/2 * (high - low);
改进为下面的计算机方案(不知道具体过程):mid = low + (key - a[low]) / (a[high] - a[low]) * (high - low),也就是将上述的比例参数1/2改进了,根据关键字在整个有序表中所处的位置,让mid值的变化更靠近关键字key,这样也就间接地减少了比较次数。
分析:从时间复杂度上来看,它也是o(n),但是对于表长较大,而关键字分布又比较均匀的查找表来说,插值查找算法的平均性能比折半查找要好的多。反之,数组中如果分布非常不均匀,那么差值查找未必是很合适的选择。
插值查找是一种有序查找,需要判断有序,关键实现方法也是需要if判断语句:‘
mid = low + (high - low) * (key - num[low])/ (num[high] - num[low]);
if (key < num[mid])
high = mid - 1;
else if (key > num[mid])
low = mid + 1;
else
这里如果等于则直接还回下标值 ,则为:
return mid;
}
return -1;
}
}
在输入数组后就可以运行了。
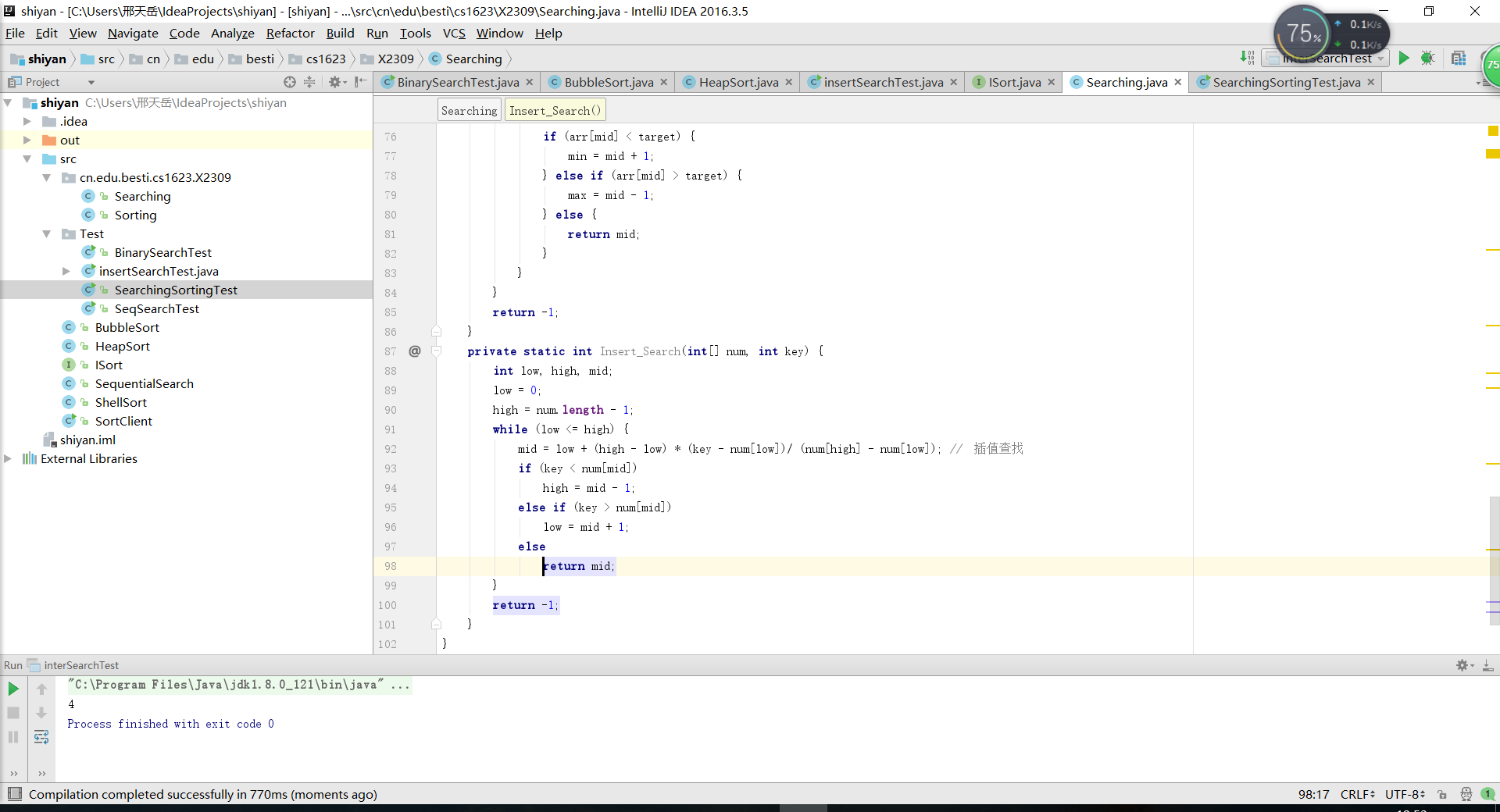
其次的一个关键点是斐波那契查找,受限需要了解什么是斐波那契查找:
斐波那契数列,又称黄金分割数列,指的是这样一个数列:1、1、2、3、5、8、13、21、····,在数学上,斐波那契被递归方法如下定义:F(1)=1,F(2)=1,F(n)=f(n-1)+F(n-2) (n>=2)。该数列越往后相邻的两个数的比值越趋向于黄金比例值(0.618)。
斐波那契查找就是在二分查找的基础上根据斐波那契数列进行分割的。在斐波那契数列找一个等于略大于查找表中元素个数的数F[n],将原查找表扩展为长度为Fn,完成后进行斐波那契分割,即F[n]个元素分割为前半部分F[n-1]个元素,后半部分F[n-2]个元素,找出要查找的元素在那一部分并递归,直到找到。
斐波那契查找的时间复杂度还是O(log 2 n ),但是 与折半查找相比,斐波那契查找的优点是它只涉及加法和减法运算,而不用除法,而除法比加减法要占用更多的时间,因此,斐波那契查找的运行时间理论上比折半查找小,但是还是得视具体情况而定。
对于斐波那契数列:1、1、2、3、5、8、13、21、34、55、89……(也可以从0开始),前后两个数字的比值随着数列的增加,越来越接近黄金比值0.618。比如这里的89,把它想象成整个有序表的元素个数,而89是由前面的两个斐波那契数34和55相加之后的和,也就是说把元素个数为89的有序表分成由前55个数据元素组成的前半段和由后34个数据元素组成的后半段,那么前半段元素个数和整个有序表长度的比值就接近黄金比值0.618,假如要查找的元素在前半段,那么继续按照斐波那契数列来看,55 = 34 + 21,所以继续把前半段分成前34个数据元素的前半段和后21个元素的后半段,继续查找,如此反复,直到查找成功或失败,这样就把斐波那契数列应用到查找算法中了。
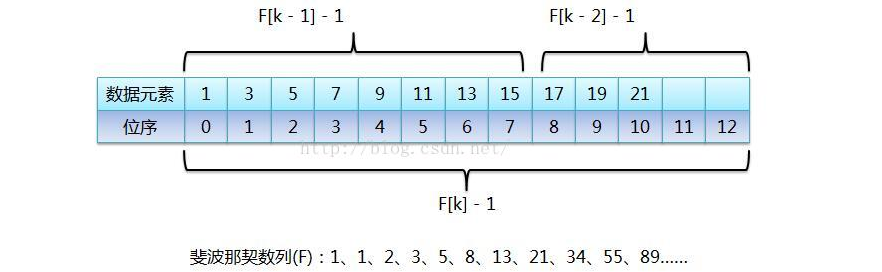
从图中可以看出,当有序表的元素个数不是斐波那契数列中的某个数字时,需要把有序表的元素个数长度补齐,让它成为斐波那契数列中的一个数值,当然把原有序表截断肯定是不可能的,不然还怎么查找。然后图中标识每次取斐波那契数列中的某个值时(F[k]),都会进行-1操作,这是因为有序表数组位序从0开始的,纯粹是为了迎合位序从0开始。
实际上的代码实现:
public static int[] fibonacci(){
int[] f = new int[20];
int i =0;
f[0] = 1;
f[1] = 1;
for(i=2;i<MAXSIZE;i++){
f[i] = f[i-1]+f[i-2];
}
return f;
}
首先需要定义斐波那契数组,需要定义长度。
然后是具体的方法实现:
public static int fibonacciSearch(int[] data,int key){
int low = 0;
int high = data.length-1;
int mid = 0;
int k = 0;
int i=0;
int[] f = fibonacci();
while(data.length>f[k]-1){
k++;
}
和二叉查找树类似,定义一个key值可以便于方法的实现,在比较长度的方法上,斐波那契查找重点是需要确定查找元素的位置,在比较过程中,key值的作用就可以体现出来了:
for(i=data.length;i<f[k]-1;i++){
temp[i]=temp[high];
}
for(int j:temp){
System.out.print(j+" ");
}
System.out.println();
while( low <= high )
{
mid = low + f[k-1] - 1;
写完测试类就可以运行了:
二分、分块在时现方法上是一个递进的过程,实现过程可以类比。希尔查找需要用到希尔函数,在使用上可以建立希尔函数,同样可以输入key值,通过位置查找:
public static int searchHash(int[] hash, int hashLength, int key) {
// 哈希函数
int hashAddress = key % hashLength;
while (hash[hashAddress] != 0 && hash[hashAddress] != key) {
hashAddress = (++hashAddress) % hashLength;
}
if (hash[hashAddress] == 0)
return -1 ;
return hashAddress;
}
定义函数后,方法就很好实现了。
4.关于排序的补充:
实验四是对排序方法的各种补充,包括桶排序、堆排序、希尔排序和二叉树排序,几种排序方法都可以通过教材上的相关方法实现。
首先是最近课上所补充的堆排序方法:
同样需要先设一个范围(heapsize)

然后需要建立堆,以及最大堆:
public void BuildMaxHeap()
{
for(int i=heapsize/2-1;i>=0;i--)
{
Maxify(i);
}
}
public void HeapSort()
{
for(int i=0;i<heap.length;i++)
{
int tmp=heap[0];
heap[0]=heap[heapsize-1];
heap[heapsize-1]=tmp;
heapsize--;
Maxify(0);
}
}
接下来就是通过比较进行排序的过程了,同样需要和最大值进行比较:
int l=Left(i);
int r=Right(i);
int largest;
if(l<heapsize&&heap[l]>heap[i])
largest=l;
else
largest=i;
if(r<heapsize&&heap[r]>heap[largest])
largest=r;
if(largest==i||largest>=heapsize)
return ;
int tmp=heap[i];
heap[i]=heap[largest];
heap[largest]=tmp;
Maxify(largest);
最后是定义返回值,得到结果:
private int Parent(int i)
{
return (i-1)/2;
}
private int Left(int i)
{
return 2*(i+1)-1;
}
private int Right(int i)
{
return 2*(i+1);
}
桶排序也可以借鉴上面的过程,只是方法需要改变,使用桶排序的方法;
桶排序 (Bucket sort)或所谓的箱排序,是一个排序算法,工作的原理是将阵列分到有限数量的桶子里。每个桶子再个别排序(有可能再使用别的排序算法或是以递回方式继续使用桶排序进行排序)。桶排序是鸽巢排序的一种归纳结果。当要被排序的阵列内的数值是均匀分配的时候,桶排序使用线性时间(Θ(n))。但桶排序并不是 比较排序,他不受到 O(n log n) 下限的影响。
两个特征:
待排序列所有的值处于一个可枚举的范围之类;
待排序列所在的这个可枚举的范围不应该太大,否则排序开销太大。
排序的具体步骤如下:
(1)对于这个可枚举范围构建一个buckets数组,用于记录“落入”每个桶中元素的个数;
(2)将(1)中得到的buckets数组重新进行计算,按如下公式重新计算:
buckets[i] = buckets[i] +buckets[i-1] (其中1<=i<buckets.length);
桶式排序是一种非常优秀的排序算法,时间效率极高,它只要通过2轮遍历:第1轮遍历待排数据,统计每个待排数据“落入”各桶中的个数,第2轮遍历buckets用于重新计算buckets中元素的值,2轮遍历后就可以得到每个待排数据在有序序列中的位置,然后将各个数据项依次放入指定位置即可。
实验具体实现方法:
public static void bucketSort(int[] a, int max) {
int[] buckets;
if (a==null || max<1)
return ;
buckets = new int[max];
for(int i = 0; i < a.length; i++)
buckets[a[i]]++;
for (int i = 0, j = 0; i < max; i++) {
while( (buckets[i]--) >0 ) {
a[j++] = i;
}
}
buckets = null;
}
在编写完测试类后就可以运行了
完成了测试后就可以很得到结果了。
实验总结:这次实验总体上是对学过知识的回顾和整合,并和最近所学的新内容相结合,总体上起到了一个系统考察的效果。




