[大整数乘法]分治算法的时间复杂度研究
开篇
最近研究分治算法，对大整数算法（包括加减乘数）、strassen矩阵乘法、合并排序的优化、线性时间选择和最接近点对问题学习了一下。
这篇文章主要是关于大整数乘法算法复杂度的研究。
本人菜鸟，本科就读北京一工科院校土建专业，现就读北京一所二流985的计算机研究生。
希望在这里分享和学习，如有错误还请多多指点！
正文
一，引入问题
在某些情况下，我们需要计算很大的整数，它无法在计算机硬件能直接表示的整数范围内进行处理，如果用浮点数则会有精度问题，这就必须用软件的方法来实现大整数的算术运算。
二，大整数乘法的分治解决方案
2.1原始低效算法
我们将n位（为方便讨论简化问题，我们假设n是2的幂）十进制整数（二进制也可以）X、Y都分为2段，每段的长度是n/2位。
如果现在直接用递归或分治进行编程，其算法复杂度为：
其中：T(n)代表规模为n的问题，系数4表示问题缩小到T(n/2)时，包含四次乘法（上式中AC/AD/BC/BD四次）
这是在没有进行优化情况下的算法复杂度（注意，此处虽然用了分治思想，但分治并不会降低算法复杂度，反而因其需要使用栈，增加了算法的空间复杂度）。
2.2如何进行优化降低复杂度？
我们知道，大整数乘法的基本运算是“乘法”运算，我们可以通过减少乘法的次数来降低算法复杂度！
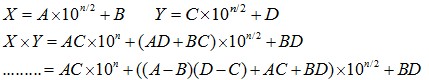
从公式中可以发现，原来有四个基本乘积项：AC、AD、BC、BD，现在只有三个基本乘积项：（A-B)(C-D)、AC、BD。乘法运算的数量降低了，下面看看其复杂度变化：
复杂度从n2降到n1.59
三，时间复杂度还能优化吗？
3.1上面讨论中，我们将大整数X、Y都分为2段，每段的长度是n/2位，那分成3段4段会如何？
3.1.1大整数分3段：
3.2.2大整数分4段：
3.2.3大整数分n段：
结论：
在大整数乘法中，当把大整数分为2段时，算法时间复杂度最低n1.59
随着段数逐渐增加，算法的时间复杂度也随之增加，当分段增加到n段时，算法时间复杂度退化到n2
3.2算法复杂度还能降低吗？
用快速傅里叶变换只需要O(N*logN)的时间复杂度！（该部分后续添加）
四，编程思想
本人用java实现了大整数乘法的计算，代码部分会另起一篇，以下是连接：
http://www.cnblogs.com/McQueen1987/p/3401979.html
