【codevs1743】 反转卡片

http://codevs.cn/problem/1743/ (题目链接)

题意

　　给出一个序列{a₁,a₂,a₃···}，要求维护这样一种操作：将前a₁个数反转，若第a₁等于1，则停止操作。

Solution

 

　　像这种带有反转区间的操作，大概就是splay了。码了一个晚上。。。

　　splay一般就是处理区间反转，区间插入，区间删除这三种线段树等数据结构无法处理的操作，splay难写又难调，经常犯一些鬼畜错误，能不写就尽量不写的好。。splay不是二叉搜索树，但它有一个很优秀的性质：树的中序遍历出来的序列就是原始序列。这样我们方便的就可以处理区间上的问题，比如说对于区间[l,r]，我们将l-1splay到树根，将r+1splay到树根的右儿子，那么我们要修改的区间就是树根的右儿子的左儿子子树。

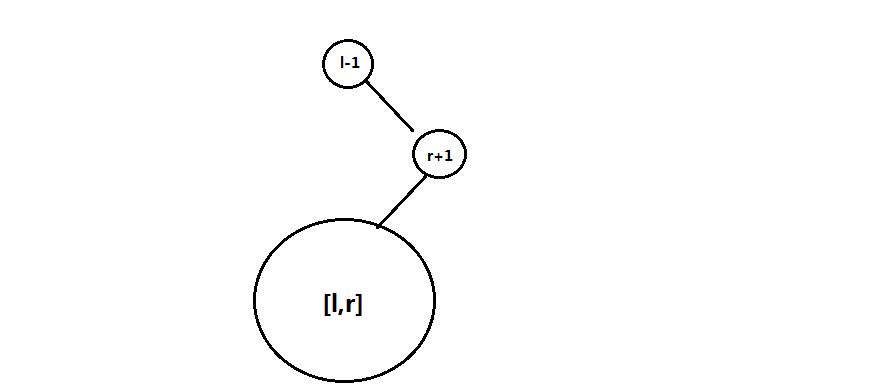
　　所以对于这道题，我们每次反转时，先将splay两遍，然后再给节点[l,r]打上标记即可。代码模着hzwer写的，感觉很优秀。

代码

// codevs1743
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LL long long
#define inf 2147483640
#define Pi acos(-1.0)
#define free(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout);
using namespace std;

const int maxn=300010;
int a[maxn],tr[maxn][2],fa[maxn],size[maxn],val[maxn],rev[maxn];
int n,ans,rt;

void rotate(int x,int &k) {
	int y=fa[x],z=fa[y],l,r;
	if (x==tr[y][0]) l=0;else l=1;
	r=l^1;
	if (y==k) k=x;
	else tr[z][tr[z][1]==y]=x;
	fa[y]=x;fa[x]=z;fa[tr[x][r]]=y;
	tr[y][l]=tr[x][r];tr[x][r]=y;
	//注意这里一定先更新y的size,再更新x的size.
	size[y]=size[tr[y][0]]+size[tr[y][1]]+1;
	size[x]=size[tr[x][0]]+size[tr[x][1]]+1;
}
void splay(int x,int &k) {
	while (x!=k) {
		int y=fa[x],z=fa[y];
		if (y!=k) {   //如果x,y,z在一条链(形象)上,那么先旋y,再旋x.听说可以使平衡树更加平衡
			if (tr[z][0]==y ^ tr[y][0]==z) rotate(x,k);   //不在一条链上
			else rotate(y,k);   //在一条链上
		}
		rotate(x,k);
	}
}
void pushdown(int k) {
	int l=tr[k][0],r=tr[k][1];
	rev[k]^=1;rev[l]^=1;rev[r]^=1;   //如果同一个区间被反转2次,那么就等价于不反转.
	swap(tr[k][0],tr[k][1]);
}
int find(int k,int x) {   //在树中寻找序列中第rk个数
	if (rev[k]) pushdown(k);
	int l=tr[k][0],r=tr[k][1];
	if (size[l]+1==x) return k;
	else if (x<=size[l]) return find(l,x);
	else return find(r,x-size[l]-1);
}
void build(int l,int r,int f) {
	if (l>r) return;
	int mid=(l+r)>>1;
	//tr[][]记录当前节点的左儿子与右儿子
	if (mid<f) tr[f][0]=mid;
	else tr[f][1]=mid;
	//size[]记录子树大小,val[]记录数值,fa[]记录父亲.
	rev[mid]=0;val[mid]=a[mid];size[mid]=1;fa[mid]=f;
	if (l==r) return;
	build(l,mid-1,mid);
	build(mid+1,r,mid);
	size[mid]=size[tr[mid][0]]+size[tr[mid][1]]+1;
}
void rever(int l,int r) {
	int x=find(rt,l),y=find(rt,r+2);
	splay(x,rt);splay(y,tr[rt][1]);
	rev[tr[y][0]]^=1;
}
int main() {
	scanf("%d",&n);
	for (int i=1;i<=n;i++) scanf("%d",&a[i+1]);
	build(1,n+2,0);rt=(3+n)>>1;
	int ans=0;
	while (val[find(rt,2)]!=1) {
		ans++;
		rever(1,val[find(rt,2)]);
		if (ans>100000) {printf("-1");return 0;}
	}
	printf("%d",ans);
	return 0;
}