【bzoj1005】 HNOI2008—明明的烦恼

http://www.lydsy.com/JudgeOnline/problem.php?id=1005 (题目链接)

题意

　　给出标号为1到N的点,以及某些点最终的度数，允许在任意两点间连线，可产生多少棵度数满足要求的树？

Solution 

　　prufer编码。关于prufer，有一篇博客写得很好，还运用组合数学求出了公式，可惜代码是java。这道题还要写高精度，高精度除法太麻烦了，因为组合数一定是整数，所以我们选择将n！分解质因数，最后相加减就可以了。如何分解质因数呢，我当然不会去暴力分解，一次考试中就是暴力分解TLE了= =。 

　　若P为质数，则n!可分解为 一个数×P^x。其中 
　　 

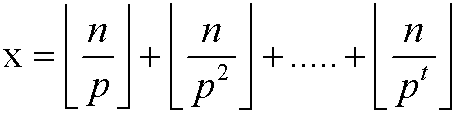
　　并且P^t小于n，所以就很好做了。

代码

// bzoj1005
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<map>
#define inf 2147483640
#define LL long long
#define free(a) freopen(a".in","r",stdin);freopen(a".out","w",stdout);
using namespace std;
inline LL getint() {
    LL x=0,f=1;char ch=getchar();
    while (ch>'9' || ch<'0') {if (ch=='-') f=-1;ch=getchar();}
    while (ch>='0' && ch<='9') {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}

const int maxn=10010;
int ans[maxn*100],np[maxn],a[maxn],d[maxn];
int l=1,n,sum;

void pls(int x,int f) {
    for (int i=2;i<=x;i++)
        if (!np[i]) for (int j=i;j<=x;j*=i) a[i]+=f*x/j;
}
void mul(int x) {
    for (int i=1;i<=l;i++) ans[i]*=x;
    for (int i=1;i<=l;i++) {
        ans[i+1]+=ans[i]/10;
        ans[i]%=10;
    }
    while (ans[l+1]>0) {l++;ans[1+l]+=ans[l]/10;ans[l]%=10;}
}
int main() {
    for (int i=2;i<=1000;i++) if (!np[i]) {
            int x=i+i;
            while (x<=1000) np[x]=1,x+=i;
        }
    scanf("%d",&n);
    if (n==1) {
        int x;scanf("%d",&x);
        if (!x) printf("1");
        else printf("0");
        return 0;
    }
    int cnt=0;ans[1]=1;
    for (int i=1;i<=n;i++) {
        scanf("%d",&d[i]);
        if (!d[i]) {printf("0");return 0;}
        if (d[i]>0) {d[i]--;sum+=d[i];}
        else cnt++;
    }
    if (sum>n-2) {printf("0");return 0;}
    pls(n-2,1);
    pls(n-2-sum,-1);
    for (int i=1;i<=n;i++) if (d[i]) pls(d[i],-1);
    for (int i=2;i<=1000;i++)
        for (int j=1;j<=a[i];j++) mul(i);
    for (int i=1;i<=n-2-sum;i++) mul(cnt);
    for (int i=l;i>=1;i--) printf("%d",ans[i]);
    return 0;
}