Boosting(提升方法)之AdaBoost
集成学习(ensemble learning)通过构建并结合多个个体学习器来完成学习任务,也被称为基于委员会的学习。
集成学习构建多个个体学习器时分两种情况:一种情况是所有的个体学习器都是同一种类型的学习算法,比如都是决策树,或者都是神经网络。这样的集成是“同质”的,同质集成中的个体学习器称为“基学习器”,相应的算法称为“基学习算法”;另一种情况是集成学习中包含的个体学习器是不同类型的,比如同时包含了决策树或者神经网络算法,那么这样的集成是“异质”的,这时的个体学习器不能称为“基学习器”。
那么选择什么样的个体学习器呢?一般来说,要获得好的集成效果,个体学习器应该“好而不同”,即个体学习器的预测结果要有一定的准确性,同时各个体学习器之间要存在差异。
那么根据个体学习器的生成方式,大致可以将集成学习分为两大类:一类是个体学习器之间存在非常强的依赖关系,必须串行生成的序列化方法,代表就是Boosting(提升方法);第二类是个体学习器之间不存在强依赖关系,可同时生成的并行化方法,代表是Bagging和随机森林(Random Forest)。
因此这篇文章要整理的提升方法和AdaBoost(Adaptive Boosting)就是属于个体学习器是同一种类型的学习算法的情况,且基学习器之间存在强依赖关系,必须串行生成。
一、提升方法的总体思想
提升(boosting)方法是一种常用的统计学习方法,在分类问题中,它通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类的性能。它是基于这样一种思想:在比较复杂的任务中进行决策时,把多个专家的判断进行适当的综合所得到的判断,会比其中任何一个专家单独的判断更好。
提升的含义是,在学习中,如果已经发现了“弱学习算法”(弱学习算法是指学习到的分类器,其误差率仅仅比随机猜测要好一点的学习算法),那么可以通过某种方式把它提升为“强学习算法”。因为有学者证明了,在概率近似正确(PAC)学习的框架中,一个概念是强可学习的充要条件是这个概念是弱可学习的。进一步地来说,在分类问题中,求比较粗糙的分类规则(弱分类器)要比求精确的分类规则(强分类器)要容易得多,那么何不从弱学习分类算法出发,通过反复学习得到一系列弱分类器(或称基本分类器),然后组合这些弱分类器,构成一个强分类器呢?
那么如何得到一系列的弱分类器呢?大部分的提升方法都是每学习一个弱分类器,就改变训练数据的概率分布(训练数据的权值分布),然后针对不同的训练数据分布,调用弱学习算法学习一系列弱分类器。
于是对于提升方法来说,要解决两个问题:一是在每一轮训练中如何调整样本数据的权值或概率分布;二是如何将弱分类器组合成一个强分类器。不同的提升方法对这两个问题有不同的处理办法。
而提升方法中最具有代表性的AdaBoost算法是这样做的:
对于第一个问题,提高那些被前一轮弱分类器错误分类的样本的权值,而降低那些被正确分类的样本的权值。那么没有得到正确分类的数据,由于其权值的加大而在下一轮的训练中,受到下一个分类器更大的关注。
对于第二个问题,关于如何将一系列弱分类器组合为一个强分类器,AdaBoost采取加权多数表决的方法。具体的做法是加大分类误差率小的弱分类器的权值,使其在表决中起到较大的作用;减小分类误差率大的弱分类器的权值,使其在表决中起较小的作用。
以下是AdaBoost的概要图。分类器在加权的数据集上进行训练,接着结合起来产生最终的预测。
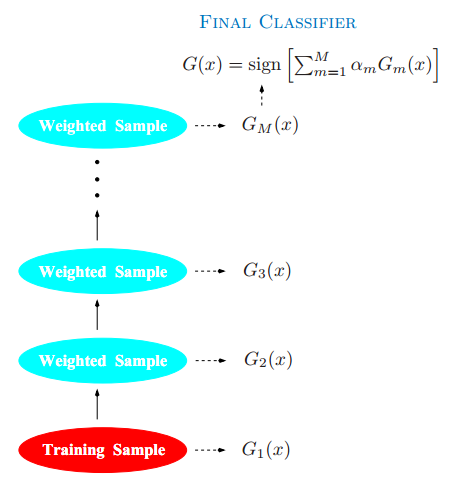
二、AdaBoost算法公式推导
已有训练数据集T={(x1,y1),(x2,y2),...,(xN,yN)}, 其中xi属于X属于Rn,yi属于y={-1, +1};选择一种弱学习算法(比如决策树),然后:
步骤1:初始化N个训练样本数据的权值分布,原始数据的权值分布是均匀的。
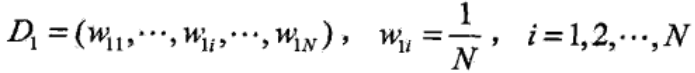
步骤2:AdaBoost反复学习基本分类器,在每一轮训练(m=1, 2, ..., M)中顺次地执行下列操作:
(1)使用具有权值分布Dm的训练数据集学习,得到第m个基本分类器,预测值是1或-1:
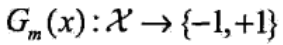
(2)计算基本分类器Gm(x)在加权训练数据集上的分类误差率:
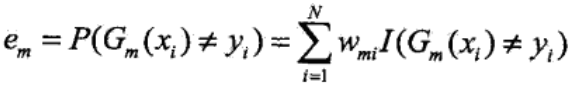
其中,wmi表示第m轮中第i个实例的权值,N个实例的权值之和为1。因此第m个基本分类器Gm(x)在加权训练数据集上的分类误差率,是被Gm(x)误分类样本的权值之和。
(3)由分类误差率计算基本分类器Gm(x)的系数(以自然对数为底):
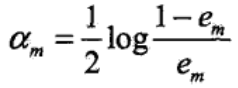
αm有两个作用,一是用来调整下一轮训练中训练数据的权值,二是用来表示基本分类器Gm(x)在最终分类器中的重要性。em以0.5为界,em≥0.5时,αm≥0,并且αm与em是呈反方向变化的,因此第m个基本分类器的分类误差率越小,在最终分类器中的作用越大。
(4)更新训练数据的权值分布,为下一次训练做准备:
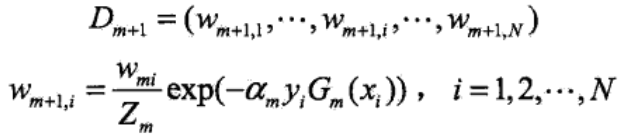
Zm是规范化因子,所以Dm+1是一个概率分布,其各元素之和为1。
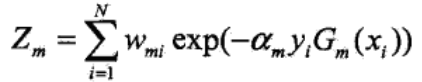
注意到yi与Gm(xi)的值取{1,-1},因此yi=Gm(xi),即样本的真实类别与基本分类器的预测类别相同时,分类正确,yiGm(xi)=1,而不相等时,yiGm(xi)=-1。于是公式也可以写成:
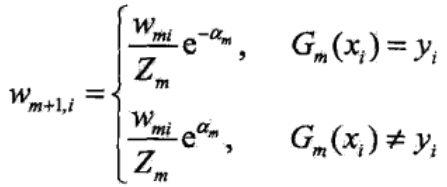
可以看到,这一轮被基本分类器Gm(x)分类错误的样本,将被赋予更高的权值,相反被分类正确的样本,权值得以缩小,而且,这两类样本之间的权值之比为e2αm。
所以AdaBoost的特点是,不改变所给的训练数据,而是改变训练数据的权值分布,使得训练数据在每一轮的基本分类器的学习中起到不同的作用。
步骤3:构建得到的M个基本分类器的线性组合,实现加权表决
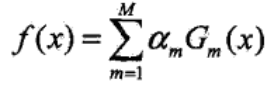
并得到最终的分类器
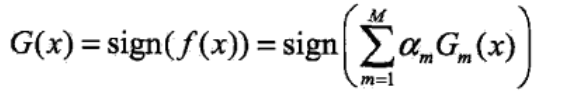
这里所有的αm之和并不为1,sign(•)是指示函数,f(x)的符号决定了样本x的类别,f(x)为正时,G(x)等于1,f(x)为负时,G(x)等于-1。
以上就是AdaBoost的一般步骤,看完后,会发现这三个步骤中有些地方是有跳跃的,一是这个基本分类器选择哪种模型(决策树、SVM还是朴素贝叶斯),二是使用权值分布Dm的训练数据集,如何进行学习来得到第m个基本分类器,甚至也没有提到损失函数。这需要更具体的算法,比如提升树来说明。当然下面会证明AdaBoost的损失函数其实是指数损失函数。
三、AdaBoost算法的另一种解释:加法模型和前向分步算法
1、加法模型和前向分步算法
(1)加法模型的定义:
加法模型的形式为
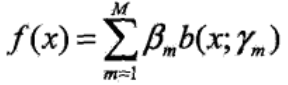
其中,b(x; γm)是基函数,γm是基函数的参数,βm是基函数的系数。
给定训练数据集和损失函数L(y, f(x))的条件下,学习加法模型f(x)就成了经验风险最小化的问题:
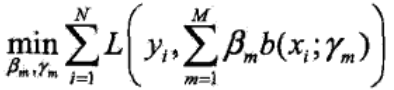
(2)加法模型的求解:前向分步算法
同时求解加法模型中的γ和β这两个参数(一共有2M个待求参数)是一件复杂的事情,可以用前向分步算法(forward stagewise algorithm)来进行求解。
前向分步算法求解这一优化问题的思路是:因为求解的加法模型是M个基函数的组合,如果能够从前到后,每次只学习一个基函数和系数(参数),逐步逼近优化目标函数式,那么就可以将复杂的问题简单化。
前向分步算法求解加法模型的具体步骤为:
步骤一:确定训练数据集为T={(x1,y1),(x2,y2),...,(xN,yN)},损失函数为L(y, f(x)),基函数集为{b(x; γ)},初始化f0(x)=0。
步骤二:对m=1, 2, ..., M,逐个求解γm、βm和基函数fm(x)。
①极小化损失函数,得到参数γm和βm:
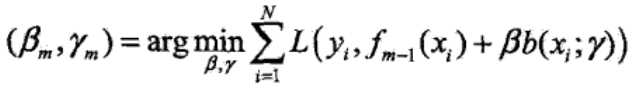
②更新基函数:
![]()
步骤三:得到M个基函数和参数γm、βm,组合成加法模型:
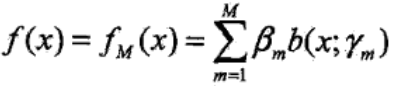
2、AdaBoost的前向分步算法
对于AdaBoost有另外一种解释,即可以认为AdaBoost是前向分步加法算法的特例,是模型为加法模型、损失函数是指数函数、学习算法是前向分步算法的二类分类学习方法。
接下来证明AdaBoost是前向分步加法算法的特例,参考的是《统计学习方法》,并将其中有跳跃的部分证明进行了细化:

参考资料:
1、李航:《统计学习方法》
2、周志华:《机器学习》
3、《The Elements of Statistical Learning》(ESL)


