20172323 2018-2019-1 《程序设计与数据结构》第七周学习总结

20172323 2018-2019-1 《程序设计与数据结构》第七周学习总结

教材学习内容总结

本周学习了第11章二叉查找树

• 11.1概述
  • 二叉查找树的左孩子小于父结点，而父结点又小于或等于其右孩子
  • 二叉查找树的定义是二叉树定义的扩展

操作	说明
addElement	往树中添加一个元素
removeElement	从树中删除一个元素
removeAllOccurrences	从树中删除所指定元素的任何存在
removeMin	删除树中的最小元素
removeMax	删除树中的最大元素
findMin	返回一个指向树中最小元素的引用
findMax	返回一个指向树中最大元素的引用

• 11.2用链表实现二叉查找树

  • 每个BinarySearchTreeNode对象要维护一个指向结点所存储元素的引用，另外还要维护指向结点的每个孩子的引用
  • addElement操作：根据给定元素值往树中恰当位置添加元素，要求元素类型是Comparable,否则抛出NoComparableElementException异常。该树为空，元素成为根结点；小于根结点但左孩子不为null将会遍历根的左孩子直到找到合适位置。
    
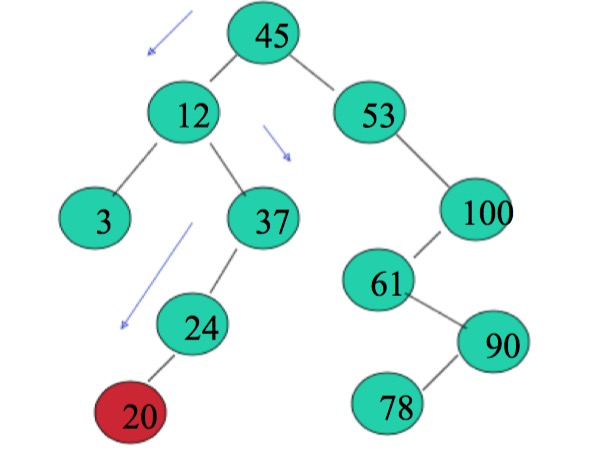
    如图，值为20的一个元素添加到该树中，比较根结点比45小，应该往左子树的方向添加，左孩子12不为null，所以又往右子树的方向往下走到37，再往左子树走，直到成为24的左子树。
  • removeElement操作：从二叉查找树中删除一个元素时，必须推选出另一结点来代替要被删除的结点。
    • 选择替换结点的三种操作
      - 如果被删除结点没有孩子，则replacement返回null
      - 如果被删除结点只有一个孩子，则replacement返回这个孩子
      - 如果被删除结点有两个孩子，则replacement会返回中序后继者
      
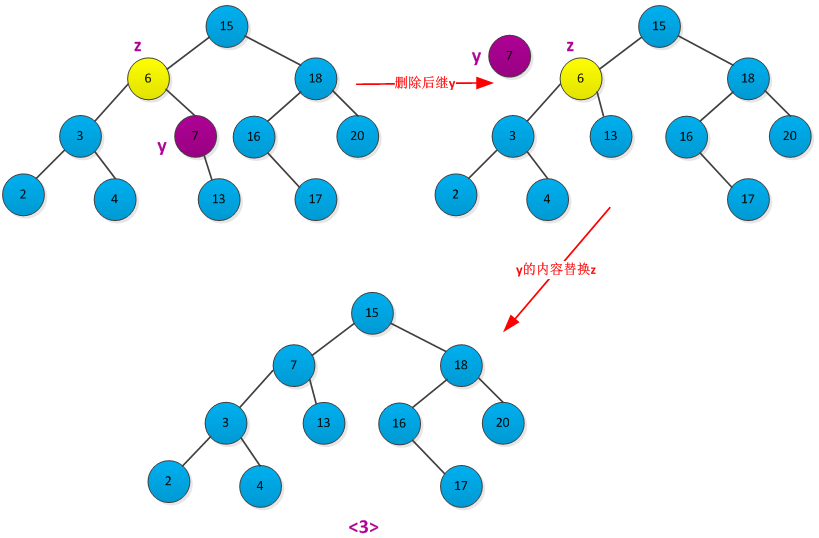
      要想删除有两个孩子的z结点，首先找到它的中序后继者y结点，将y移除，再将y结点替换z结点即可
  • removeAllOccurences操作：该方法会调用一次removeElement方法，以此确保当树中根本不存在指定元素会抛出异常
  • removeMin操作：
    最小元素在二叉查找树中的三种情况
    • 如果没有左孩子，根结点是最小元素。此时根的右孩子成为新的根结点
    • 如果树的最左侧结点是叶结点，这个根结点就是最小元素，只需设置该结点为null
    • 若树的最左端是一个内部结点，则需要设置其父结点的左孩子引用指向这个将删除结点的右孩子

• 11.3 用有序列表实现二叉查找树

  • 树的主要使用之一就是为其它集合提供高效的实现
  • BinarySearchTreeList实现中的用到的是一种带有附加属性的平衡二叉查找树，其附加属性在于：任何结点的最大深度为log2(n)，n为树中存储的元素
  • 在平衡二叉查找树假设之下，add操作和remove操作都要求重新平衡化树

• 11.4 平衡二叉查找树

  • 如果二叉查找树不平衡，其效率可能比线性结构的还要低
  • 如下是一个蜕化树的例子
    
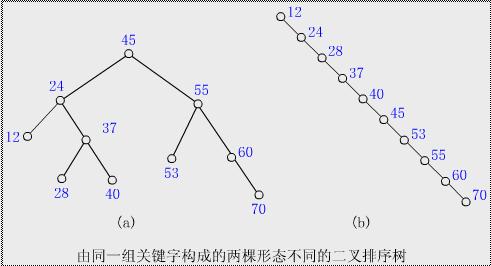
    如果没有平衡假设，在此树中添加一个大于70的元素，则它的时间复杂度将为O(n)，而我们的目标在于保持树的最大路径长度为log2(n)
  • 右旋：右旋可以解决树根左孩子的左子树中较长的路径而导致的不平衡
    

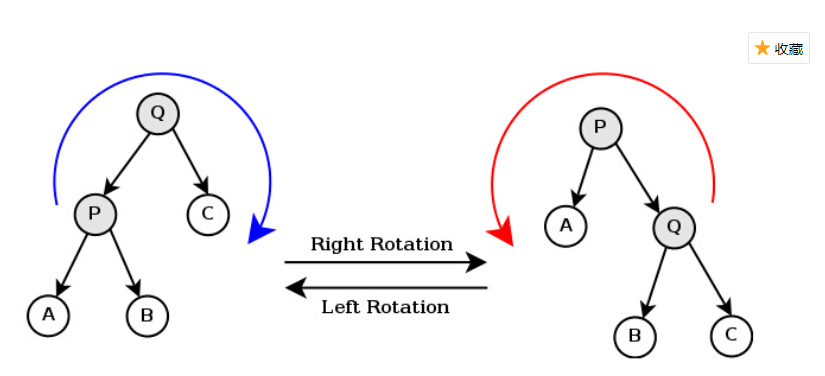
右旋的三步
1.使树根的左孩子元素成为新的根元素
2.使原根元素成为这个新树根的右孩子元素
3.使原树根的左孩子的右孩子，成为原树根的新的左孩子

• 左旋：左旋可以解决树根右孩子的右子树中较长的路径而导致的不平衡

• 右左旋：对于树根右孩子的左子树较长路径不平衡，让树根右孩子的左孩子绕树根右孩子进行一次右旋，再让所得树根右孩子绕着树根进行一次左旋

• 左右旋

• 11.5 实现二叉查找树：AVL树

  • 自树根而下的路径最大长度必须不超过log2n而且自树根而下的路径长度必须不小于log2n- 平衡因子：右子树的高度减去左子树的高度。如果平衡因子大于1或者小于-1则认为以该结点为树根的子树需要重新平衡
  • 树只有两种途径变得不平衡：插入结点或删除结点
  • 此图给出了各种旋转的示意
    
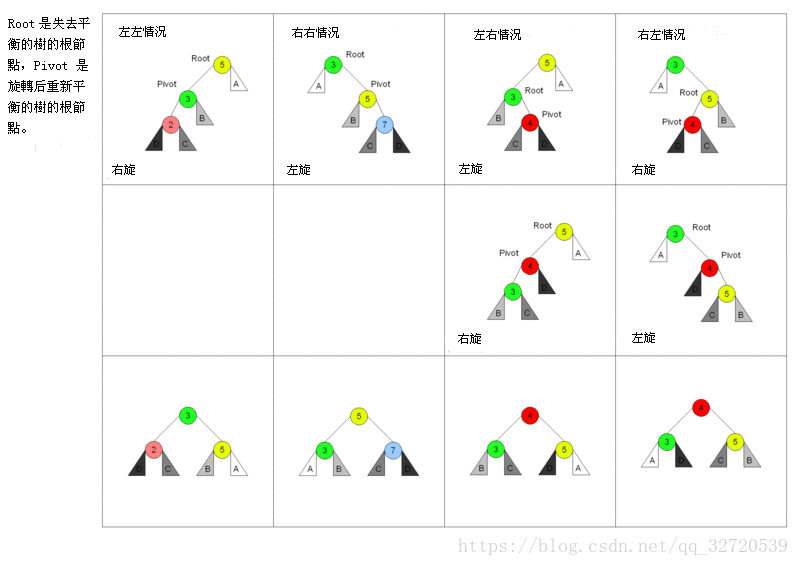
  • AVL树的右旋、左旋、右左旋、左右旋

• 11.6 实现二叉查找树：红黑树

  • 每个结点存储一种颜色，通常用一个布尔值来实现，值false等价于红色
  • 规则如下

   根结点为黑色              
   红色结点的所有孩子为黑色                 
   从树根到树叶的每条路径都包含同样数目的黑色结点              

• 在某种程度上，红黑树的平衡限制没有AVL树那么严格，但是，它们的序仍然是logn。
• 路径中至多有一半是红色结点，至少有一半是黑色结点。由此可得出红黑树的最大高度约为2logn。
• 红黑树中的元素插入
  • 元素插入之后要满足红黑树的平衡规则，所以要对树进行重新着色
  • 因为需要满足从树根到树叶的每条路径都包含同样数目的黑色结点，所以在着色的过程中要考虑到当前结点的兄弟结点的颜色情况。
  • 根据被插入节点的父结点的情况，可以将"当节点z被着色为红色结点，并插入二叉树"划分为三种情况来处理。

  ① 情况说明：被插入的结点是根结点。
    处理方法：直接把此结点涂为黑色。
  ② 情况说明：被插入的结点的父结点是黑色。
    处理方法：什么也不需要做。结点被插入后，仍然是红黑树。
  ③ 情况说明：被插入的结点的父结点是红色。
    处理方法：那么，该情况与红黑树的特性“从一个结点到该结点的子孙结点的所有路径上包含相同数目的黑结点。”相冲突。这种情况下，被插入结点是一定存在非空祖父结点的；进一步的讲，被插入结点也一定存在叔叔结点(即使叔叔结点为空，我们也视之为存在，空结点本身就是黑色结点)。理解这点之后，我们依据"叔叔结点的情况"，将这种情况进一步划分为3种情况(Case)。

/	现象说明	处理策略
case1	当前结点的父结点是红色，且当前结点的祖父结点的另一个子结点（叔叔结点）也是红色。	(01) 将“父结点”设为黑色。(02) 将“叔叔结点”设为黑色。(03) 将“祖父结点”设为“红色”。(04) 将“祖父结点”设为“当前结点”(红色结点)；即，之后继续对“当前结点”进行操作。
case2	当前结点的父结点是红色，叔叔结点是黑色，且当前结点是其父结点的右孩子	(01) 将“父结点”作为“新的当前结点”。(02) 以“新的当前结点”为支点进行左旋。
case3	当前结点的父结点是红色，叔叔结点是黑色，且当前结点是其父结点的左孩子	(01) 将“父结点”设为“黑色”。(02) 将“祖父结点”设为“红色”。(03) 以“祖父结点”为支点进行右旋。

• 以上插入情况的分类是在网上查找到的资料中给出的，教材上给出的红黑树的元素插入的分类似乎是有问题的，因为我始终无法理解为何要判断当前结点的父结点为左孩子和右孩子，且为右孩子时为何要根据兄弟结点的颜色情况分两种讨论，而为左孩子时又不再需要讨论了。
• 重新理了一遍教材内容才发现好像左右孩子的情况都有分清楚。
  手写整理--当父亲颜色为红色且父亲是右孩子时
  

当父亲是左孩子的时候

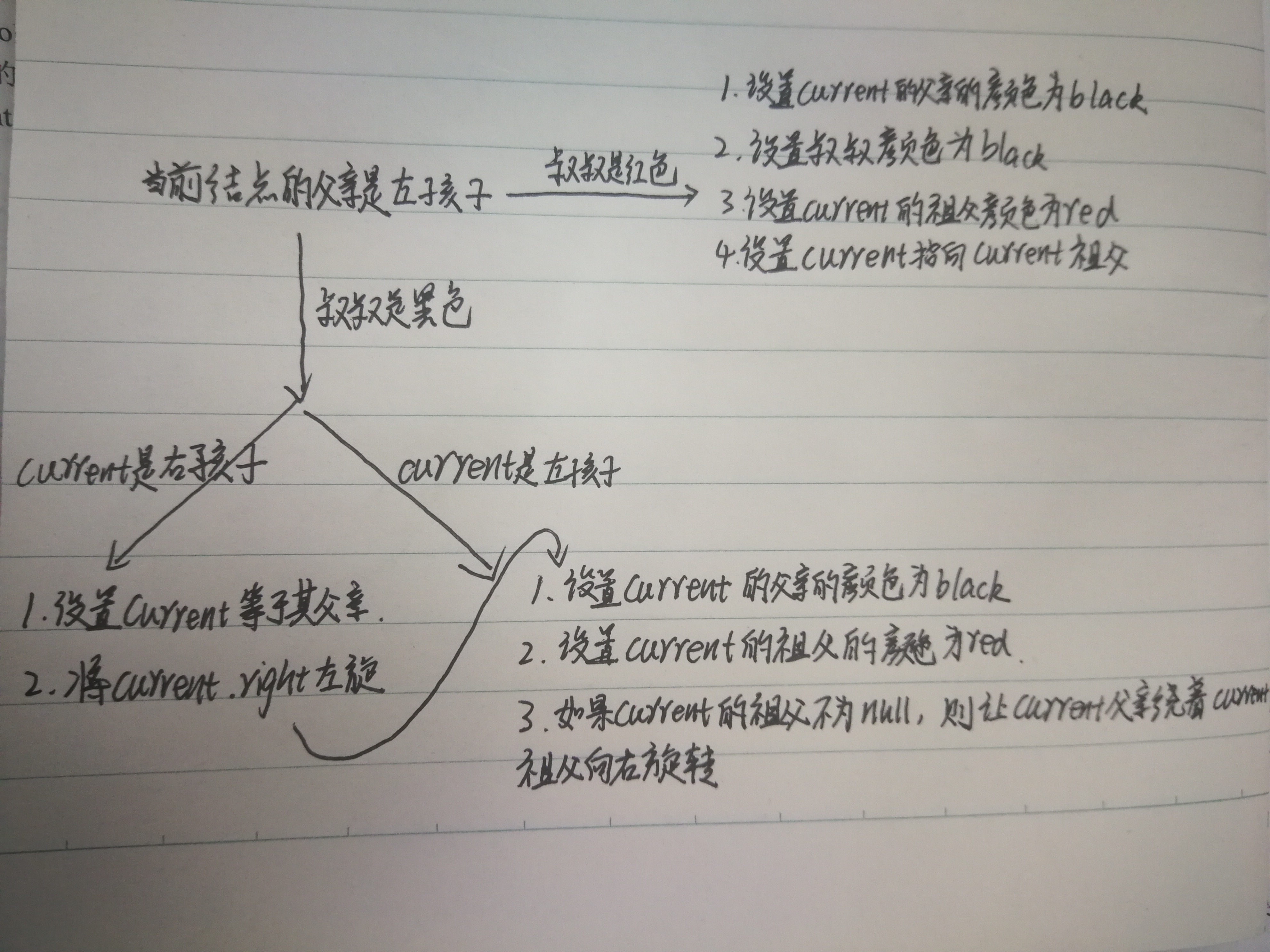
两种运行是对称的

• 红黑树中的元素删除
  • 红黑树元素删除之后的重新平衡化这一过程的终止条件是(current == root)或者(current.color == red).
  • 插入时依然要关注当前结点的父亲的兄弟的颜色
  • 如果叔叔的颜色是red

   设置叔叔的颜色为black    
   设置current的父亲颜色为red        
   让叔叔绕着current的父亲向右旋转          
   设置叔叔等于current父亲的左孩子           
   如果叔叔的两个孩子都是black或者null则需要设置叔叔的颜色为red，设置current等于current的父亲
   如果叔叔的两个孩子不全为black，如果叔叔的左孩子是black，则设置右孩子也为black，设置叔叔的颜色为red，再让兄弟的右孩子绕着兄弟本身向右旋转，最后设置叔叔等于current父亲的左孩子
   如果叔叔的两个孩子都不为black，则设置叔叔的颜色为current父亲的颜色，设置current父亲的颜色为black，设置叔叔的左孩子的颜色为black，让叔叔绕着current的父亲向右旋转，设置current等于树根。
   循环终止后删除该结点，设置其父亲的孩子引用为null

教材学习中的问题和解决过程

• 问题1：测试教材代码LinkedBinarySearchTree类的find方法时，当找不到目标元素时，系统会抛出一个错误来（如图），如何让它报错之后跟着运行接下来的程序
  
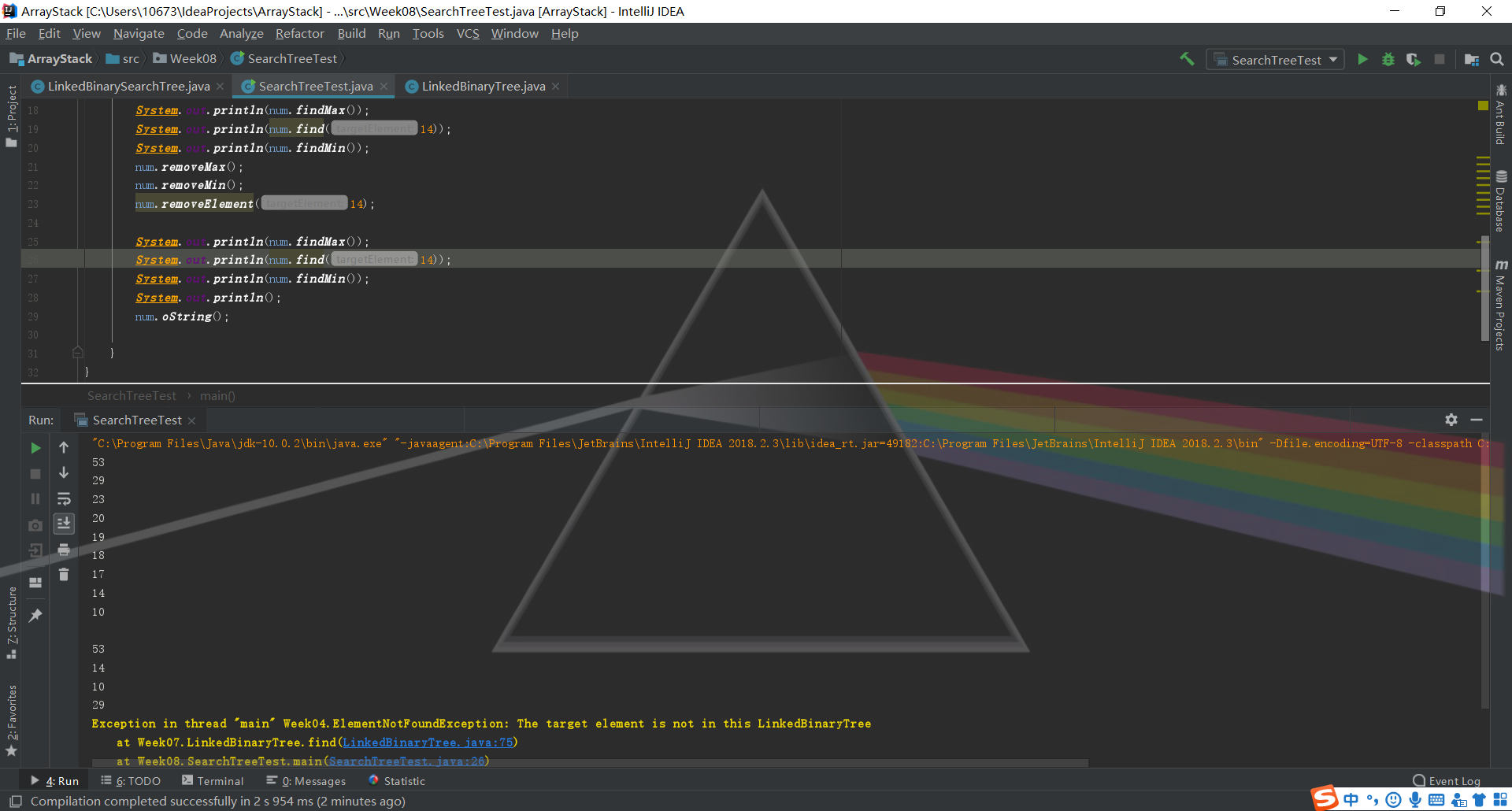
  如果程序完全不处理异常，那么该程序将会(非正常)终止并给出一条消息来描述发生的是什么异常以及发生在程序的什么地方。但此处已经对异常给出了一个解决

if (current == null)
                throw new ElementNotFoundException("LinkedBinaryTree");

为什么还是会出现这样的问题？

• 问题1解决方案:问题出错的地方好像和我想的可能出现问题的地方差别有些大，甚至可以说问题的解决是我误打误撞从而解决的，只需要简单地将throw修改为return就可以处理异常并且继续执行下去。原理是什么？
  最基本的抛出异常的知识忘得一干二净，这里的if语句其实严格上算不上捕捉异常，因为try-catch语句都没能用上，只能说是列举了一种情况当current==null时，return一个值，如果在这里用上throw语句，那么执行到这步时，他将会立即终止程序，并返回一个错误值，而return就和之后的return等同了，只不过是返回的东西不太一样罢了。

---

• 问题2：红黑树的重新平衡化过程是一种迭代过程，迭代过程的终止条件有两个，一是current == root，二是current.parent.color == black是如何执行的，同时按照书上的图示，红黑树平衡之后，树的结构似乎没有发生改变，那么是在什么地方实现了平衡？
• 问题2解决方案：首先，红黑树的插入方法类似于之前的addElement方法，所以就按照之前给出的添加方法，小于根元素往左子树的方向添加，大于或等于根元素就往右子树的方向添加，但是添加元素之后可能造成之前出现过的一些情况--某一边的子树的深度会远大于另一边子树的深度，即平衡因子会大于1或者小于-1，那么这里为什么就不需要再用左旋右旋的方法了呢？翻回11.4平衡二叉查找树提出的问题，为什么要平衡二叉查找树，是因为要防止其效率比线性结构还要低，其主要思想就是要使得各种对二叉查找树的操作的时间复杂度要保持在O(logn)而不是和线性结构一样的O(n)。AVL树提供的方法就是改变树的原有结构使之重新平衡，而红黑树提供的是另一种平衡方法，不是靠改变树的结构完成的。红黑树控制结点颜色有三个规则，上面已经给出。因为每一条路径中至多有一半结点是红色结点，至少有一半结点是黑色结点，所以从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。所以进行查找、添加、删除等操作时，遍历树时的最长路径仍然是logn。
  红黑树的迭代过程是对红黑树的重新着色，而且着色是从插入点上溯到树根的，所以迭代终止的第一种条件就是当current判断为树根时，迭代终止，将树根颜色重新定义为黑色后整个红黑树的重新着色完成。第二种条件的意思是，新插入的结点设置成为红色，如果它的父结点已经是黑色的了，那么意味着整个红黑树已经是符合规则的，不需要再进行重新的着色。

---

• 问题3：就查找而言，红黑树的查找依然是要遍历每一个元素，但在蜕化树的情况下红黑树进行查找的时间复杂度似乎依然是O(n)，它是如何解决蜕化树问题的？
• 问题3解决方案：这里犯了先入为主的错误，因为在红黑树的插入规则下，整数列表“3 5 9 12 18 20”是不会形成树中蜕化树的结构的，因此遍历时也就不需要每个元素从根到叶的看一遍，时间复杂度自然不会是O(n)。
  依然是手写模拟一下整个过程
  
  结点18、20的添加操作和3、4步添加重复，所以就直接写结果了

代码调试中的问题和解决过程

• 问题1：PP11.8在二叉树的基础上完成AVL树的方法，其中关于左旋右旋等方法如何用代码实现。

• 问题1解决方案：首先是在二叉树的基础上完成，移植二叉树的各种方法。但是需要重新设置一个AVL树结点的方法，除了设置指向左孩子、右孩子的指针之外，还需要设置一个int变量存储结点所在的高度，用于实现AVL树中的平衡因子。之后写各类旋转的方法，譬如右旋

private AVLTreeNode<T> rightRightRotation(AVLTreeNode<T> k2) {
    AVLTreeNode<T> k1;

    k1 = k2.left;
    k2.left = k1.right;
    k1.right = k2;

    k2.height = max( height(k2.left), height(k2.right)) + 1;
    k1.height = max( height(k1.left), k2.height) + 1;

    return k1;
}

如图，该树不平衡时，将整个左子树绕着k2点进行旋转，k1是k2的左孩子，于是k1成为新的根结点，k1的右孩子成为k2的左孩子，k2设置为k1的右孩子。之后再重新定义k1、k2的高度，k2从左右子树中选出较长的一支作为其高度，加一是因为树的高度从0开始。k1也是从它的左右子树中取出较长一支，但这里的右子树可以直接调用k2的高度。

再分析一下右左旋的情况

private AVLTreeNode<T> leftRightSpin(AVLTreeNode<T> node) {
        node.left = rightRightSpin(node.left);

        return leftLeftSpin(node);
    }

原理即是让初始结点的右孩子的左孩子绕初始结点的右孩子进行一次右旋node.left = rightRightSpin(node.left);，再让初始结点的右孩子绕着初始结点进行一次左旋return leftLeftSpin(node);。
类似地可以写出右旋和左右旋的方法，但是什么时候调用右旋，什么时候进行左右旋的方法还没有进行定义。以添加元素为例，这里编写了一公一私两个方法

public void addElement(T key) {
        root = addElement(root, key);
    }
    private AVLTreeNode<T> addElement(AVLTreeNode<T> tree, T element) {

        if (!(element instanceof Comparable)) {
            throw new NonComparableElementException("AVLTreeNode");
        }

        if (tree == null) {
            // 新建节点
            tree = new AVLTreeNode<T>(element, null, null);
            if (tree==null) {
                throw new EmptyCollectionException("EmptyCollectionException");
            }
        } else {

            if (element.compareTo(tree.getElement()) < 0) {    // 应该将key插入到"tree的左子树"的情况
                tree.left = addElement(tree.left, element);
                // 插入节点后，若AVL树失去平衡，则进行相应的调节。
                if (height(tree.right) - height(tree.left) == -2) {//因为查到左子树，必然左侧感度大于右侧暗度
                    if (element.compareTo(tree.left.getElement()) < 0)
                        tree = leftLeftSpin(tree);
                    else
                        tree = leftRightSpin(tree);
                }
            } else if (element.compareTo(tree.getElement()) >= 0) {    // 应该将key插入到"tree的右子树"的情况
                tree.right = addElement(tree.right, element);
                // 插入节点后，若AVL树失去平衡，则进行相应的调节。
                if (height(tree.left) - height(tree.right) == -2) {
                    if (element.compareTo(tree.right.getElement()) > 0)
                        tree = rightRightSpin(tree);
                    else
                        tree = rightLeftSpin(tree);
                }
            }
        }

        tree.height = Math.max( height(tree.left), height(tree.right)) + 1;

        return tree;
    }

最后打印树的方法调用了EXpressionTree的PrintTree方法，结果如下

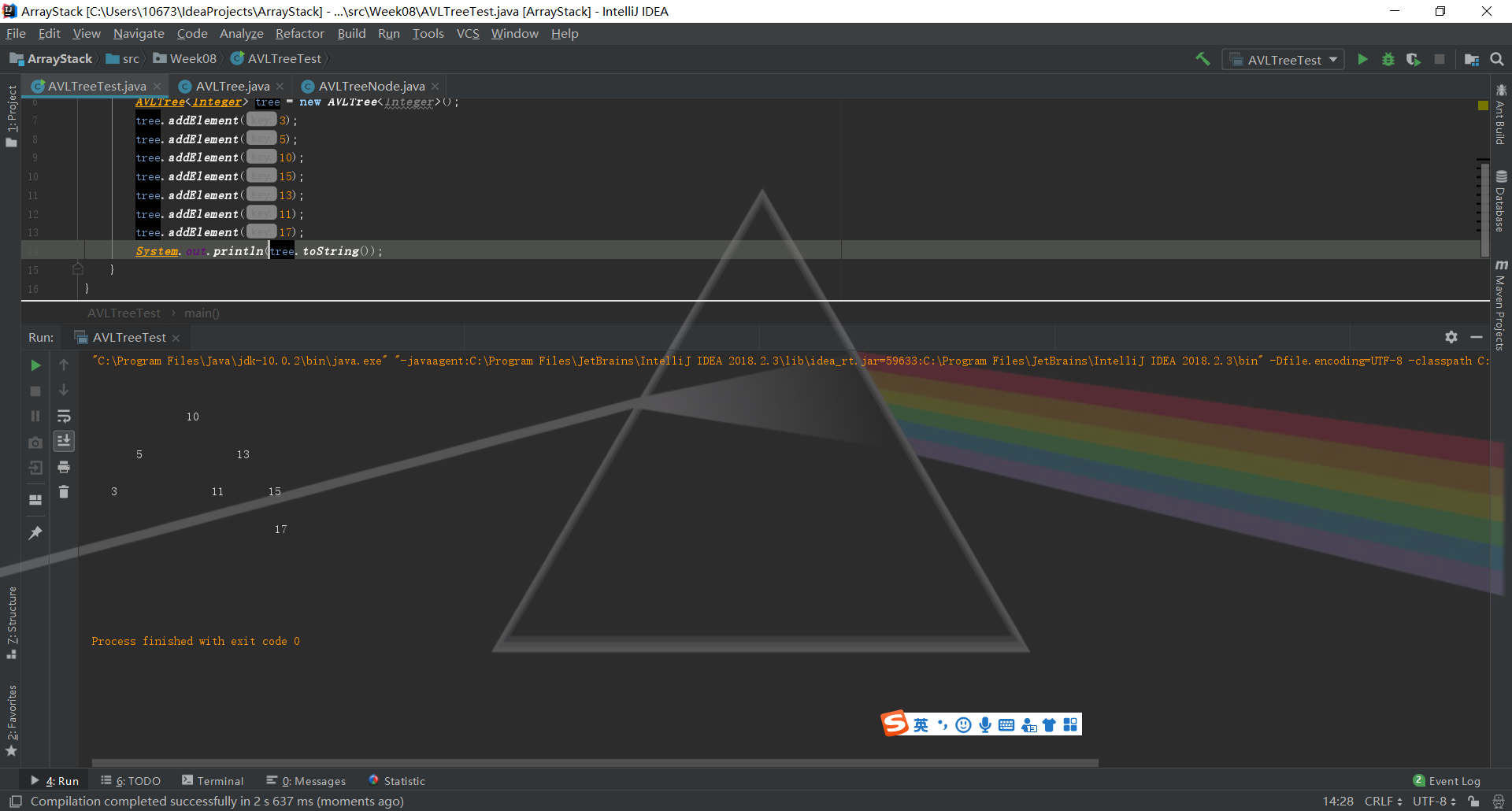
代码托管

上周考试错题总结

上周的测试似乎都是错在没有看清楚单词-_-||

中文	英文
前序遍历	preorder traversal
中序遍历	inorder traversal
后序遍历	postorder traversal
层序遍历	level-order traversal

结对及互评

• 博客中值得学习的或问题：

  • 谭鑫这周的博客感觉写的没前几周好了，不知道是不是飘了。不过呢，他记录的代码问题“在无返回值的条件下语句有return的作用？”倒是对我很有帮助
  • 方艺雯的博客记录的很详细同时很清晰，相比较而言我的博客东西一多就显得杂乱无章了

• 基于评分标准，我给谭鑫的博客打分：8分。得分情况如下：
  正确使用Markdown语法（加1分）：
  模板中的要素齐全（加1分）
  教材学习中的问题和解决过程, 一个问题加1分
  代码调试中的问题和解决过程, 五个问题加5分

• 基于评分标准，我给方艺雯的博客打分：6分。得分情况如下：、
  正确使用Markdown语法（加1分）：
  模板中的要素齐全（加1分）
  教材学习中的问题和解决过程, 三个问题加3分
  代码调试中的问题和解决过程, 一个问题加1分

• 本周结对学习情况

  • 20172305
  • 20172314
  • 结对学习内容
    • 二叉查找树

• 上周博客互评情况

  • 20172305
  • 20172314

其他

教材学习在红黑树这个地方卡了壳，前思后想冥思苦想地看教材上的讲解，一边写博客一边想一边提出疑问，导致写了一大堆啰嗦话，可是最终也没有理得太顺，也不知道我挑的教材上出现的错误是不是只是我没有理解到他真正的意图。

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	0/0	1/1	8/8
第二周	470/470	1/2	12/20
第三周	685/1155	2/4	10/30
第四周	2499/3654	2/6	12/42
第六周	1218/4872	2/8	10/52
第七周	590/5462	1/9	12/64
第八周	993/6455	1/10	12/76

参考资料

• 蓝墨云班课
• 红黑树(一)之 原理和算法详细介绍
• AVL树(三)之 Java的实现