BZOJ 1193 [HNOI2006]马步距离：大范围贪心 小范围暴搜

题目链接：http://www.lydsy.com/JudgeOnline/problem.php?id=1193

题意：

　　给定起点(px,py)、终点(sx,sy)。（x,y < 10000000）

　　每一步只能走“日”字（象棋中的马走日），坐标可以为负。

　　问你从起点到终点最少走多少步。

 

题解：

　　简化问题：

　　　　（1）从(px,py)到(sx,sy)等价于：从(abs(px-sx), abs(py-sy))到(0,0)。

　　　　（2）从(x,y)到(0,0)等价于：从(y,x)到(0,0)。

　　　　所以原题简化成：从(abs(px-sx), abs(py-sy))到(0,0)，并且可以随时交换x,y以保证x > y。

 

　　大范围贪心：

　　　　为了方便起见，始终保证x > y。

　　　　那么对于任意一个数据的最短路径都可以等价为如下形式：

　　　　

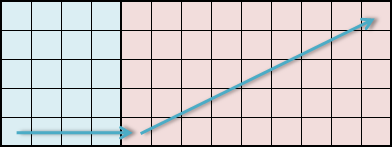
　　　　左边部分直走（先右下，再右上），右边部分往右上方走，直到接近终点时停止贪心(x+y <= 50)。

　　　　同时为了保证没有过多的直走（直走会浪费2个距离），设定直走的前提为：

　　　　　　右边区域的长宽x,y满足：((x-4)/y) > 2

　　　　　　也就是：x-4 > y*2

　　　　每直走一次，ans+=2。往右上走一次，ans++。

 

　　小范围暴搜：

　　　　bfs.

　　　　很好写，不说了。。。

　　　　注意：为了不偏离终点太远，限定可继续搜索的点要满足：abs(nx)<=100 && abs(ny)<=100

 

AC Code:

  1 #include <iostream>
  2 #include <stdio.h>
  3 #include <string.h>
  4 #include <stdlib.h>
  5 #include <queue>
  6 #define MAX_R 105
  7 
  8 using namespace std;
  9 
 10 const int dx[]={1,2,1,2,-1,-2,-1,-2};
 11 const int dy[]={2,1,-2,-1,2,1,-2,-1};
 12 
 13 struct Coor
 14 {
 15     int x;
 16     int y;
 17     Coor(int _x,int _y)
 18     {
 19         x=_x;
 20         y=_y;
 21     }
 22     Coor(){}
 23 };
 24 
 25 int x,y;
 26 int px,py;
 27 int sx,sy;
 28 int ans=0;
 29 int dis[MAX_R][MAX_R];
 30 bool vis[MAX_R][MAX_R];
 31 queue<Coor> q;
 32 
 33 void read()
 34 {
 35     cin>>px>>py>>sx>>sy;
 36     x=abs(px-sx);
 37     y=abs(py-sy);
 38 }
 39 
 40 Coor get_front()
 41 {
 42     Coor now=q.front();
 43     q.pop();
 44     return now;
 45 }
 46 
 47 void insert(Coor now)
 48 {
 49     if(vis[now.x][now.y]) return;
 50     q.push(now);
 51     vis[now.x][now.y]=true;
 52 }
 53 
 54 void bfs()
 55 {
 56     memset(dis,-1,sizeof(dis));
 57     dis[x][y]=0;
 58     insert(Coor(x,y));
 59     while(!q.empty())
 60     {
 61         Coor now=get_front();
 62         int nx=now.x;
 63         int ny=now.y;
 64         if(nx==0 && ny==0) return;
 65         if(abs(nx)>100 || abs(ny)>100) continue;
 66         for(int i=0;i<8;i++)
 67         {
 68             int tx=nx+dx[i];
 69             int ty=ny+dy[i];
 70             if(dis[tx][ty]==-1)
 71             {
 72                 dis[tx][ty]=dis[nx][ny]+1;
 73                 insert(Coor(tx,ty));
 74             }
 75         }
 76     }
 77 }
 78 
 79 void solve()
 80 {
 81     while(x+y>50)
 82     {
 83         if(x<y) swap(x,y);
 84         if(x-4>y*2)
 85         {
 86             x-=4;
 87             ans+=2;
 88         }
 89         else
 90         {
 91             x-=2;
 92             y--;
 93             ans++;
 94         }
 95     }
 96     bfs();
 97     ans+=dis[0][0];
 98 }
 99 
100 void print()
101 {
102     cout<<ans<<endl;
103 }
104 
105 int main()
106 {
107     read();
108     solve();
109     print();
110 }

 

posted @ 2017-09-05 23:43  Leohh  阅读(142)  评论(0)  编辑  收藏  举报