贝叶斯平滑方法及其代码实现
1. 背景介绍
2. 数据的层级结构
我们假设事件的发生并不是相互独立的，相反，在层级结构中相对比较靠近的两个事件的相关性要大于距离较远的两个事件，它们之间拥有很多共通之处。于是，我们便可以利用“相似”事件的信息来丰富某个我们感兴趣的事件（这个事件本事的发生的次数比较少）。具体到我们现有的场景下，可以利用与我们需要预估的事件（比如query-ad pair，或者page-ad pair）的“相似”事件的信息来帮助我们来做出预估计算。
假设有相同account下的N个ad
，以及所在的page，我们感兴趣的是page-ad pair的CTR，于是我们可以利用贝叶斯的方法来结合（1）这个ad本身的信息，以及（2）该page下与这个ad来自相同account的其它ad的信息。我们观测到的点击信息为
，这些点击信息源自各个ad的隐含CTR信息
，点击信息服从二项分布
。而隐含的每个ad的CTR，可以看做是来自于它们相同的account的公有信息，其服从贝塔分布
。于是乎，每个ad的隐含CTR值，不仅与观测到的展示点击数据
有关，还与其所属的account的整体信息有关，即与
这对超参数有关。我们可以利用二项分布和贝塔分布的共轭特性，计算所有ad所属的相同account的似然函数，然后利用最大似然估计（MLE）来计算超参数。当有了的估计值
后，我们便可以得到每个ad的后验估计：
。这个后验估计值可以作为一个平滑后的CTR值，它要比单纯地统计CTR
拥有更小的方差，更加稳定。
3. 数据的连续性
在很多场景下，我们更关心CTR的趋势，而不是一个特定时间点的CTR值。因为对于展示量较少的page-ad pair，某个特定时间点的CTR预估值是包含很大噪声的。我们将展现和点击看做是离散集合的重复观测值，然后使用指数平滑技术进行CTR平滑。
假设对于page-ad pair，我们有M天的展现
和点击
，然后我们希望预估出第M天的CTR。我们将平滑后的展现和点击记为
，它们可由下面公式得到（这里只给出了点击的公式计算，展现也同理）：
其中，
是平滑系数，它控制着我们把历史信息纳入我们平滑的计算中的权重大小。
上述的两种方法：（1）数据层级结构的贝叶斯平滑，（2）时间窗口的指数平滑，可以结合使用。
4. 数据层级结构的贝叶斯平滑方法具体介绍
这里我们规定将page-ad pair的信息在层级结构上上升到publisher-account pair的信息（不同page隶属于相同的publisher，不同的ad隶属于相同的account）。
有两个假设：
（1）对于publisher-account pair，有1个隐含的CTR概率分布，而每个page-ad pair的CTR可以看作是从这个整体的CTR分布中随机采样出来的。
（2）对于page-ad pair，我们观测到其对应的展现信息和点击信息。
其对应的概率图模型如下，灰色部分是观测变量，白色部分是隐含变量：
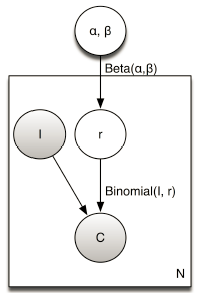
对于该publisher-account下的所有page-ad pair的点击计算出似然函数：
将上述的log似然函数分别对α和β求导数，即为：
通过fixed-point iteration方法，我们可以得到α和β在每一轮迭代中的更新公式：
迭代的终止条件为一个固定的迭代次数（如1000次），或者α和β在一次迭代中的变化值都小于一个epsilon（如1E-10）。一旦有了的估计值后，我们便可以得到每个ad的后验估计：。
5. 参数估计的几种方法
1. 矩估计
矩估计在这里是相对比较简单的参数估计方法。矩估计的方法要追溯到19世纪的Karl Pearson，是基于一种简单的 “替换” 思想建立起来的一种估计方法。 其基本思想是用样本矩估计总体矩. 由大数定理，如果未知参数和总体的某个(些)矩有关系，我们可以很自然地来构造未知参数的估计。具体计算步骤如下：
1）根据给出的概率密度函数，计算总体的原点矩（如果只有一个参数只要计算一阶原点矩，如果有两个参数要计算一阶和二阶）。由于有参数这里得到的都是带有参数的式子。比如，有两个参数时，需要先计算出：期望
; 方差 
2）根据给出的样本，按照计算样本的原点矩。通常它的均值用 
表示，方差用 
表示。（另外提一句，求时，通常用n-1为底。这样是想让结果跟接近总体的方差，又称为无偏估计。）
3）让总体的原点矩与样本的原点矩相等，解出参数。所得结果即为参数的矩估计值。
2. fixed-point iteration
首先构造出似然函数，然后利用fixed-point iteration来求得似然函数的最大值。
1）首先给出参数的一个初始值。
2）在初始值处，构造似然函数的一个紧的下界函数。这个下界函数可以用closed-form的方式计算其最大值处的参数值，将此参数值作为新的参数估计。
3）不断重复上述（2）的步骤，直至收敛。此时便可到达似然函数的stationary point。
其实fixed-point iteration（不动点迭代）的思想与EM类似。
3. EM
通过将概率参数作为隐含变量，任何估计概率参数的算法都可以进一步变成估计个数参数的算法。
（1）E-step：计算出p在已观测数据（观测到的每个类别发生的次数，以及每个类别的超参数值的上一轮迭代的取值）下的后验分布，便可以得到complete data的对数似然函数的期望值。
（2）M-step：对E-step中的期望值求最大值，便可得到相应的超参数的本轮迭代的更新值。
（3）不断重复地运行E-step和M-step，直至收敛。
6. 数据层级结构的贝叶斯平滑方法代码实现
#!/usr/bin/python
# coding=utf-8
import numpy
import random
import scipy.special as special
class BayesianSmoothing(object):
def __init__(self, alpha, beta):
self.alpha = alpha
self.beta = beta
def sample(self, alpha, beta, num, imp_upperbound):
sample = numpy.random.beta(alpha, beta, num)
I = []
C = []
for clk_rt in sample:
imp = random.random() * imp_upperbound
imp = imp_upperbound
clk = imp * clk_rt
I.append(imp)
C.append(clk)
return I, C
def update(self, imps, clks, iter_num, epsilon):
for i in range(iter_num):
new_alpha, new_beta = self.__fixed_point_iteration(imps, clks, self.alpha, self.beta)
if abs(new_alpha-self.alpha)<epsilon and abs(new_beta-self.beta)<epsilon:
break
self.alpha = new_alpha
self.beta = new_beta
def __fixed_point_iteration(self, imps, clks, alpha, beta):
numerator_alpha = 0.0
numerator_beta = 0.0
denominator = 0.0
for i in range(len(imps)):
numerator_alpha += (special.digamma(clks[i]+alpha) - special.digamma(alpha))
numerator_beta += (special.digamma(imps[i]-clks[i]+beta) - special.digamma(beta))
denominator += (special.digamma(imps[i]+alpha+beta) - special.digamma(alpha+beta))
return alpha*(numerator_alpha/denominator), beta*(numerator_beta/denominator)
def test():
bs = BayesianSmoothing(1, 1)
I, C = bs.sample(500, 500, 1000, 10000)
print I, C
bs.update(I, C, 1000, 0.0000000001)
print bs.alpha, bs.beta
if __name__ == '__main__':
test()
7. 参考文献
1. Click-Through Rate Estimation for Rare Events in Online Advertising
版权声明：
本文由笨兔勿应所有，发布于http://www.cnblogs.com/bentuwuying。如果转载，请注明出处，在未经作者同意下将本文用于商业用途，将追究其法律责任。
