外部排序&多路归并排序
外部排序:
一、定义问题
外部排序指的是大文件的排序,即待排序的记录存储在外存储器上,待排序的文件无法一次装入内存,需要在内存和外部存储器之间进行多次数据交换,以达到排序 整个文件的目的。外部排序最常用的算法是多路归并排序,即将原文件分解成多个能够一次性装入内存的部分,分别把每一部分调入内存完成排序。然后,对已经排 序的子文件进行多路归并排序。
二、处理过程
(1)按可用内存的大小,把外存上含有n个记录的文件分成若干个长度为L的子文件,把这些子文件依次读入内存,并利用有效的内部排序方法对它们进行排序,再将排序后得到的有序子文件重新写入外存;
(2)对这些有序子文件逐趟归并,使其逐渐由小到大,直至得到整个有序文件为止。
先从一个例子来看外排序中的归并是如何进行的?
假设有一个含10000 个记录的文件,首先通过10 次内部排序得到10 个初始归并段R1~R10 ,其中每一段都含1000 个记录。然后对它们作如图10.11 所示的两两归并,直至得到一个有序文件为止 如下图

三 、多路归并排序算法以及败者树
多路归并排序算法在常见数据结构书中都有涉及。从2路到多路(k路),增大k可以减少外存信息读写时间,但k个归并段中选取最小的记录需要比较k-1次, 为得到u个记录的一个有序段共需要(u-1)(k-1)次,若归并趟数为s次,那么对n个记录的文件进行外排时,内部归并过程中进行的总的比较次数为 s(n-1)(k-1),也即(向上取整)(logkm)(k-1)(n-1)=(向上取整)(log2m/log2k)(k-1)(n-1),而(k- 1)/log2k随k增而增因此内部归并时间随k增长而增长了,抵消了外存读写减少的时间,这样做不行,由此引出了“败者树”tree of loser的使用。在内部归并过程中利用败者树将k个归并段中选取最小记录比较的次数降为(向上取整)(log2k)次使总比较次数为(向上取整) (log2m)(n-1),与k无关。
败者树是完全二叉树, 因此数据结构可以采用一维数组。其元素个数为k个叶子结点、k-1个比较结点、1个冠军结点共2k个。ls[0]为冠军结点,ls[1]--ls[k- 1]为比较结点,ls[k]--ls[2k-1]为叶子结点(同时用另外一个指针索引b[0]--b[k-1]指向)。另外bk为一个附加的辅助空间,不 属于败者树,初始化时存着MINKEY的值。
多路归并排序算法的过程大致为:
1):首先将k个归并段中的首元素关键字依次存入b[0]--b[k-1]的叶子结点空间里,然后调用CreateLoserTree创建败者树,创建完毕之后最小的关键字下标(即所在归并段的序号)便被存入ls[0]中。然后不断循环:
2)把ls[0]所存最小关键字来自于哪个归并段的序号得到为q,将该归并段的首元素输出到有序归并段里,然后把下一个元素关键字放入上一个元素本来所 在的叶子结点b[q]中,调用Adjust顺着b[q]这个叶子结点往上调整败者树直到新的最小的关键字被选出来,其下标同样存在ls[0]中。循环这个 操作过程直至所有元素被写到有序归并段里。
外部排序之多路归并
该外部排序上场了.
外部排序干嘛的?
- 内存极少的情况下,利用分治策略,利用外存保存中间结果,再用多路归并来排序;
- map-reduce的嫡系.
1.分
内存中维护一个极小的核心缓冲区bigdata按行读入,搜集到memBuffer中的数据调用内排进行排序,排序后将有序结果写入磁盘文件
循环利用
2.合
现在有了n个有序的小文件,怎么合并成1个有序的大文件?
把所有小文件读入内存,然后内排?
(⊙o⊙)…
no!
利用如下原理进行归并排序:
我们举个简单的例子:
文件1:3,6,9
文件2:2,4,8
文件3:1,5,7第一回合:
文件1的最小值:3 , 排在文件1的第1行
文件2的最小值:2,排在文件2的第1行
文件3的最小值:1,排在文件3的第1行
那么,这3个文件中的最小值是:min(1,2,3) = 1
也就是说,最终大文件的当前最小值,是文件1、2、3的当前最小值的最小值,绕么?
上面拿出了最小值1,写入大文件.
第二回合:
文件1的最小值:3 , 排在文件1的第1行
文件2的最小值:2,排在文件2的第1行
文件3的最小值:5,排在文件3的第2行
那么,这3个文件中的最小值是:min(5,2,3) = 2
将2写入大文件.也就是说,最小值属于哪个文件,那么就从哪个文件当中取下一行数据.(因为小文件内部有序,下一行数据代表了它当前的最小值)
败者树可以改善时间复杂度:
胜者树与败者树
胜者树和败者树都是完全二叉树,是树形选择排序的一种变型。每个叶子结点相当于一个选手,每个中间结点相当于一场比赛,每一层相当于一轮比赛。
不同的是,胜者树的中间结点记录的是胜者的标号;而败者树的中间结点记录的败者的标号。
胜者树与败者树可以在log(n)的时间内找到最值。任何一个叶子结点的值改变后,利用中间结点的信息,还是能够快速地找到最值。在k路归并排序中经常用到。
一、胜者树
胜者树的一个优点是,如果一个选手的值改变了,可以很容易地修改这棵胜者树。只需要沿着从该结点到根结点的路径修改这棵二叉树,而不必改变其他比赛的结果。
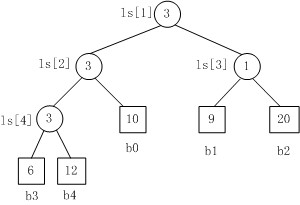
Fig. 1
Fig.1是一个胜者树的示例。规定数值小者胜。
1. b3 PK b4,b3胜b4负,内部结点ls[4]的值为3;
2. b3 PK b0,b3胜b0负,内部结点ls[2]的值为3;
3. b1 PK b2,b1胜b2负,内部结点ls[3]的值为1;
4. b3 PK b1,b3胜b1负,内部结点ls[1]的值为3。.
当Fig. 1中叶子结点b3的值变为11时,重构的胜者树如Fig. 2所示。
1. b3 PK b4,b3胜b4负,内部结点ls[4]的值为3;
2. b3 PK b0,b0胜b3负,内部结点ls[2]的值为0;
3. b1 PK b2,b1胜b2负,内部结点ls[3]的值为1;
4. b0 PK b1,b1胜b0负,内部结点ls[1]的值为1。.
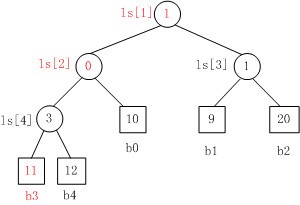
Fig. 2
二、败者树
败者树是胜者树的一种变体。在败者树中,用父结点记录其左右子结点进行比赛的败者,而让胜者参加下一轮的比赛。败者树的根结点记录的是败者,需要加一个结点来记录整个比赛的胜利者。采用败者树可以简化重构的过程。
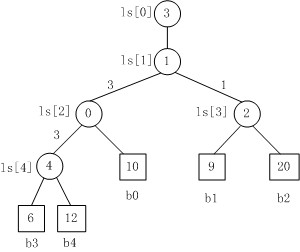
Fig. 3
Fig. 3是一棵败者树。规定数大者败。
1. b3 PK b4,b3胜b4负,内部结点ls[4]的值为4;
2. b3 PK b0,b3胜b0负,内部结点ls[2]的值为0;
3. b1 PK b2,b1胜b2负,内部结点ls[3]的值为2;
4. b3 PK b1,b3胜b1负,内部结点ls[1]的值为1;
5. 在根结点ls[1]上又加了一个结点ls[0]=3,记录的最后的胜者。
败者树重构过程如下:
· 将新进入选择树的结点与其父结点进行比赛:将败者存放在父结点中;而胜者再与上一级的父结点比较。
· 比赛沿着到根结点的路径不断进行,直到ls[1]处。把败者存放在结点ls[1]中,胜者存放在ls[0]中。
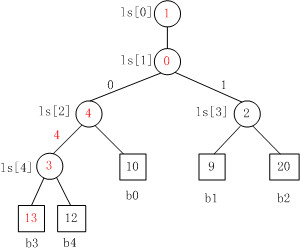
Fig. 4
Fig. 4是当b3变为13时,败者树的重构图。
注意,败者树的重构跟胜者树是不一样的,败者树的重构只需要与其父结点比较。对照Fig. 3来看,b3与结点ls[4]的原值比较,ls[4]中存放的原值是结点4,即b3与b4比较,b3负b4胜,则修改ls[4]的值为结点3。同理,以此 类推,沿着根结点不断比赛,直至结束。
由上可知,败者树简化了重构。败者树的重构只是与该结点的父结点的记录有关,而胜者树的重构还与该结点的兄弟结点有关。
二 使用败者树加快合并排序
外部排序最耗时间的操作时磁盘读写,对于有m个初始归并段,k路平衡的归并排序,磁盘读写次数为
|logkm|,可见增大k的值可以减少磁盘读写的次数,但增大k的值也会带来负面效应,即进行k路合并
的时候会增加算法复杂度,来看一个例子。
把n个整数分成k组,每组整数都已排序好,现在要把k组数据合并成1组排好序的整数,求算法复杂度
u1: xxxxxxxx
u2: xxxxxxxx
u3: xxxxxxxx
.......
uk: xxxxxxxx
算法的步骤是:每次从k个组中的首元素中选一个最小的数,加入到新组,这样每次都要比较k-1次,故
算法复杂度为O((n-1)*(k-1)),而如果使用败者树,可以在O(logk)的复杂度下得到最小的数,算法复杂
度将为O((n-1)*logk), 对于外部排序这种数据量超大的排序来说,这是一个不小的提高。



