主席树模板

　  主席树,又名函数式线段树.是fotile主席创建出来的这个数据结构,所以叫主席树.

　  然后这里有一些最常用的主席树需要解决的问题.

      在这里推荐一个巨佬的博客Brave_Cattle. 写的贼好.

　主席树_ 求区间K大值

　  题目大意：

　  给一个长为n的序列，m次询问，每次询问[l, r]内第k大的数是几.n <= 100000, m <= 5000.

　　

　  首先因为是多次离线求区间的K大值,而且又因为数据范围的限制,所以传统的线段树显然是不可行的.然后这里我们就需要用到主席树.

　  主席树,首先有几个东西需要明确.

  •  主席树内有多棵线段树, 而且利用到了类似于前缀和的思想和做法.

     

  • 主席树所用的储存数据的结构,是比较巧妙的,即就把前后一致的一些一样结点多棵线段树共用.

　  

　  由于数据原因,所以我们一般需要先将数据离散化一波.

　  然后就开始讲每一棵线段树的建立.

 

　　

　  这里引用一组数据 :

　　7 1
　　1 5 2 6 3 7 4
　　2 5 3

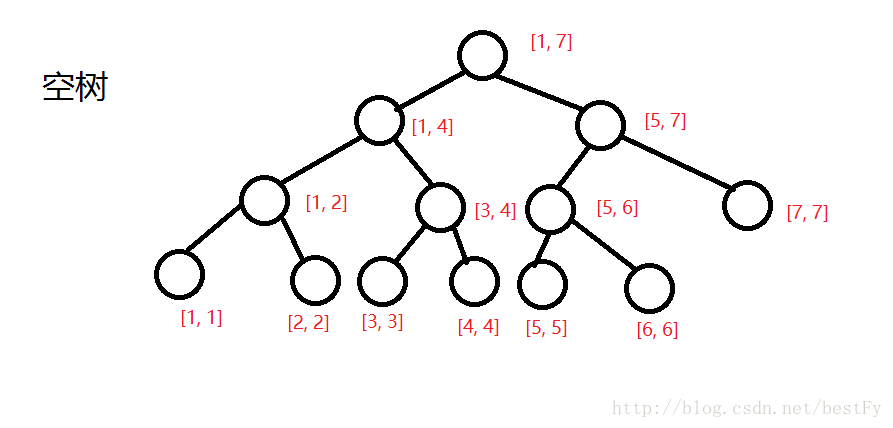
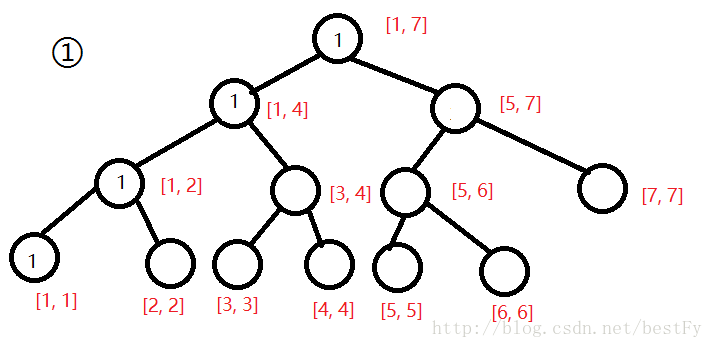
　　首先,我们需要先建一棵空树.

　　 同时,我们需要记录每一个节点的左儿子和右儿子.

　　在传统线段树中,node*2 和 node*2+1 分别为左儿子和右儿子.

　　但是主席树中不满足此性质,所以需要记录 l,r 节点.

　　同时如果需要去遍历第几棵线段树的话,直接从它的根节点开始遍历即可.

　　这里我们用 T  数组记录根.

　　

　　　

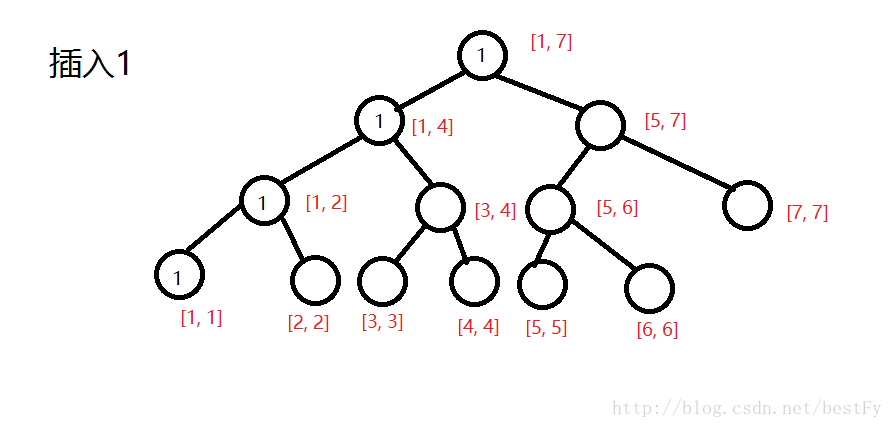
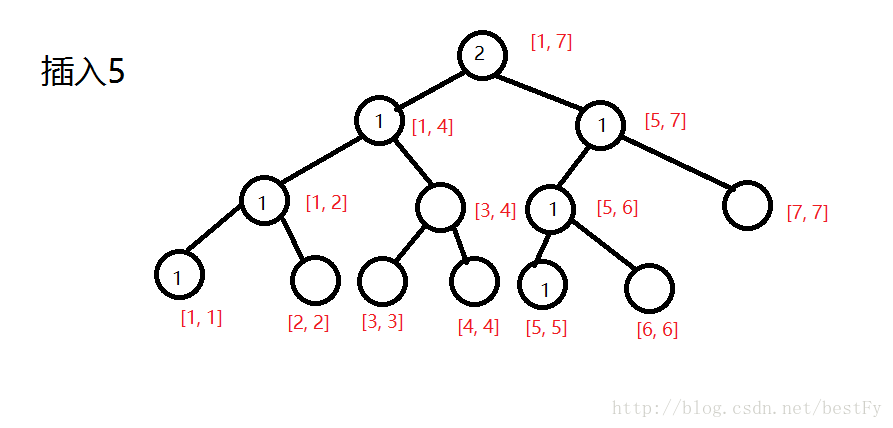
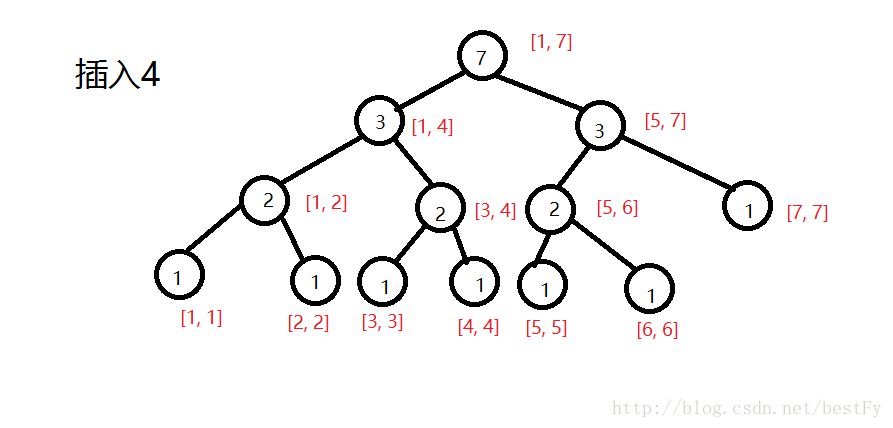
 　　　然后依次将所有的结点 按照离散化所得到的顺序将结点一个一个插进去.

　　　 在插入的时候,更新sum数组. sum数组所起的所用就是一个前缀和的作用,表示这个结点被遍历了几次.

　　　　

　　　　

　　

　　

　　　　　　　　

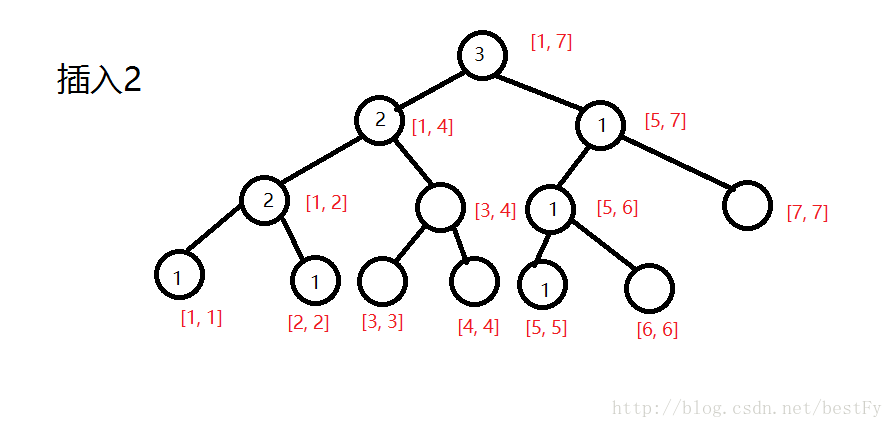
　　　　　　直到把所有数字插入以后，情况是这样的。

　　

　　　　　　

　　　　那

么建树的具体过程大致如上。接下来我们考虑查询。

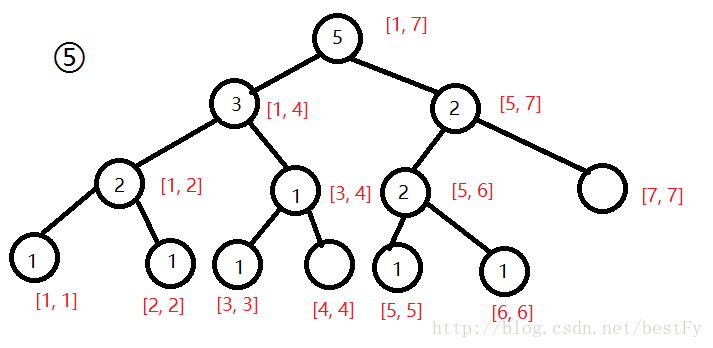
　　　　要查询[2, 5]中第3大的数我们首先把第1棵线段树和第5棵拿出来。

 

　　　　　　　　　　　　

　　　　　　　　　　　　

　　　　　然后查询就是前面说的前缀和的做法了.

　　　　　第1棵线段树和第5棵线段树,之间的差值部分就是我们所需要查询的线段树部分.

　　　　　查询的时候有类似于Splay 的做法. 即找到当前结点,看是否之前左儿子统计的前缀和是否大于k,如果大于k, 那么我们就继续递归下去.

　　　　　直到找到一个只有一个元素的结点,即为我们所需要的答案.

 

代码:　　　　　

#include<bits/stdc++.h
#define mid (l+r)/2
#define lc o<<1
#define rc o<<1|1
using namespace std;
typedef long long LL;
const int N=100010,LOG=20;
int n,m,q,tot=0;
int a[N],b[N];
int T[N],sum[N*LOG],L[N*LOG],R[N*LOG];
//T数组用于储存根节点.
//sum数组用于储存每一个点被遍历的次数.
//L,R 分别为左儿子和右儿子.
//传统线段树中满足 node*2 即为左儿子,node*2+1 即为右儿子,但主席树中并不满足
//tot 用于记录节点个数和编号.
inline int build(int l, int r)
{
    int rt=++tot;
    if (l<r)
        L[rt]=build(l,mid),
        R[rt]=build(mid+1,r);
    return rt;
}
//我们需要先建立一棵空树.
inline int update(int pre,int l,int r,int x)
{
    int rt=++tot;
    L[rt]=L[pre]; 
    R[rt]=R[pre];
    //先继承上一次插入时的左儿子以及右儿子 
    sum[rt]=sum[pre]+1;
    //因为这里被遍历了一次,所以我们要+1 
    if(l!=r)
    {
        if (x<=mid) L[rt]=update(L[pre],l,mid,x);
        else R[rt]=update(R[pre],mid+1,r,x);
        //如果说需要修改,那么此时上一次的左儿子和右儿子就不适合我们了.
        //所以我们需要将其更改.
    }
    return rt;
}
//每一次依次将排好序的序列加入主席树中.
inline int query(int u, int v, int l, int r, int k)
{
    if (l==r) return l;
    int x=sum[L[v]]-sum[L[u]];
    //查看是往左边走还是往右边走.
    if (x>=k) return query(L[u],L[v],l,mid,k);
    else return query(R[u],R[v],mid+1,r,k-x);
}
//查询时是类似于 Splay 的查询.
int x,y,z; 
int main()
{
    int Test; scanf("%d", &Test);
    while(Test--)
    {
        tot=0;
        memset(T,0,sizeof T); memset(sum,0,sizeof sum);
        memset(L,0,sizeof L); memset(R,0,sizeof R);
        scanf("%d%d",&n,&q);
        for(int i=1;i<=n;i++)
        scanf("%d",&a[i]),b[i] = a[i];
        sort(b+1,b+1+n);
        m=unique(b+1,b+1+n)-b-1;
        T[0]=build(1,m);
        for(int i=1;i<=n;i++)
            a[i]=lower_bound(b+1,b+1+m,a[i])-b,
                T[i]=update(T[i-1],1,m,a[i]);
        while (q--)
        {
            scanf("%d%d%d",&x,&y,&z);
            int p=query(T[x-1],T[y],1,m,z);
            printf("%d\n",b[p]);
        }
    }
    return 0;
}

 

　

注: 以上有一些图片转自另一博客  　　　　　

　　　　　

posted @ 2018-04-03 20:18  Kevin_naticl  阅读(1069)  评论(1)  编辑  收藏  举报