【POJ2699】The Maximum Number of Strong Kings(网络流)
Description
A tournament can be represented by a complete graph in which each vertex denotes a player and a directed edge is from vertex x to vertex y if player x beats player y. For a player x in a tournament T, the score of x is the number of players beaten by x. The score sequence of T, denoted by S(T) = (s1, s2, . . . , sn), is a non-decreasing list of the scores of all the players in T. It can be proved that S(T) = (s1, s2, . . . , sn) is a score sequence of T if and only if
for k = 1, 2, . . . , n and equality holds when k = n. A player x in a tournament is a strong king if and only if x beats all of the players whose scores are greater than the score of x. For a score sequence S, we say that a tournament T realizes S if S(T) = S. In particular, T is a heavy tournament realizing S if T has the maximum number of strong kings among all tournaments realizing S. For example, see T2 in Figure 1. Player a is a strong king since the score of player a is the largest score in the tournament. Player b is also a strong king since player b beats player a who is the only player having a score larger than player b. However, players c, d and e are not strong kings since they do not beat all of the players having larger scores.
The purpose of this problem is to find the maximum number of strong kings in a heavy tournament after a score sequence is given. For example,Figure 1 depicts two possible tournaments on five players with the same score sequence (1, 2, 2, 2, 3). We can see that there are at most two strong kings in any tournament with the score sequence (1, 2, 2, 2, 3) since the player with score 3 can be beaten by only one other player. We can also see that T2 contains two strong kings a and b. Thus, T2 is one of heavy tournaments. However, T1 is not a heavy tournament since there is only one strong king in T1. Therefore, the answer of this example is 2.
Input
The first line of the input file contains an integer m, m <= 10, which represents the number of test cases. The following m lines contain m score sequences in which each line contains a score sequence. Note that each score sequence contains at most ten scores.
Output
The maximum number of strong kings for each test case line by line.
Sample Input
5 1 2 2 2 3 1 1 3 4 4 4 4 3 3 4 4 4 4 5 6 6 6 0 3 4 4 4 5 5 5 6 0 3 3 3 3 3
Sample Output
2 4 5 3 5
【分析】
主要是有一个贪心的思想,就是如果有一种情况使其中k个人是能力者的话,那么总有一种情况使分数最高的k个人是能力者。(因为交换一下胜利的场就可以了)。所以可以枚举有k个人是能力者,规定后k个人就是能力者,建立约束图,跑最大流判满流即可。
如下图(证明上面那一个贪心):

假设有一种情况使得有k个能力者,但不是后k个,证明有一种情况是后k个都是能力者。
上图,假设C是能力者但不是后k个,E不是能力者但是后k个。
因为C是能力者E不是,则在E的后面必有一个G(随便是什么),C赢了它,E没有赢他。
因为E的分数大于C,则在C之前必有一个A(随便是什么),C没有赢他,E赢了他。
那么我们交换一下胜负场,C、E分数都不变,然后E离能力者更近一步。
继续交换下去,后k个一定能成为能力者。
证毕。
于是建个图跑最大流。
差不多这样建图:
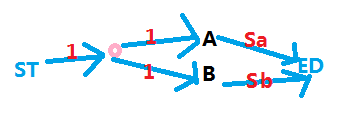
代码如下:

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 #include<queue> 7 using namespace std; 8 #define Maxn 1100 9 #define Maxm 100100 10 #define INF 0xfffffff 11 12 char s[1010]; 13 int a[Maxn],al,lg[Maxn]; 14 int dis[Maxn],first[Maxn]; 15 16 struct node 17 { 18 int x,y,f,o,next; 19 }t[Maxm];int len; 20 21 int st,ed,sum,h=0; 22 23 int mymin(int x,int y) {return x<y?x:y;} 24 25 void ins(int x,int y,int f) 26 { 27 if(f==0) return; 28 if(y==ed) sum+=f; 29 t[++len].x=x;t[len].y=y;t[len].f=f; 30 t[len].next=first[x];first[x]=len;t[len].o=len+1; 31 t[++len].x=y;t[len].y=x;t[len].f=0; 32 t[len].next=first[y];first[y]=len;t[len].o=len-1; 33 } 34 35 queue<int > q; 36 bool bfs() 37 { 38 while(!q.empty()) q.pop(); 39 memset(dis,-1,sizeof(dis)); 40 q.push(st);dis[st]=0; 41 while(!q.empty()) 42 { 43 int x=q.front();q.pop(); 44 for(int i=first[x];i;i=t[i].next) if(t[i].f>0) 45 { 46 int y=t[i].y; 47 if(dis[y]==-1) 48 { 49 dis[y]=dis[x]+1; 50 q.push(y); 51 } 52 } 53 } 54 if(dis[ed]==-1) return 0; 55 return 1; 56 } 57 58 int ffind(int x,int flow) 59 { 60 if(x==ed) return flow; 61 int now=0; 62 for(int i=first[x];i;i=t[i].next) if(t[i].f>0) 63 { 64 int y=t[i].y; 65 if(dis[y]==dis[x]+1) 66 { 67 int a=ffind(y,mymin(flow-now,t[i].f)); 68 t[i].f-=a; 69 t[t[i].o].f+=a; 70 now+=a; 71 } 72 if(now==flow) break; 73 } 74 if(now==0) dis[x]=-1; 75 return now; 76 } 77 78 bool max_flow() 79 { 80 int ans=0; 81 while(bfs()) 82 { 83 ans+=ffind(st,INF); 84 } 85 if(ans==sum) return 1; 86 return 0; 87 } 88 89 bool check(int x) 90 { 91 len=0;sum=0;h=ed; 92 memset(first,0,sizeof(first)); 93 for(int i=al-x+1;i<=al;i++) 94 { 95 if(a[i]<lg[i]) return 0; 96 ins(i,ed,a[i]-lg[i]); 97 for(int j=i+1;j<=al-lg[i];j++) 98 { 99 ins(st,++h,1); 100 ins(h,i,1); 101 ins(h,j,1); 102 } 103 } 104 for(int i=1;i<=al-x;i++) ins(i,ed,a[i]); 105 for(int i=1;i<=al-x;i++) 106 for(int j=i+1;j<=al;j++) 107 { 108 ins(st,++h,1); 109 ins(h,i,1); 110 ins(h,j,1); 111 } 112 113 if(max_flow()) return 1; 114 115 return 0; 116 } 117 118 int main() 119 { 120 int T; 121 scanf("%d",&T);getchar(); 122 while(T--) 123 { 124 gets(s); 125 int l=strlen(s); 126 int now=0;al=0; 127 for(int i=0;i<l;i++) 128 { 129 if((s[i]<='0'||s[i]>='9')&&(i>=1&&s[i-1]>='0'&&s[i-1]<='9')) 130 { 131 a[++al]=now; 132 now=0; 133 } 134 else if(s[i]>='0'&&s[i]<='9')now=now*10+s[i]-'0'; 135 } 136 if(s[l-1]>='0'&&s[l-1]<='9') a[++al]=now; 137 for(int i=1;i<=al;i++) 138 { 139 lg[i]=0; 140 for(int j=i+1;j<=al;j++) if(a[j]>a[i]) lg[i]++; 141 } 142 st=al+1;ed=st+1;h=ed; 143 int ans=0; 144 for(int i=al;i>=1;i--) 145 { 146 if(check(i)) {ans=i;break;} 147 } 148 printf("%d\n",ans); 149 } 150 return 0; 151 }
2016-06-05 10:17:08


