Luogu 3369 普通平衡树

题目描述

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

  1. 插入x数

  2. 删除x数(若有多个相同的数，因只删除一个)

  3. 查询x数的排名(排名定义为比当前数小的数的个数+1。若有多个相同的数，因输出最小的排名)

  4. 查询排名为x的数

  5. 求x的前驱(前驱定义为小于x，且最大的数)

  6. 求x的后继(后继定义为大于x，且最小的数)

输入输出格式

输入格式：

第一行为n，表示操作的个数,下面n行每行有两个数opt和x，opt表示操作的序号( 1≤opt≤6 1 \leq opt \leq 6 1≤opt≤6 )

输出格式：

对于操作3,4,5,6每行输出一个数，表示对应答案

输入输出样例

输入样例#1：
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
输出样例#1：
106465
84185
492737

说明

时空限制：1000ms,128M

1.n的数据范围： n≤100000 n \leq 100000 n≤100000

2.每个数的数据范围： [−107,107][-{10}^7, {10}^7][−10​7​​,10​7​​]

来源：Tyvj1728 原名：普通平衡树

在此鸣谢

01trie拟或成为最大赢家（虽然说空间有点那啥。。。不过时间复杂度是严格log的。。。）。。。

01trie是个神奇的东西。。。
将每个数字二进制拆分后（需要先加上1e7使得都是非负整数）从高位到地位插入到trie中（只保存01节点），然后查询的话YY一下就行（或者看代码）。
01trie十分好写！！！01trie十分好写！！！01trie十分好写！！！
如果说split-merge treap是时间换代码的话（事实上那个我觉得不太好理解。。。而且一般split用的pair速度超慢的样子。。。（不过clj的那种不需要保存优先值的方法挺好的。。。）），01trie就是空间换代码（然而只是32倍的空间！而且是最烂的情况下！）。。。
不过美中不足的是，01trie只能用于非负整数（也就是说其它的数据（比如说实数）需要先离散化后才能用。。。）。。。
（然而事实上考试的时候都是强制在线吧。。。）
不过一般写平衡树就是整数了吧。。。于是01trie还是很实用的样子。。。╰(*´︶`*)╯

（看起来的确很短）

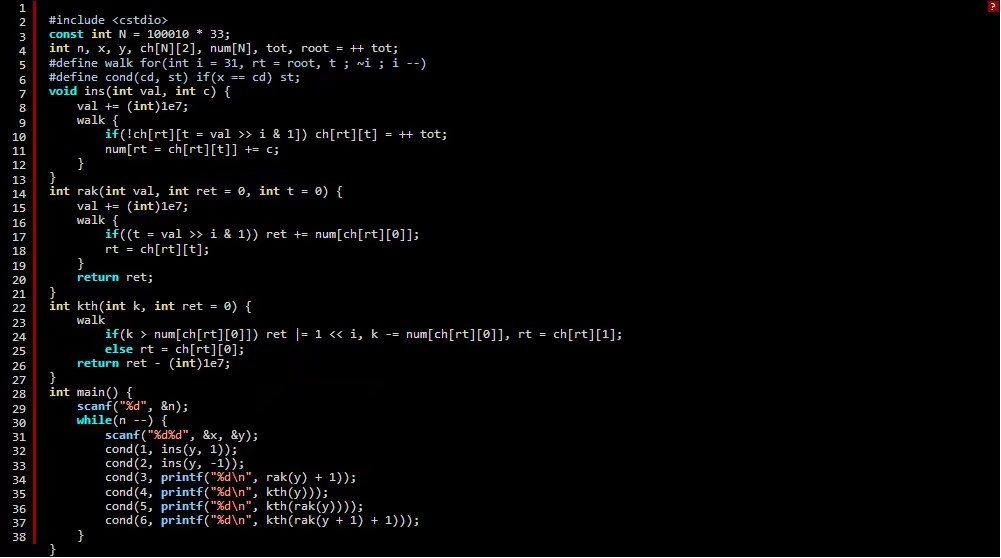
 1 #include <cstdio>
 2 const int N = 100010 * 33;
 3 int n, x, y, ch[N][2], num[N], tot, root = ++ tot;
 4 #define walk for(int i = 31, rt = root, t ; ~i ; i --)
 5 #define cond(cd, st) if(x == cd) st;
 6 void ins(int val, int c) {
 7     val += (int)1e7;
 8     walk {
 9         if(!ch[rt][t = val >> i & 1]) ch[rt][t] = ++ tot;
10         num[rt = ch[rt][t]] += c;
11     }
12 }
13 int rak(int val, int ret = 0, int t = 0) {
14     val += (int)1e7;
15     walk {
16         if((t = val >> i & 1)) ret += num[ch[rt][0]];
17         rt = ch[rt][t];
18     }
19     return ret;
20 }
21 int kth(int k, int ret = 0) {
22     walk
23         if(k > num[ch[rt][0]]) ret |= 1 << i, k -= num[ch[rt][0]], rt = ch[rt][1];
24         else rt = ch[rt][0];
25     return ret - (int)1e7;
26 }
27 int main() {
28     scanf("%d", &n);
29     while(n --) {
30         scanf("%d%d", &x, &y);
31         cond(1, ins(y, 1));
32         cond(2, ins(y, -1));
33         cond(3, printf("%d\n", rak(y) + 1));
34         cond(4, printf("%d\n", kth(y)));
35         cond(5, printf("%d\n", kth(rak(y))));
36         cond(6, printf("%d\n", kth(rak(y + 1) + 1)));
37     }
38 }
View Code

 

你以为这就完了？不。

刚才在写某篇博文（博客里置顶的那个入门到入殓）的时候突然想起来数组模拟指针有一种优美的写法~~~

 1 #include <cstdio>
 2 const int N = 100010 * 33;
 3 int n, x, y, ch[N][2], num[N], tot, root = ++ tot;
 4 #define walk for(int i = 31, rt = root, t ; ~i ; i --)
 5 #define cond(cd, st) if(x == cd) st;
 6 void ins(int val, int c) {
 7     val += (int)1e7;
 8     walk {
 9         if(!rt[ch][t = val >> i & 1]) rt[ch][t] = ++ tot;
10         (rt = rt[ch][t])[num] += c;
11     }
12 }
13 int rak(int val, int ret = 0, int t = 0) {
14     val += (int)1e7;
15     walk {
16         if((t = val >> i & 1)) ret += rt[ch][0][num];
17         rt = rt[ch][t];
18     }
19     return ret;
20 }
21 int kth(int k, int ret = 0) {
22     walk
23         if(k > rt[ch][0][num]) ret |= 1 << i, k -= rt[ch][0][num], rt = rt[ch][1];
24         else rt = rt[ch][0];
25     return ret - (int)1e7;
26 }
27 int main() {
28     scanf("%d", &n);
29     while(n --) {
30         scanf("%d%d", &x, &y);
31         cond(1, ins(y, 1));
32         cond(2, ins(y, -1));
33         cond(3, printf("%d\n", rak(y) + 1));
34         cond(4, printf("%d\n", kth(y)));
35         cond(5, printf("%d\n", kth(rak(y))));
36         cond(6, printf("%d\n", kth(rak(y + 1) + 1)));
37     }
38 }
View Code

 

posted @ 2017-08-10 15:30  KingSann  阅读(1258)  评论(0)  编辑  收藏  举报