深度学习UFLDL老教程笔记1 稀疏自编码器Ⅰ
稀疏自编码器的学习结构:
稀疏自编码器Ⅰ:
神经网络
反向传导算法
梯度检验与高级优化
稀疏自编码器Ⅱ:
自编码算法与稀疏性
可视化自编码器训练结果
Exercise: Sparse Autoencoder
稀疏自编码器Ⅰ这部分先简单讲述神经网络的部分,它和稀疏自编码器关系很大。
神经网络
基本概念:
Topics: connection weights, bias, activation function
神经元(运算单元):连接关系,输入与权值
生物神经元:Synapse, axon, dendrite
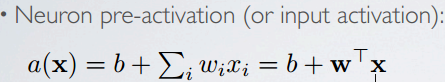
激活函数(映射关系): sigmoid, tanh, linear activation, rectified linear, softmax …
以及激活函数的导数: g(a)=a, g'(a)=1;
g(a) = sigm(a)=1/1+exp(-a), g'(a)=g(a)(1-g(a));
g(a) = tanh(a)=exp(a)-exp(-a)/exp(a)+exp(-a) =exp(2a)-1/exp(2a)+1, g'(a)=1-g(a)^2
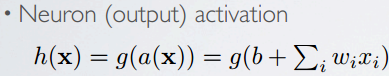
Topics: capacity, decision boundary of neuron
single neuron can solve linearly separable problems,do binary classification
Can't solve non linearly separable problems...
神经网络模型
神经网络就是将许多个单一"神经元"联结在一起。
有输入层,隐藏层(可多层),输出层。
Topics: CAPACITY OF NEURAL NETWORK
Universal approximation theorem (Hornik, 1991):
‣ ''a single hidden layer neural network with a linear output unit can approximate any continuous function arbitrarily well, given enough hidden units''
只要隐含层单元个数足够多,就一个隐藏层的神经网络就能近似表示任何复杂连续函数。这个定理至关重要!
但是这不代表就能找到一个好的算法去找到合适的参数。
这就是神经网络之前研究萧条的原因之一,另一个曾经出现过的原因是一个神经元不能处理非线性可分的分类任务,如实现异或逻辑。
Topics: multilayer neural network
一层不够好,那就多层,甚至现如今火的深度网络。也是有生物理论背景的(visual cortex),也有些方法来训练网络,调整参数的。以后一边学一边总结。
forward propagation 前向传播
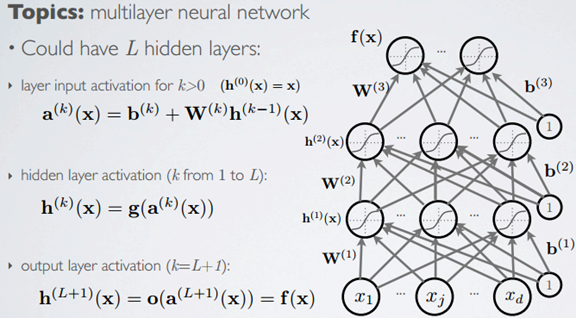
总结为前一层是后一层的输入,但注意中间层的激活函数和输出层的激活函数可能不同。也是forward propagation 前向传播的流程。
Topics: empirical risk minimization, regularization
最后,从机器学习中的监督学习角度来说,假设我们有训练样本集(Xi,Yi ),那么神经网络算法能够提供一种复杂且非线性的假设模型H(X) ,它具有参数W, b,可以以此参数来拟合我们的数据。
即Empirical risk minimization(期望风险/损失最小化)
‣ framework to design learning algorithms
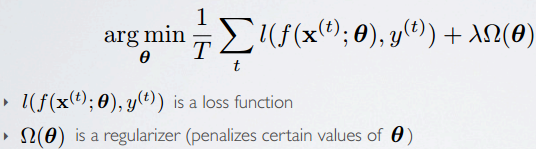
最终学习问题转化为最优化问题。优化方法有许多。
这里介绍常用的一种方法:随机梯度下降法,stochastic gradient descent (SGD),注意下图用的是stochastic随机(单个each),而ufldl老教程用的是batch批量梯度下降法来训练神经网络,当然还可以有min-batch(部分)。且ufldl实验中使用了L-BFGS optimization algorithm的函数包来进行优化。L-BFGS is a limited-memory quasi-Newton code for unconstrained optimization.

上图的算法逻辑清晰,但是细节实现还有很多,比如:LOSS FUNCTION,GRADIENT COMPUTATION,等,如下图

其中细节太多,下面先只学习反向传播算法(backpropagation algorithm),它是求梯度(偏导数)过程中的一种重要方法。
反向传播算法
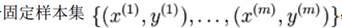
对于单个样例代价函数为:
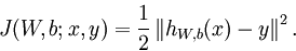
m个样例的数据集整体代价函数为:
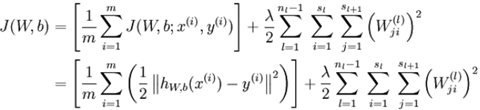
注:权重衰减是作用于 W而不是b 。
梯度下降法
梯度下降法中每一次迭代都按照如下公式对参数W 和 b进行更新:

以上其实是批量梯度下降法的迭代框架。其中
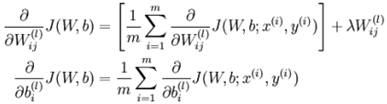
反向传播
而反向传播算法是用来计算上述的偏导函数:
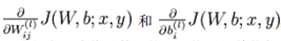
因为,
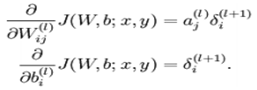
而BP求残差(误差)
注意:做反向传播算法之前要先做前向传播算法。以下是BP思想及其求残差的实现方式。

反向传播算法可表示为以下几个步骤:

梯度下降算法全面总结
实现批量梯度下降法中的一次迭代:

现在,我们可以重复梯度下降法的迭代步骤来减小代价函数J(W,b) 的值,进而求解我们的神经网络。
题外话:就上图所述,其实只是个框架,具体很多细节还是有很多需要注意的。比如,参数的初始化问题,规则项中也有很大的文章可以做(这里用的是L2,那L1呢,功能和含义是不一样的,等等)。以外还有模型选择,交叉验证等工作,限于这章主题和篇幅,以后另加学习和总结。
梯度检验与高级优化
就简单总结下好了,不要整多,要化繁为简。

声明:
不要将本博客用作为商业目的,并且本人博客使用的内容仅仅作为个人学习,其中包括引用的或没找到出处而未引用的内容。
转载请注明,本文地址:http://www.cnblogs.com/JayZen/p/4119061.html
参考:
UFLDL教程
Hugo Larochelle nn course



 浙公网安备 33010602011771号
浙公网安备 33010602011771号