20162325 金立清 S2 W9 C18

20162325 2017-2018-2 《程序设计与数据结构》第9周学习总结

教材学习内容概要

堆是一棵完全二叉树，其中每个元素大于等于其所有子结点的值。
向堆中添加一个元素的方法是，首先将这个元素添加为叶结点，然后将其向上移动到合适的位置。
从堆中删除最大元素的方法是，首先将这个元素的叶结点来取代根，然后将其向下移动到合适的位置。
堆排序利用堆的基本特性对一组元素进行排序。
优先队列不是FIFO队列。它根据优先级排列元素，而不是根据它们进入队列的次序来排序。

堆

堆的定义如下：
（1）堆是一颗完全二叉树；
（2）堆树中某个节点的值总是不大于或不小于其孩子节点的值；
（3）堆树中每个节点的子树都是堆树。
当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。如下图所示，左边为最大堆，右边为最小堆。

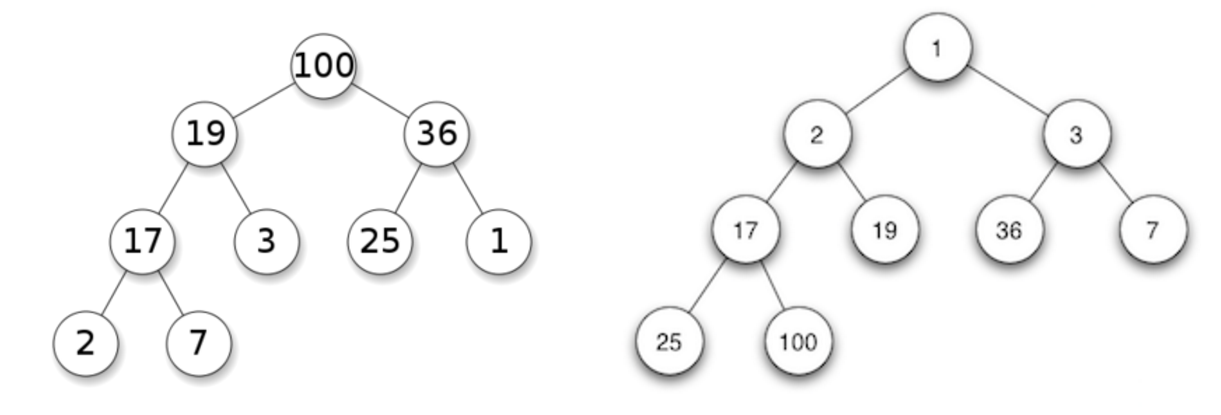
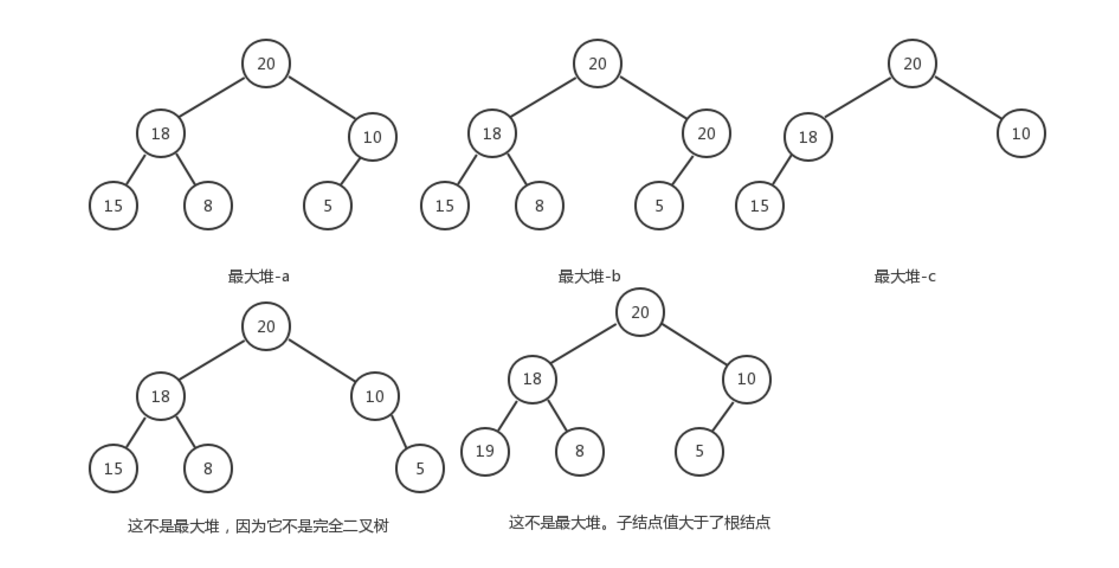
辨析（以最大堆为例）：

这里需要注意的是：在多个子树中，并不是说其中一个子树的父结点一定大于另一个子树的儿子结点。最大堆是树结构，而且一定要是完全二叉树。

备注：本章集中讨论最大堆，所有的操作通过翻转比较运算后都可适用于最小堆。如有需要可参考最小堆构建、插入、删除的过程图解-CSDN博客理解。

向堆中添加一个元素

最大堆的插入操作可以简单看成是结点上浮。当我们在向堆中插入一个结点我们必须满足完全二叉树的标准，那么被插入结点的位置的是固定的。而且要满足父结点关键字值不小于子结点关键字值，那么我们就需要去移动父结点和子结点的相互位置关系。具体的位置变化，如下图：

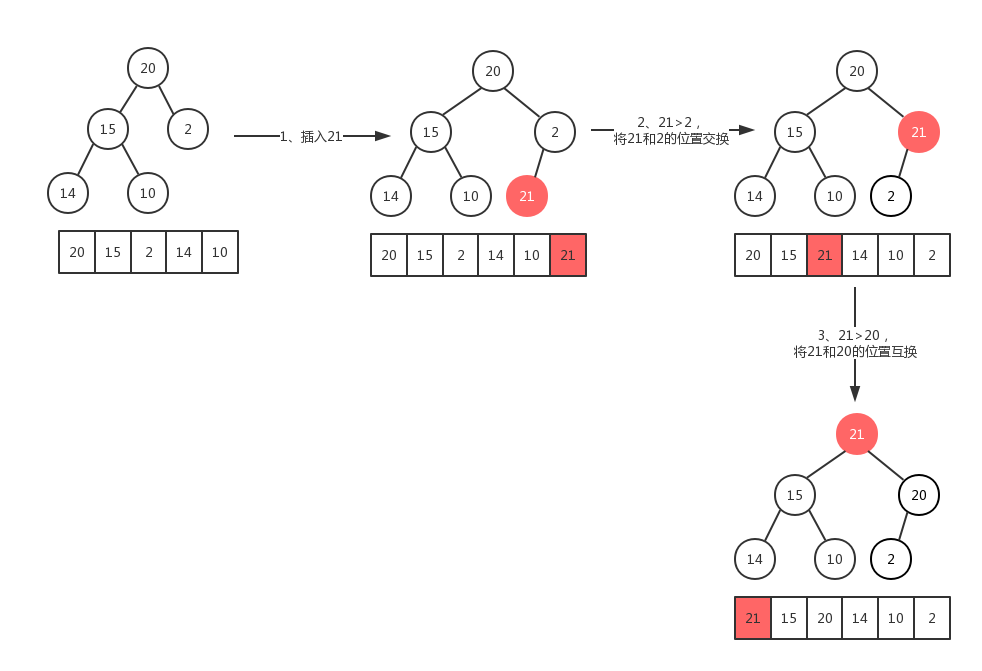
由于堆是一棵完全二叉树，存在n个元素，那么他的高度为:log2(n+1)，这就说明代码中的for循环会执行O(log2(n))次。因此插入函数的时间复杂度为：O(log2(n))。

从堆中删除最大元素

最大堆的删除操作，总是从堆的根结点删除元素。同样根元素被删除之后为了能够保证该树还是一个完全二叉树，我们需要来移动完全二叉树的最后一个结点，让其继续符合完全二叉树的定义，从这里可以看作是最大堆最后一个结点的下沉（也就是下文提到的结点1）操作。例如在下面的最大堆中执行删除操作：

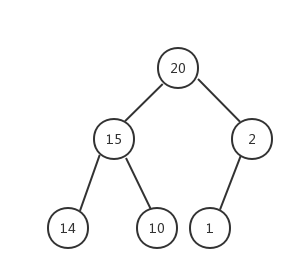
现在对上面👆最大堆做删除，对于最大堆的删除，我们不能自己进行选择删除某一个结点，我们只能删除堆的根结点。(⚠️⚠️⚠️)

第一步，我们删除上图中的根结点20；
当删除根结点20之后明显不是一个完全二叉树，更确切地说被分成了两棵树。
我们需要移动子树的某一个结点来充当该树的根节点，那么在(15,2,14,10,1)这些结点中移动哪一个呢？显然是移动结点1，如果移动了其他结点（比如14，10）就不再是一个完全二叉树了。

对上面三步图示如下：

显然现在看来该二叉树虽然是一个完全二叉树，但是它并不符合最大堆的相关定义，我们的目的是要在删除完成之后，该完全二叉树依然是最大堆。因此就需要我们来做一些相关的操作！


1）、此时在结点（15，2）中选择较大的一个和1做比较，即15 > 1的，所以15上浮到之前的20的结点处。
2）、同第1步类似，找出（14，10）之间较大的和1做比较，即14>1的，所以14上浮到原来15所处的结点。
3）、因为原来14的结点是叶子结点，所以将1放在原来14所处的结点处。

同最大堆的插入操作类似，同样包含n个元素的最大堆，其高度为:log2(n+1)，其时间复杂度为：O(log2(n))。

总结：由此可以看出，在已经确定的最大堆中做删除操作，被删除的元素是固定的，需要被移动的结点也是固定的，这里我说的被移动的元素是指最初的移动，即最大堆的最后一个元素。移动方式为从最大的结点开始比较。

堆的实现

具体参考书上P404--408的代码，另外在查阅资料的时候，看到最大堆（创建、删除、插入和堆排序） - 简书中与书上的例子不同，作者称：比起用链表的方式来实现（需要添加一个额外的指针来指向该结点的父结点。此时就包括了左子结点指针、右子结点指针和父结点指针，那么空链的数目有可能是很大的，比如叶子结点的左右子结点指针和根结点的父结点指针）更建议用使用数组实现，在二叉树进行遍历的方法分为：先序遍历、中序遍历、后序遍历和层序遍历。我们可以通过层序遍历的方式将二叉树结点存储在数组中，因为最大堆是完全二叉树不会存在数组的空间浪费。

堆排序

堆排序和合并排序一样，是一种时间复杂度为O(nlgn)的算法，同时和插入排序一样，是一种就地排序算法(不需要额外的存储空间)。堆可以被视为一种完全二叉树，即树里面除了最后一层其他层都是填满的。也正是因为这样，树里面每个节点的子女和双亲节点的序号都可以根据当前节点的序号直接求出。

如上图所示，1位置的子女节点分别为2,3 2节点的子女节点为4,5 2的双亲节点为1 考察其他节点也很容易发现上述关系。最大堆是一种特殊的堆，其特点是每个双亲节点的值都比子女节点大。他的这一特点使得他可以实现nlgn的就地排序。现在我们先来看看怎么构建和保持一个最大堆。

最大堆的构建和保持

我们现在有一个数组A,大小是n，假设其中元素按照完全二叉树的方式排列。如何将其构造成一个最大堆？首先我们知道最大堆的每个子树都符合最大堆的性质（根节点值大于所有子节点）。同时我们知道序号为（n/2+1）_{n的元素都是叶子节点（因为其子女节点的序号都大于n，即说明没有子女节点），因此我们构建最大堆的操作就在序号为1}n/2的元素内进行（其他元素已满足最大堆性质）。我们定义如下操作maxify(i):将以i位置节点为根的子树改造成最大堆。其操作内容如下：对于每个节点i，我们考察他与子女节点的大小，如果他比某个子女节点小，则将他与子女节点中最大的那个互换位置，然后在相应的子女节点位置重复操作，直到到达堆的叶子节点或者考察的位置比子女节点的值都要大为止。由此可知我们构造最大堆buildmaxheap的过程就是在每个内部节点上调用maxify过程，依次到树的根部，此时其左右子树都是最大堆，现在在根节点调用maxify即完成了最大堆的构造。

堆排序的操作

     有了最大堆的基础结构后，我们就可以利用最大堆的性质进行排序HeapSort，我们从根节点开始操作，因为根节点是这个数组中最大的元素，因此我们将其于数组中最后一个元素对换（排序后，最大元素应该在最后）将heapsize减1，然后再在根节点出调用maxify过程将新的堆重新最大堆化。依次循环，我们每次都能将现有堆中最大的元素放到堆末尾。最后就完成了整个排序过程。操作情况见下图（只列出了前4步），从堆中得到的元素序列是降序有序序列 。

优先队列

优先队列是一种用来维护一组元素构成的结合S的数据结构，其中每个元素都有一个关键字key，元素之间的比较都是通过key来比较的。优先队列包括最大优先队列和最小优先队列，优先队列的应用比较广泛，比如作业系统中的调度程序，当一个作业完成后，需要在所有等待调度的作业中选择一个优先级最高的作业来执行，并且也可以添加一个新的作业到作业的优先队列中。
我们知道队列是遵循先进先出（First-In-First-Out）模式的，但有些时候需要在队列中基于优先级处理对象。比方说我们有一个每日交易时段生成股票报告的应用程序，需要处理大量数据并且花费很多处理时间。客户向这个应用程序发送请求时，实际上就进入了队列。我们需要首先处理优先客户再处理普通用户。在这种情况下，Java的PriorityQueue(优先队列)会很有帮助。
PriorityQueue是基于优先堆的一个无界队列，这个优先队列中的元素可以默认自然排序或者通过提供的Comparator（比较器）在队列实例化的时排序。
优先队列不允许空值，而且不支持non-comparable（不可比较）的对象，比如用户自定义的类。优先队列要求使用Java Comparable和Comparator接口给对象排序，并且在排序时会按照优先级处理其中的元素。
优先队列的头是基于自然排序或者Comparator排序的最小元素。如果有多个对象拥有同样的排序，那么就可能随机地取其中任意一个。当我们获取队列时，返回队列的头对象。
优先队列的大小是不受限制的，但在创建时可以指定初始大小。当我们向优先队列增加元素的时候，队列大小会自动增加。
PriorityQueue是非线程安全的，所以Java提供了PriorityBlockingQueue（实现BlockingQueue接口）用于Java多线程环境。
优先队列的实现中，我们可以选择堆数据结构，最大优先队列可以选用大堆，最小优先队列可以选用小堆来实现。下面以最大优先队列来讲解其原理。最大优先队列一般包括将一个元素插入到集合S中、返回集合S中具有最大key的元素、返回并删除集合S中具有最大key的元素等。

教材学习中的问题和解决过程

问题1：书上LinkedMaxHeap写道heapifyAdd，heapifyRemove，没太明白heapify含义
问题1解决方案：
API文档里没找到，百度了下，“数组建堆（heapify）”，
堆排序——BuildHeap和Heapify函数的实现里说：堆排序的时间，主要由建立初始堆和反复重建堆这两部分的时间开销构成，它们均是通过调用Heapify实现的。
Heap和Heapify - YRB - 博客园里称：heapify()是指最大heapify。我们只需要从 k = N / 2开始，在k >= 1的条件下对 k 进行sink()，然后k--就可以了。
可能就是堆方法的前缀表达吧。
问题2：不太理解P407 HeapNode中有关getParentAdd方法的代码

public HeapNode<T> getParentAdd (HeapNode<T> last)
    {
        HeapNode<T> result = last;

        while ((result.parent != null) && (result.parent.left != result))
            result = result.parent;

        if (result.parent != null)
            if (result.parent.right == null)
                result = result.parent;
            else
            {
                result = (HeapNode<T>) result.parent.right;
                while (result.left != null)
                    result = (HeapNode<T>) result.left;
            }
        else
            while (result.left != null)
                result = (HeapNode<T>) result.left;

        return result;
    }

问题2解决方案：

请教搭档，一直不予理睬；后来请教马军，但他也没能看懂…打算课间请教老师。

代码调试中的问题和解决过程

问题1：参考娄老师给的PriorityQueue代码时,显示找不到addElement方法和removeMin方法
解决方案：参考搭档博客，分别改成add、removeMax，将PriorityQueueNode改成PriorityQueueNode。
问题2：HeapNode用到了十六章里的BTNode，因为在两个package里，import无效
解决方案：根据张泰毓的建议，直接把BTNode从16章里拖到18章。

代码托管

上周考试错题总结

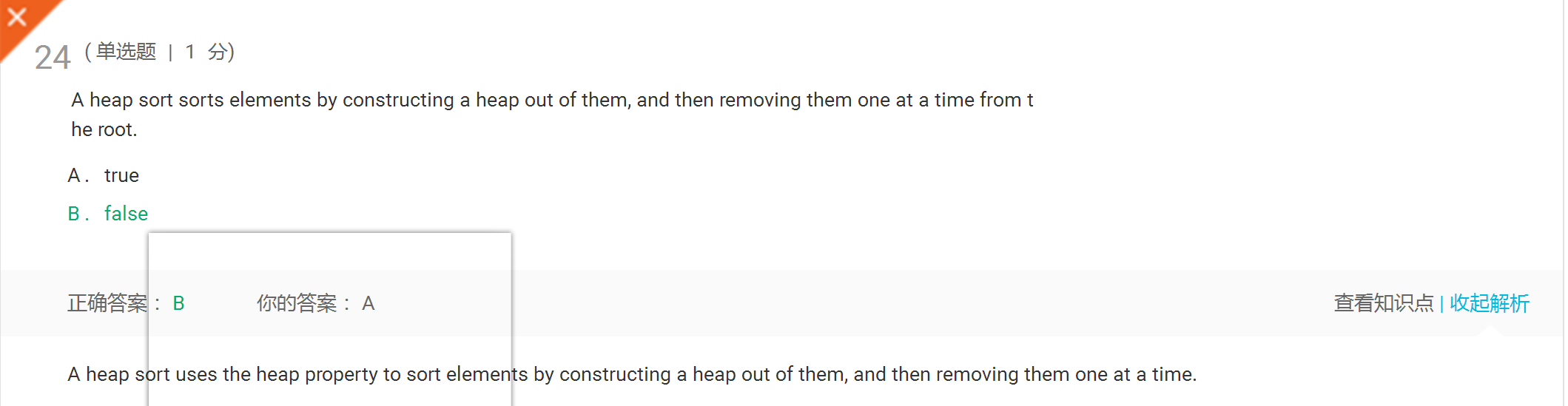
解答：解析和正确答案相符，所选答案是课本内容，不知为何判错？

解答：
解答：是删除堆，不是从根目录

本周结对学习情况

结对搭档
- 20162311
结对学习内容
- 理解代码（哈夫曼树的构造）

其他（感悟、思考等，可选）

这周在二叉树的基础上学习了堆，哈夫曼树（但对编码解码还没太琢磨透，课下再花时间尽量能自己编出来）

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）
目标	5000行	30篇	400小时
第一周	58/	1/1	10/10
第二周			8/18
第三周	134/	3/4	12/ 30
第四周		2/6	12/42
第五&六周	750/ 6595	5/11	24/66
第七周	764/7068	7/13	18/84
第八周	888/7956	9/15	20/104
第九周	475/8431	12/18	22/126

计划学习时间: 22小时
实际学习时间: 22小时
改进情况：受别科小组任务和本周团队作业的影响，这周花在Java学习上的时间还不够，下周注意；另外效率有待提高！

参考资料

posted @ 2017-11-05 20:08 20162325金立清阅读(359) 评论(1) 编辑收藏举报

刷新页面返回顶部