20162325 金立清 S2 W8 C17
20162325 2017-2018-2 《程序设计与数据结构》第8周学习总结
教材学习内容概要
二叉查找树是一棵二叉树,对于其中的每个结点,左子树上的元素小于父结点的值,而右子树上的元素大于等于父结点的值。
最有效的二叉树是平衡的,所以每次比较时可以排除一半的元素。
如果没有其他操作,二叉查找树的树形由元素的添加次序来决定。
当从二叉查找树中删除元素时要考虑三种情形,其中的两种比较简单。
当从二叉查找树中删除两个子结点的结点时,比较好的办法是用它的中序后继来取代它。
可以对二叉查找树进行旋转以恢复平衡。
二叉查找树定义:
- 又称为是二叉排序树(Binary Sort Tree)或二叉搜索树。二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
1) 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2) 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
3) 左、右子树也分别为二叉排序树;
4) 没有键值相等的节点。
- 二叉查找树的性质:对二叉查找树进行中序遍历,即可得到有序的数列。
- 二叉查找树的时间复杂度:它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡。我们追求的是在最坏的情况下仍然有较好的时间复杂度,这就是平衡查找树设计的初衷。
- 二叉查找树的高度决定了二叉查找树的查找效率。
二叉查找树的插入过程
- 若当前的二叉查找树为空,则插入的元素为根节点。
- 若插入的元素值小于根节点值,则将元素插入到左子树中。
- 若插入的元素值不小于根节点值,则将元素插入到右子树中。
二叉查找树的删除
- 分三种情况进行处理:
1. p为叶子节点,直接删除该节点,再修改其父节点的指针(注意分是根节点和不是根节点),如图a。
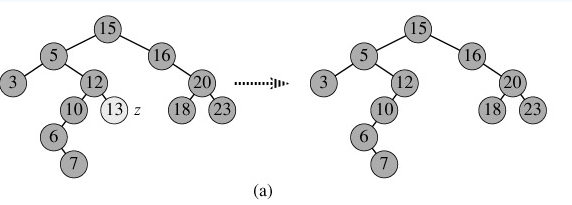
2. p为单支节点(即只有左子树或右子树)。让p的子树与p的父亲节点相连,删除p即可;(注意分是根节点和不是根节点);如图b。
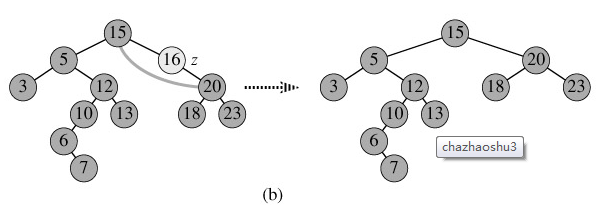
3. p的左子树和右子树均不空。找到p的后继y,因为y一定没有左子树,所以可以删除y,并让y的父亲节点成为y的右子树的父亲节点,并用y的值代替p的值;或者方法二是找到p的前驱x,x一定没有右子树,所以可以删除x,并让x的父亲节点成为y的左子树的父亲节点。如图c。
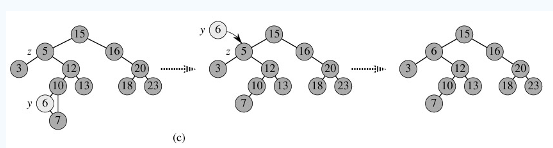
平衡二叉树
-
二叉排序树集中了数组的查找优势以及链表的插入、删除优势,因此在数据结构中占有一定的地位。但在一定的情况下二叉排序树又有可能变为链表,例如插入从1~100的数,这时进行数据查找的效率就要降低。
-
为了解决二叉排序树这种左右子树深度不均匀的情况引入了一种平衡二叉树(AVLTree):任何一个节点的左右子树深度差不超过1.通过这个限定,阻止了二叉树的左右子树深度差较大的情况,维持了二叉树的稳定。
-
为了让二叉树的左右子树深度差不超过1,需要对节点进行旋转,具体参考{数据结构—平衡二叉树](http://www.cnblogs.com/PerkinsZhu/p/5824015.html)
教材学习中的问题和解决过程
-
问题1:对Comparable接口的认知,与Comparator、compareTo、compare进行比较
-
问题1解决方案:
二叉查找树要求所有的项都能够排序。要写出一个一般的类,我们需要提供一个接口来表示这个性质。这个接口就是Comparable,该接口告诉我们,树中的两项总可以使用CompareTo()方法比较。
public interface Comparable<t></t>
此接口强行对实现它的每个类的对象进行整体排序。这种排序被称为类的自然排序,类的 compareTo 方法被称为它的自然比较方法。
备注:已经被大多数的常用类型实现

compareTo
int compareTo(T o)
比较此对象与指定对象的顺序。如果该对象小于、等于或大于指定对象,则分别返回负整数、零或正整数。
public interface Comparator<t></t>
强行对某个对象 collection 进行整体排序 的比较函数。可以将 Comparator 传递给 sort 方法(如 Collections.sort 或 Arrays.sort),从而允许在排序顺序上实现精确控制。还可以使用 Comparator 来控制某些数据结构(如有序 set或有序映射)的顺序,或者为那些没有自然顺序的对象 collection 提供排序。
备注:仅有少数类实现了这个接口

int compare(T o1,T o2)
比较用来排序的两个参数。根据第一个参数小于、等于或大于第二个参数分别返回负整数、零或正整数。
代码调试中的问题和解决过程
- 已写进实验博客中
代码托管
上周考试错题总结
-
错题一:

-
分析:
这里的all nodes 其实是指同一层上的all nodes,我发现有些时候不能直译,抠字眼,得顺着特征性质来思考 -
错题二:
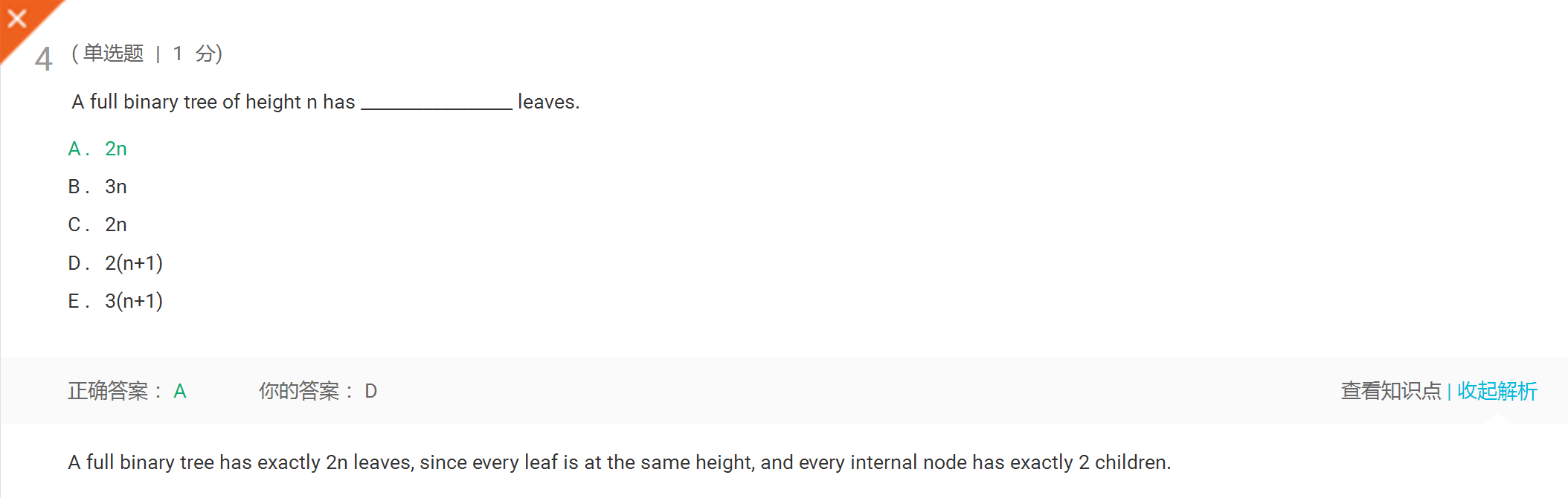
-
分析:
记忆里自己没做错啊…….可能是不小心选到相邻项上了,下次注意
本周结对学习情况
- 20162311
- 结对学习内容
- 实验二
其他(感悟、思考等,可选)
- 这周主要精力都花在实验二上,参考了很多博客,也求助了不少同学,勉强按时完成,但自身掌握地还是不到位,打算边学边补。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 58/ | 1/1 | 10/10 | |
| 第二周 | 8/18 | |||
| 第三周 | 134/ | 3/4 | 12/ 30 | |
| 第四周 | 2/6 | 12/42 | ||
| 第五&六周 | 750/ 6595 | 5/11 | 24/66 | |
| 第七周 | 764/7068 | 7/13 | 18/84 | |
| 第八周 | 888/7956 | 9/15 | 20/104 |
-
计划学习时间: 18小时
-
实际学习时间: 20小时
-
改进情况:阅读了很多资料


