树-实验报告
树-实验报告
代码托管地址
实验-1实现二叉树
实验要求
参考教材p375,完成链树LinkedBinaryTree的实现(getRight,contains,toString,preorder,postorder)
用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试
实验步骤
get Right
- 参考get Left方法把left改成right即可
public LinkedBinaryTree<T> getRight() {
if (root == null)
throw new EmptyCollectionException ("Get left operation "
+ "failed. The tree is empty.");
LinkedBinaryTree<T> result = new LinkedBinaryTree<T>();
result.root = root.getRight();
return result;
}
contains
- 从意思上觉得和find方法相近,调用find方法,返回boolean类型
public boolean contains (int target) {
BTNode<T> node = null;
if (root != null)
node = root.find(target);
if (node == null)
return false;
else
return true;
}
preorder、postorder
- 这里用到了迭代器和递归的思路,参考书中实现中序遍历的代码,改变一下左子树、根、右子树的顺序即可
public void inorder (ArrayIterator<T> iter)
{
//左根右
if (left != null)
left.inorder (iter);
iter.add (element);
if (right != null)
right.inorder (iter);
}
public void preorder (ArrayIterator<T> iter) {
//根左右
iter.add (element);
if (left != null)
left.preorder (iter);
if (right != null)
right.preorder (iter);
}
public void postorder (ArrayIterator<T> iter) {
//左右根
if (left != null)
left.postorder (iter);
if (right != null)
right.postorder (iter);
iter.add (element);
}
实验-2中序先序序列构造二叉树
实验要求
基于LinkedBinaryTree,实现基于(中序,先序)序列构造唯一一棵二㕚树的功能,比如教材P372,给出HDIBEMJNAFCKGL和ABDHIEJMNCFGKL,构造出附图中的树
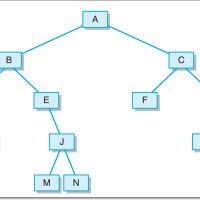
实验思路
参考实现二叉树(链式存储结构)http://www.jb51.net/article/88460.htm)
测试结果
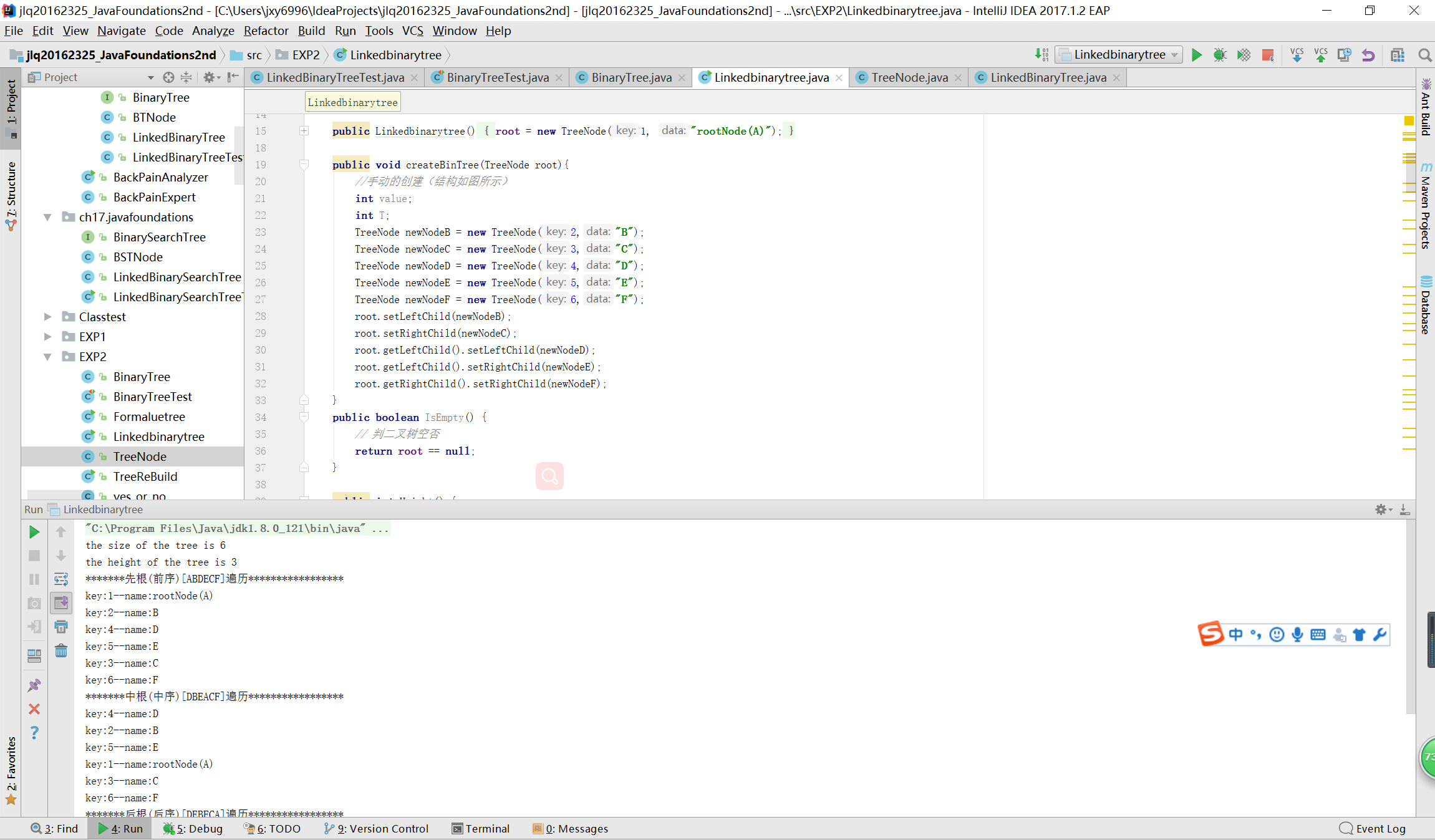
实验-3决策树
实验要求
完成PP16.6,利用决策树来完成20问yes or no的游戏
实验知识点
- 一棵决策树包含一个根结点、若干个内部结点和若干个叶结点。叶结点对应于决策结果,其他每个结点则对应于一个属性测试。
- 在理顺左右子树和根节点对应关系的前提下,修改BackPainExpert中的问题并写一个简单的驱动测试
测试结果
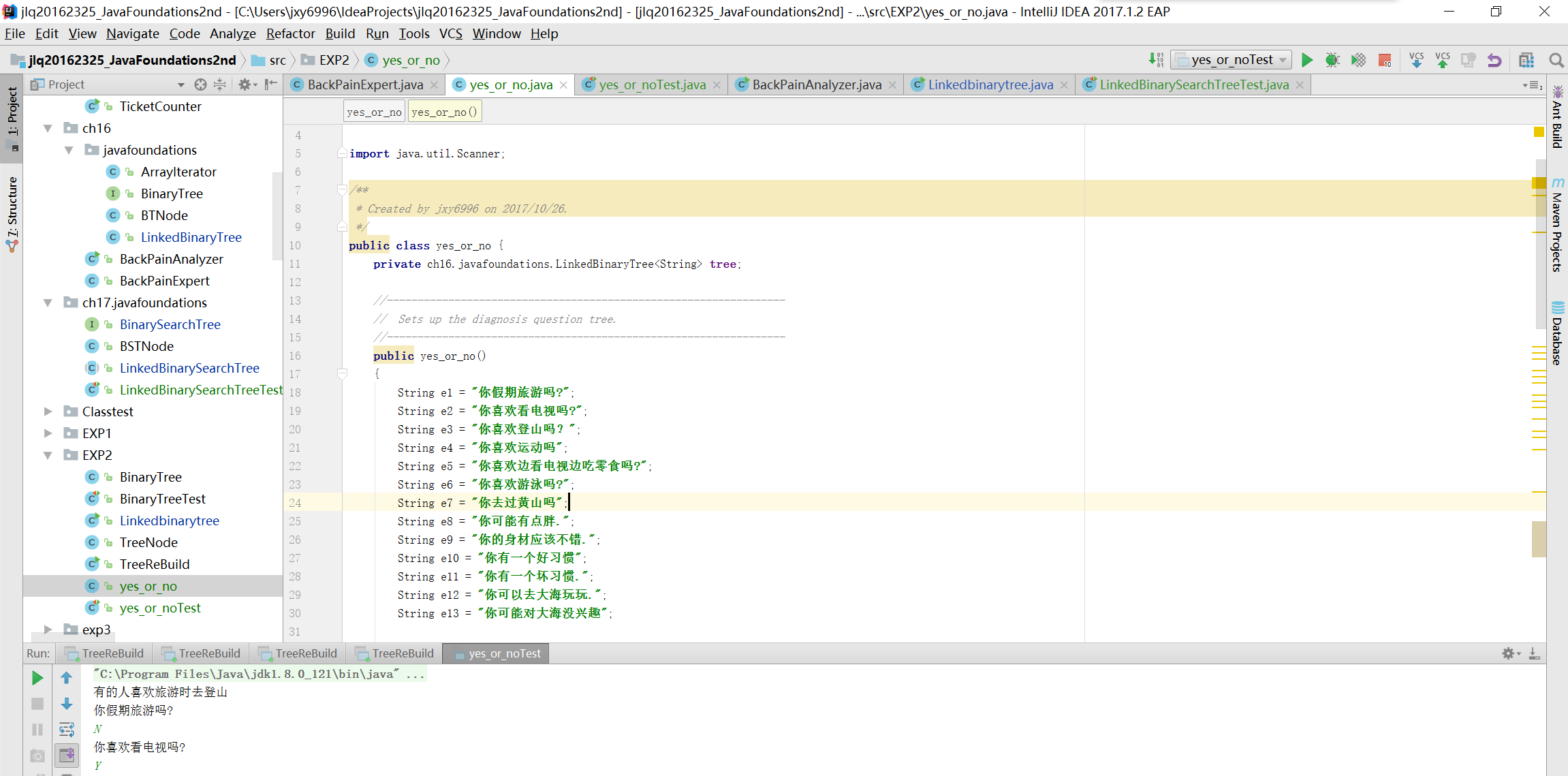
实验-4表达式树
实验要求
完成PP16.8,使用二叉树表示表达式树
实验思路
实验代码
原本的Node与已有的BTNode功能相近,就改用了现成的。
package EXP2;
import ch16.javafoundations.BTNode;
import java.util.ArrayList;
/**
* Created by jxy6996 on 2017/10/26.
*/
public class Formaluetree {
private String s="";
private BTNode root; //根节点
/**
* 创建表达式二叉树
* @param str 表达式
*/
public void creatTree(String str){
//声明一个数组列表,存放的操作符,加减乘除
ArrayList<String> operList = new ArrayList<String>();
//声明一个数组列表,存放节点的数据
ArrayList<BTNode> numList = new ArrayList<BTNode>();
//第一,辨析出操作符与数据,存放在相应的列表中
for(int i=0;i<str.length();i++){
char ch = str.charAt(i); //取出字符串的各个字符
if(ch>='0'&&ch<='9'){
s+=ch;
}else{
numList.add(new BTNode(s));
s="";
operList.add(ch+"");
}
}
//把最后的数字加入到数字节点中
numList.add(new BTNode(s));
while(operList.size()>0){ //第三步,重复第二步,直到操作符取完为止
//第二,取出前两个数字和一个操作符,组成一个新的数字节点
BTNode<String> left = numList.remove(0);
BTNode<String> right = numList.remove(0);
String oper = operList.remove(0);
BTNode<String> node = new BTNode(oper);
node.setLeft(left);
node.setRight(right);
numList.add(0,node); //将新生的节点作为第一个节点,同时以前index=0的节点变为index=1
}
//第四步,让根节点等于最后一个节点
root = numList.get(0);
}
/**
* 输出结点数据
*/
public void output(){
output(root); //从根节点开始遍历
}
/**
* 输出结点数据
* @param node
*/
public void output(BTNode node){
if(node.getLeft()!=null){ //如果是叶子节点就会终止
output(node.getLeft());
}
System.out.print(node.getElement()); //遍历包括先序遍历(根左右)、中序遍历(左根右)、后序遍历(左右根)
if(node.getRight()!=null){
output(node.getRight());
}
}
public static void main(String[] args) {
Formaluetree tree = new Formaluetree();
tree.creatTree("45+23*56/2-5");//创建表达式的二叉树
tree.output();//输出验证
}
}
实验问题与解决措施
-
原代码中有一行用到了BTNode里没有的方法

-
解决措施如下:
BTNode<String> node = new BTNode(oper);
node.setLeft(left);
node.setRight(right);
测试结果
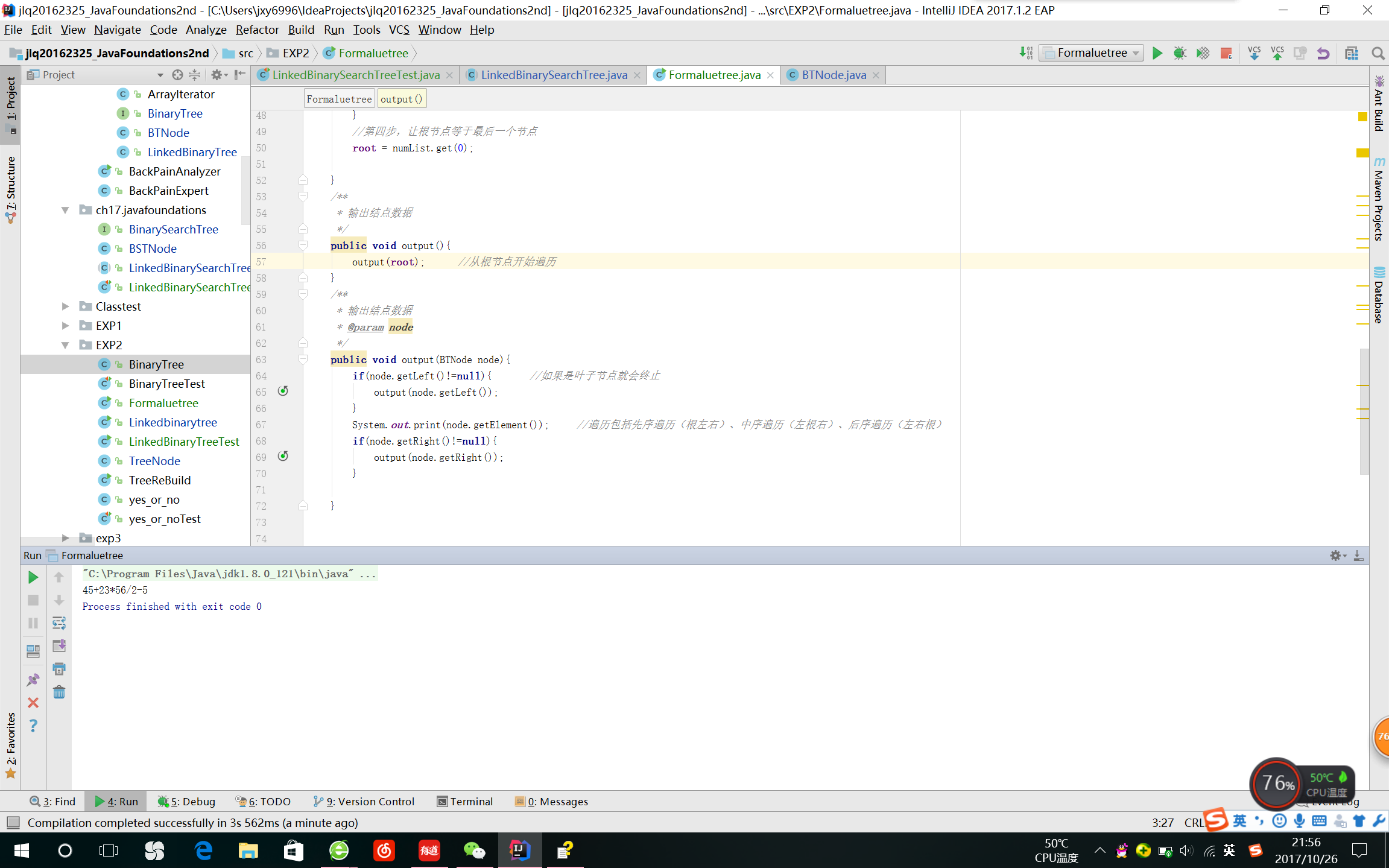
实验-5二叉查找树
实验要求
完成PP17.1,完成LinkedBinarySearchTree类的实现,特别是findMax和findMin两个操作
实验思路
- 对一棵二叉排序树采用中序遍历进行输出的数据一定是递增序列,所以调用inorder()方法
public T findMin() {
ArrayIterator<T> iter = (ArrayIterator<T>)inorder();
return iter.get(0);
}
public T findMax() {
ArrayIterator<T> iter = (ArrayIterator<T>)inorder();
return iter.get(iter.size()-1);
}
测试结果
实验-6红黑树分析
实验要求
参考http://www.cnblogs.com/rocedu/p/7483915.html对Java中的红黑树(TreeMap,HashMap)进行源码分析
实验知识点
- 参考(通过分析JDK 源代码研究 TreeMap 红黑树算法实现)[http://www.cnblogs.com/abc8023/p/4339021.html#D]
红黑树
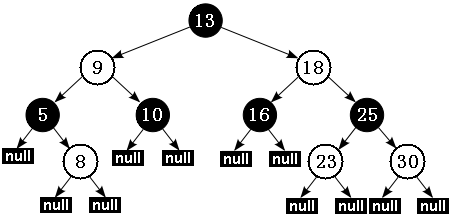
-
备注:白色代表红色。
-
排序二叉树虽然可以快速检索,但在最坏的情况下:如果插入的节点集本身就是有序的,要么是由小到大排列,要么是由大到小排列,那么最后得到的排序二叉树将变成链表:所有节点只有左节点(如果插入节点集本身是大到小排列);或所有节点只有右节点(如果插入节点集本身是小到大排列)。在这种情况下,排序二叉树就变成了普通链表,其检索效率就会很差。
-
为了改变排序二叉树存在的不足,Rudolf Bayer 与 1972 年发明了另一种改进后的排序二叉树:红黑树,他将这种排序二叉树称为“对称二叉 B 树”,而红黑树这个名字则由 Leo J. Guibas 和 Robert Sedgewick 于 1978 年首次提出。
-
红黑树是一个更高效的检索二叉树,因此常常用来实现关联数组。典型地,JDK 提供的集合类 TreeMap 本身就是一个红黑树的实现。
-
红黑树在原有的排序二叉树增加了如下几个要求:
Java 实现的红黑树
- 性质 1:每个节点要么是红色,要么是黑色。
- 性质 2:根节点永远是黑色的。
- 性质 3:所有的叶节点都是空节点(即 null),并且是黑色的。
- 性质 4:每个红色节点的两个子节点都是黑色。(从每个叶子到根的路径上不会有两个连续的红色节点)
- 性质 5:从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点。
性质 3 中指定红黑树的每个叶子节点都是空节点,而且并叶子节点都是黑色。但 Java 实现的红黑树将使用 null 来代表空节点,因此遍历红黑树时将看不到
黑色的叶子节,看到每个叶子节点都是红色的。
性质 4 则保证了从根节点到叶子节点的最长路径的长度不会超过任何其他路径的两倍。假如有一棵黑色高度为 3 的红黑树:从根节点到叶节点的最短路径长度是 2,该路径上全是黑色节点(黑节点 - 黑节点 - 黑节点)。最长路径也只可能为 4,在每个黑色节点之间插入一个红色节点(黑节点 - 红节点 - 黑节点 - 红节点 - 黑节点),性质 4 保证绝不可能插入更多的红色节点。由此可见,红黑树中最长路径就是一条红黑交替的路径。
性质 5中表示红黑树从根节点到每个叶子节点的路径都包含相同数量的黑色节点,因此从根节点到叶子节点的路径中包含的黑色节点数被称为树的“黑色高度(black-height)”。
1.什么是Map?
-
在数组中我们是通过数组下标来对其内容索引的,而在Map中我们通过对象来对对象进行索引,用来索引的对象叫做key,其对应的对象叫做value。这就是我们平时说的键值对。
-
HashMap通过hashcode对其内容进行快速查找,而 TreeMap中所有的元素都保持着某种固定的顺序,如果你需要得到一个有序的结果你就应该使用TreeMap(HashMap中元素的排列顺序是不固定的)。
2.两种常规Map实现
- HashMap:基于哈希表实现。使用HashMap要求添加的键类明确定义了hashCode()和equals()[可以重写hashCode()和equals()],为了优化HashMap空间的使用,您可以调优初始容量和负载因子。
(1)HashMap(): 构建一个空的哈希映像
(2)HashMap(Map m): 构建一个哈希映像,并且添加映像m的所有映射
(3)HashMap(int initialCapacity): 构建一个拥有特定容量的空的哈希映像
(4)HashMap(int initialCapacity, float loadFactor): 构建一个拥有特定容量和加载因子的空的哈希映像
- TreeMap:基于红黑树实现。TreeMap没有调优选项,因为该树总处于平衡状态。
(1)TreeMap():构建一个空的映像树
(2)TreeMap(Map m): 构建一个映像树,并且添加映像m中所有元素
(3)TreeMap(Comparator c): 构建一个映像树,并且使用特定的比较器对关键字进行排序
(4)TreeMap(SortedMap s): 构建一个映像树,添加映像树s中所有映射,并且使用与有序映像s相同的比较器排序
3.两种常规Map性能
HashMap:适用于在Map中插入、删除和定位元素。
Treemap:适用于按自然顺序或自定义顺序遍历键(key)。
4.比较
HashMap通常比TreeMap快一点(树和哈希表的数据结构使然),建议多使用HashMap,在需要排序的Map时候才用TreeMap。
TreeMap
- [1] TreeMap的底层使用了红黑树来实现,像TreeMap对象中放入一个key-value 键值对时,就会生成一个Entry对象,这个对象就是红黑树的一个节点,其实这个和HashMap是一样的,一个Entry对象作为一个节点,只是这些节点存放的方式不同。
- [2] 存放每一个Entry对象时都会按照key键的大小按照二叉树的规范进行存放,所以TreeMap中的数据是按照key从小到大排序的。
TreeMap类源码:
public class TreeMap<K,V>
extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable, java.io.Serializable
{
/**
* The comparator used to maintain order in this tree map, or
* null if it uses the natural ordering of its keys.
*
* @serial
*/
private final Comparator<? super K> comparator;
// 根节点
private transient Entry<K,V> root = null;
/**
* The number of entries in the tree
* 树中的节点数,即entry对象的个数
*/
private transient int size = 0;
/**
* The number of structural modifications to the tree.
* 树修改的次数
*/
private transient int modCount = 0;
TreeMap的内部类Entry<K k,V v>即一个节点:
static final class Entry<K,V> implements Map.Entry<K,V> {
// 关键字key 按照key的哈希值来存放
K key;
// key对应的value值
V value;
// 左节点
Entry<K,V> left = null;
// 右节点
Entry<K,V> right = null;
// 父节点
Entry<K,V> parent;
boolean color = BLACK;
/**
* Make a new cell with given key, value, and parent, and with
* {@code null} child links, and BLACK color.
*/
Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
/**
* Returns the key.
*
* @return the key
*/
public K getKey() {
return key;
}
/**
* Returns the value associated with the key.
*
* @return the value associated with the key
*/
public V getValue() {
return value;
}
/**
* Replaces the value currently associated with the key with the given
* value.
*
* @return the value associated with the key before this method was
* called
*/
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
}
put(K key,V value) 添加方法添加一个节点:
public V put(K key, V value) {
Entry<K,V> t = root;
//判断根节点是否存在,如果不存在
if (t == null) {
compare(key, key); // type (and possibly null) check
// 将新的key-value对创建一个Entry,并将该Entry作为root
root = new Entry<>(key, value, null);
// 计算节点数
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
// 如果有根节点则,添加的key和root节点的key进行比较,判断是做左节点、右节点
Comparator<? super K> cpr = comparator;
// 如果比较器cpr不为null,即表明采用定制排序方式
if (cpr != null) {
//比较算法的开始,这里完成了比较和存储
do {
// 使用parent暂存上次循环后的t所对应的Entry,如果是首次则是root节点。
parent = t;
// 新插入的key和当前节点(首次是root节点)t的key进行比较
cmp = cpr.compare(key, t.key);
// 如果新插入的key的值小于t的key值,那么t=t.left即再用当前节点的左节点进行比较
if (cmp < 0)
t = t.left;
// 如果新插入的key的值大于t的key的值,那么t等于t的右节点即在用当前节点的右节点进行比较
else if (cmp > 0)
t = t.right;
else
// 如果两个key的值相等,那么新的value覆盖原有的value,并返回原有的value
return t.setValue(value);
//如果t节点的左节点、右节点不为空则继续循环!知道null为止,这样也就找到了新添加key的parent节点。
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;
do {
// 使用parent上次循环后的t所引用的Entry
parent = t;
// 拿新插入的key和t的key进行比较
cmp = k.compareTo(t.key);
// 如果新插入的key小于t的key,那么t等于t的左节点
if (cmp < 0)
t = t.left;
// 如果新插入的key大于t的key,那么t等于t的右节点
else if (cmp > 0)
t = t.right;
else
// 如果两个key相等,那么新的value覆盖原有的value,并返回原有的value
return t.setValue(value);
} while (t != null);
}
//新创建一个节点即put进来的key value
Entry<K,V> e = new Entry<>(key, value, parent);
// 如果新插入的key的值小于parent的key的值 则e作为parent的左子节点
if (cmp < 0)
parent.left = e;
// 如果新插入的key的值大于parent的key的值 则e作为parent的右子节点
else
parent.right = e;
// 修复红黑树
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
- 注意:这里没说红黑树只是说了二叉树的查找,其实TreeMap是使用红黑树的,所以有个fixAfterInsertion(e)方法(如下)就是保持红黑树的方法。参考TreeMap红黑树算法实现
<code><code><code> // 插入节点后修复红黑树
private void fixAfterInsertion(Entry<k,v> x)
{
x.color = RED;
// 直到 x 节点的父节点不是根,且 x 的父节点不是红色
while (x != null && x != root
&& x.parent.color == RED)
{
// 如果 x 的父节点是其父节点的左子节点
if (parentOf(x) == leftOf(parentOf(parentOf(x))))
{
// 获取 x 的父节点的兄弟节点
Entry<k,v> y = rightOf(parentOf(parentOf(x)));
// 如果 x 的父节点的兄弟节点是红色
if (colorOf(y) == RED)
{
// 将 x 的父节点设为黑色
setColor(parentOf(x), BLACK);
// 将 x 的父节点的兄弟节点设为黑色
setColor(y, BLACK);
// 将 x 的父节点的父节点设为红色
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
// 如果 x 的父节点的兄弟节点是黑色
else
{
// 如果 x 是其父节点的右子节点
if (x == rightOf(parentOf(x)))
{
// 将 x 的父节点设为 x
x = parentOf(x);
rotateLeft(x);
}
// 把 x 的父节点设为黑色
setColor(parentOf(x), BLACK);
// 把 x 的父节点的父节点设为红色
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
}
// 如果 x 的父节点是其父节点的右子节点
else
{
// 获取 x 的父节点的兄弟节点
Entry<k,v> y = leftOf(parentOf(parentOf(x)));
// 如果 x 的父节点的兄弟节点是红色
if (colorOf(y) == RED)
{
// 将 x 的父节点设为黑色。
setColor(parentOf(x), BLACK);
// 将 x 的父节点的兄弟节点设为黑色
setColor(y, BLACK);
// 将 x 的父节点的父节点设为红色
setColor(parentOf(parentOf(x)), RED);
// 将 x 设为 x 的父节点的节点
x = parentOf(parentOf(x));
}
// 如果 x 的父节点的兄弟节点是黑色
else
{
// 如果 x 是其父节点的左子节点
if (x == leftOf(parentOf(x)))
{
// 将 x 的父节点设为 x
x = parentOf(x);
rotateRight(x);
}
// 把 x 的父节点设为黑色
setColor(parentOf(x), BLACK);
// 把 x 的父节点的父节点设为红色
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
// 将根节点设为黑色
root.color = BLACK;
}
</k,v></k,v></k,v></code></code></code>
HashMap
HashMap类源码:
public class HashMap<K,V>extends AbstractMap<K,V>
implements Map<K,V>, Cloneable, Serializable
{
/**
* The default initial capacity - MUST be a power of two.
* 默认的容量必须为2的幂
*/
static final int DEFAULT_INITIAL_CAPACITY = 16;
/**
* The maximum capacity, used if a higher value is implicitly specified
* by either of the constructors with arguments.
* MUST be a power of two <= 1<<30.
*默认最大值
*/
static final int MAXIMUM_CAPACITY = 1 << 30;
/**
* The load factor used when none specified in constructor.
* 负载因子
*/
static final float DEFAULT_LOAD_FACTOR = 0.75f;
/**
* The table, resized as necessary. Length MUST Always be a power of two.
* 到这里就发现了,HashMap就是一个Entry[]类型的数组了。
*/
transient Entry<K,V>[] table;
HashMap类构造函数源码:
/**
* Constructs an empty <tt>HashMap</tt> with the specified initial
* capacity and load factor.
* @param initialCapacity the initial capacity
* @param loadFactor the load factor
* @throws IllegalArgumentException if the initial capacity is negative
* or the load factor is nonpositive
*/
// 初始容量(必须是2的n次幂),负载因子
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " + loadFactor);
// Find a power of 2 >= initialCapacity
int capacity = 1;
// 获取最小于initialCapacity的最大值,这个值是2的n次幂,所以我们定义初始容量的时候尽量写2的幂
while (capacity < initialCapacity)
// 使用位移计算效率更高
capacity <<= 1;
this.loadFactor = loadFactor;
//哈希表的最大容量的计算,取两个值中小的一个
threshold = (int)Math.min(capacity * loadFactor, MAXIMUM_CAPACITY + 1);
//创建容量为capacity的Entry[]类型的数组
table = new Entry[capacity];
useAltHashing = sun.misc.VM.isBooted() && (capacity >= Holder.ALTERNATIVE_HASHING_THRESHOLD);
init();
}
HashMap--put:
- 疑问思考:如果两个key通过hash%Entry[].length得到的index相同,会不会有覆盖的危险?
- 这里HashMap里面用到链式数据结构的一个概念。上面提到过Entry类里面有一个next属性,作用是指向下一个Entry。打个比方, 第一个键值对A进来,通过计算其key的hash得到的index=0,记做:Entry[0] = A。一会后又进来一个键值对B,通过计算其index也等于0,现在怎么办?HashMap会这样做:B.next = A,Entry[0] = B,如果又进来C,index也等于0,那么C.next = B,Entry[0] = C;这样我们发现index=0的地方其实存取了A,B,C三个键值对,他们通过next这个属性链接在一起。所以疑问不用担心。也就是说数组(桶)中存储的是最后插入的元素。如果hash%Entry[].length得到的index相同而且key.equals(keyother) 也相同,则这个Key对应的value会被替换成新值。
Put方法:
<span style="font-size:14px;">public V put(K key, V value) {
//key为null的entry总是放在数组的头节点上,也就是上面说的"桶"中
if (key == null)
return putForNullKey(value);
// 获取key的哈希值
int hash = hash(key);
// 通过key的哈希值和table的长度取模确定‘桶’(bucket)的位置
int i = indexFor(hash, table.length);
for (Entry<K,V> e = table[i]; e != null; e = e.next) {
Object k;
//如果key映射的entry在链表中已存在,则entry的value替换为新value
if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
modCount++;
addEntry(hash, key, value, i);
return null;
}</span>
小结:
1、HashMap 是链式数组(存储链表的数组)实现查询速度可以,而且能快速的获取key对应的value。
2、查询速度的影响因素有容量和负载因子,容量大负载因子小查询速度快但浪费空间,反之则相反。
3、数组的index值是(key 关键字, hashcode为key的哈希值, len 数组的大小):hashcode%len的值来确定,如果容量大负载因子小则index相同(index相同也就是指向了同一个桶)的概率小,链表长度小则查询速度快,反之index相同的概率大链表比较长查询速度慢。
4、对于HashMap以及其子类来说,他们是采用hash算法来决定集合中元素的存储位置,当初始化HashMap的时候系统会创建一个长度为capacity的Entry数组,这个数组里可以存储元素的位置称为桶(bucket),每一个桶都有其指定索引,系统可以根据索引快速访问该桶中存储的元素。
5、无论何时HashMap 中的每个桶都只存储一个元素(Entry 对象)。由于Entry对象可以包含一个引用变量用于指向下一个Entry,因此可能出现HashMap的桶(bucket)中只有一个Entry,但这个Entry指向另一个Entry 这样就形成了一个Entry 链。
6、通过上面的源码发现HashMap在底层将key_value对当成一个整体进行处理(Entry 对象)这个整体就是一个Entry对象,当系统决定存储HashMap中的key_value对时,完全没有考虑Entry中的value,而仅仅是根据key的hash值来决定每个Entry的存储位置。
参考HashMap、HashTable、TreeMap 深入分析及源码解析
实验总结
- 实验过程中遇到问题要及时记录;实验难度大,要参考很多资料。


