EM算法
EM算法
1.EM算法的引入
MLE极大似然估计
三硬币模型 三个硬币分别记做 A,B,C ,这些硬币正面朝上的概率分别为 \(\pi ,p,q\),首先选择抛硬币 A ,若 A 为正,则选择 B ,否则选择 C ,然后抛出所选硬币进行观测,正面记做 1 ,反面记做 0 ,重复 10 次得到如下的结果:
则:
$\pi=0.5 $
\(p=0.6\)
\(q=0.6\)
但若是隐藏硬币\(A\)的观测数据:

则三硬币模型表示为:
其中\(y\) 是观测变量,\(z\)是隐藏变量
似然函数为:
对数似然函数为:
\(P(Y|\theta)=\prod_{j=1}^n{[p^y_j(1-p)^{1-y_j}+(1-\pi)q^y_j(1-q)^{1-y_j}]}\)
求模型的极大似然估计,即:
$\hat{\theta} =arg \quad max \quad log P(Y|\theta) $
这个式子没有解析解
若是表示为方程组为:
\(\pi *p+(1-\pi)*q=0.6\)
\(\pi*(1-p)+(1-\pi)*(1-q)=0.4\)
这个方程组是没有解析解的,它的解空间有无数个解。
现给出针对以上问题的EM算法
EM算法首先选取参数的初值,记作\(\theta^0=(\pi ^0,p^0,q^0)\),然后通过下面的步骤迭代计算参数的估计值,直至收敛为止。第\(i\)次的迭代参数的估计值为\(\theta ^i = (\pi^i,p^i,q^i)\) ,\(EM\)算法的第\(i+1\)次迭代为:
E步: 计算在模型参数\(\theta ^i = (\pi^i,p^i,q^i)\)下观测数据\(y_j\)来自掷硬币B的概率
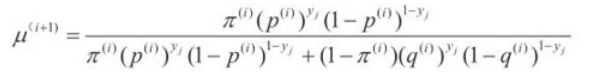
M步: 计算模型参数的新估计值
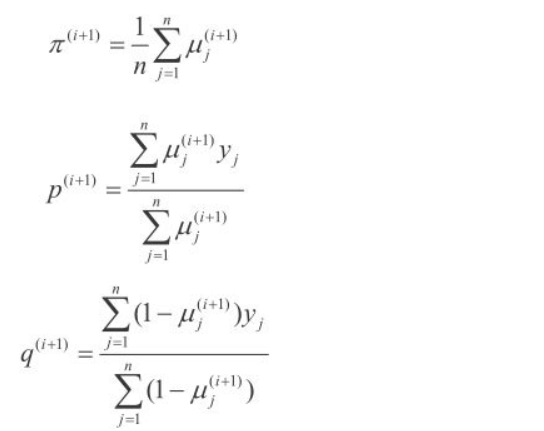
EM算法
输入:观测变量数据Y,隐变量数据Z,联合分布\(P(Y,Z|\theta)\),条件分布\(P(Z|Y,\theta)\) ;
输出:模型参数\(\theta\)
(1)选择参数的初值\(\theta ^0\),开始迭代;
(2)E步, 记\(\theta ^i\)为第i次迭代参数\(\theta\) 的估计值,在第i+1次迭代的E步,计算
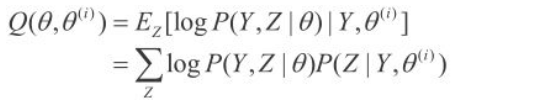
这里\(P(Z|Y,\theta ^i)\) 是在给定观测数据Y和当前的参数估计\(\theta ^i\) 下隐变量数据Z的条件概率分布;
(3)M步, 求使\(Q(\theta,\theta )\)极大化的\(\theta\),确定第i+1次迭代的参数的估计值\(\theta ^{i+1}\) 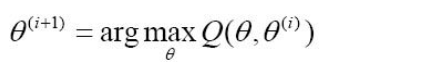
重复第(2)步和第(3)步,直到收敛。
Q函数是EM算法的核心
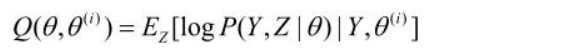
EM算法的导出
目标 极大化
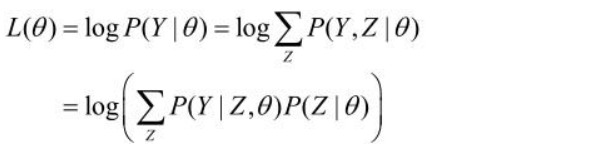
方法:迭代并使 \(L(\theta)>L(\theta ^i)\),考虑两者的差:
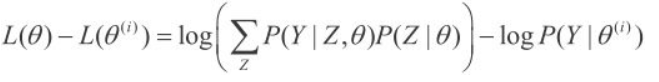
利用琴生(Jensen)不等式,得到 该式的下界:
琴生不等式:

因为\(log\)函数是凹函数,可以使用第二个不等式
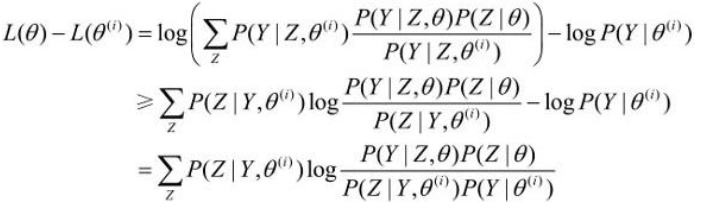
令
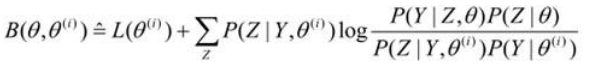
则
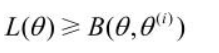
即函数\(B(\theta,\theta ^i)\)是\(L(\theta)\)的一个下界,若\(\theta = \theta ^i\),则
现求\(\theta ^{(i+1)}\) 的表达式,省去常数项\(L(\theta)\) ,得到:
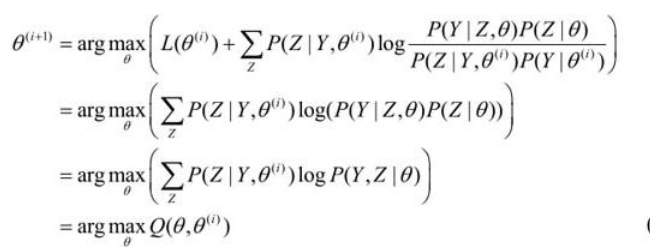
可以看出,使得\(B函数\)极大化的\(\theta\) 等价于使\(Q\)函数极大化
EM算法的直观解释,EM算法的结果可能并不是全局最优的结果
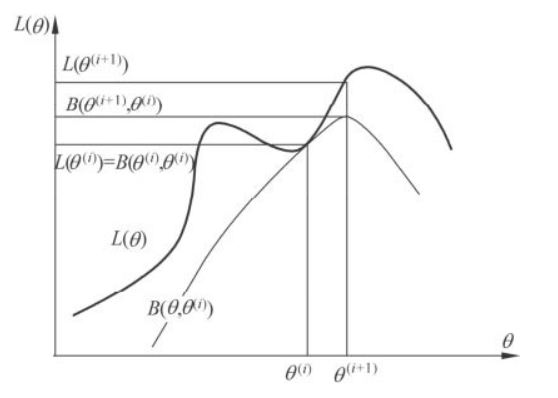
2.EM算法的收敛性
两个定理
定理1 似然函数\(P(Y|\theta ^i)\) 是单调递增的

令


定理2
- 似然函数\(L(\theta)\) 收敛
- \(\theta\) 收敛值是一稳定点
3.EM算法在高斯混合模型学习中的应用
3.1 高斯混合模型
高斯混合模型(Gaussian Mixed Model)指的是多个高斯分布函数的线性组合,理论上GMM可以拟合出任意类型的分布,通常用于解决同一集合下的数据包含多个不同的分布的情况(或者是同一类分布但参数不一样,或者是不同类型的分布,比如正态分布和伯努利分布)。
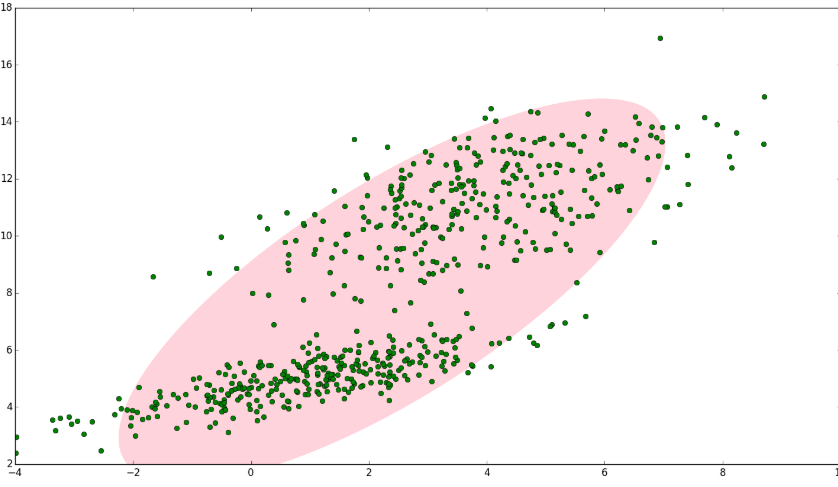
如图1,图中的点在我们看来明显分成两个聚类。这两个聚类中的点分别通过两个不同的正态分布随机生成而来。但是如果没有GMM,那么只能用一个的二维高斯分布来描述图1中的数据。图1中的椭圆即为二倍标准差的正态分布椭圆。这显然不太合理,毕竟肉眼一看就觉得应该把它们分成两类。
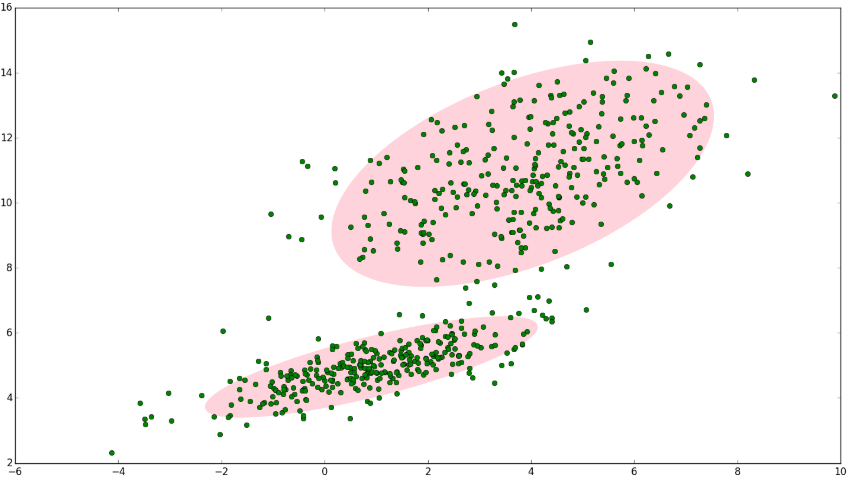
如果将两个二维高斯分布N(μ1,Σ1)N(μ1,Σ1)和N(μ2,Σ2)N(μ2,Σ2)合成一个二维的分布,那么就可以用合成后的分布来描述图2中的所有点。最直观的方法就是对这两个二维高斯分布做线性组合,用线性组合后的分布来描述整个集合中的数据。这就是高斯混合模型(GMM)。
高斯混合模型
高斯混合模型是指具有如下形式的概率分布模型:
\(P(y|\theta)=\sum_{k=1}^K \alpha ^k \phi(y|\theta_k)\)
其中\(\alpha\)是系数,\(\alpha_k\geq 0\) ,\(\sum_{k=1}^K=1\) ,\(\phi(y|\theta_k)\) 符合高斯分布,\(\theta_k=(\mu_k,\sigma_k^2)\) ,成为第\(k\)个分模型
3.2高斯混合模型参数估计的EM算法
- 确定对数似然函数


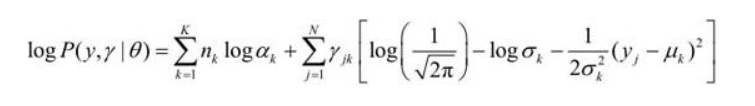
-
E步,确定\(Q\)函数
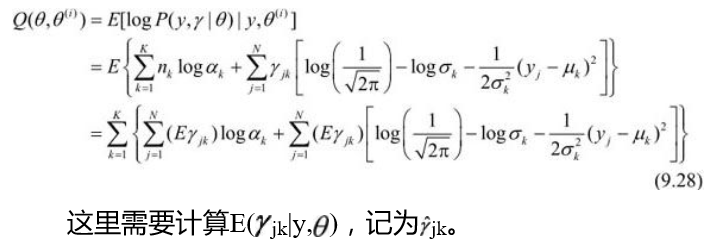

-
M步,参数迭代


