常用数学函数:
>> y = abs(x) % 取 x 的绝对值
>> y = sin(x) % 取 x 的正弦值
>> y = exp(x) % 自然指数 exp(x)
>> y = log(x) % 自然对数 ln(x)
向量矩阵的运算:
>> y = min(x) % 向量 x 的极小值
>> y = max(x) % 向量 x 的极大值
>> y = mean(x) % 向量 x 的平均值
>> y = sum(x) % 向量 x 的总和
>> y = sort(x) % 向量 x 的排序
二维平面绘图:
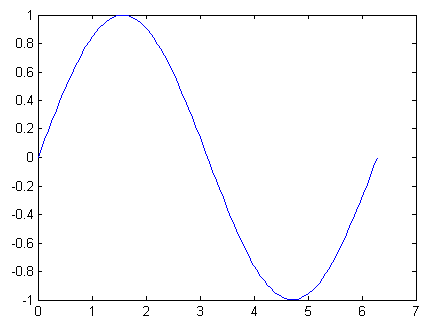
x = linspace(0, 2*pi); % 在 0 到 2π 间,等分取 100 个点
y = sin(x); %计算 x 的正弦函数值
plot(x, y); % 进行二维平面描点作图

x = linspace(0, 2*pi); % 在 0 到 2 间,等分取 100 个点
plot(x, sin(x), x, cos(x), x, sin(x)+cos(x)); % 进行多条曲线描点作图
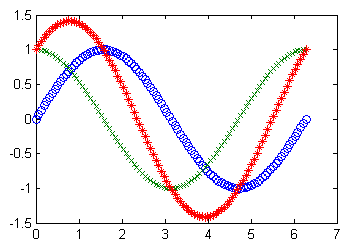
x = linspace(0, 2*pi); % 在 0 到 2 间,等分取 100 个点
plot(x, sin(x), 'o', x, cos(x), 'x', x, sin(x)+cos(x), '*');
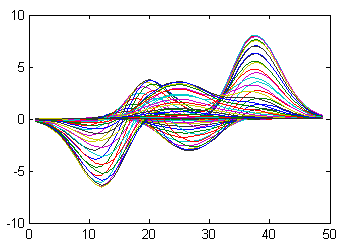
y = peaks; % 产生一个 49×49 的矩阵

plot(y); % 对矩阵 y 的每一个行向量作图

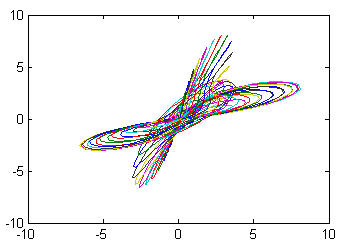
x 和 y 都是矩阵
x = peaks;
y = x'; % 求矩阵 x 的转置矩阵 x'
plot(x, y); % 取用矩阵 y 的每一行向量,与对应矩阵 x 的每一个行向量作图
提示:
一般情况下,MATLAB 将矩阵视为行向量的集合
对只能处理向量的函数(Ex : max、min、 mean) 给定一个矩阵,函数会对矩阵的行向量一一进行处理或运算

Z是一个复数向量或矩阵。
plot(z) 将 z 的实部(即 real(z))和虚部(即 imag(z))当成 x 座标和 y 座标來作图,其效果等于 plot(real(z), imag(z))
x = randn(30); % 产生 30×30 的随机数(正規分布)矩阵
z = eig(x); % 计算 x 的特征值
plot(z, 'o')
grid on % 画出网格
基本二维绘图指令
|
指令 |
说明 |
|
Plot |
x 轴和 y 轴均为线性刻度(Linear Scale) |
|
loglog |
x 轴和 y 轴均为对数刻度(Logarithmic Scale) |
|
semilogx |
x 轴为对数刻度,y 轴为线性刻度 |
|
semilogy |
x 轴为线性刻度,y 轴为对数刻度 |
|
plotyy |
画出两个刻度不同的 y 轴 |

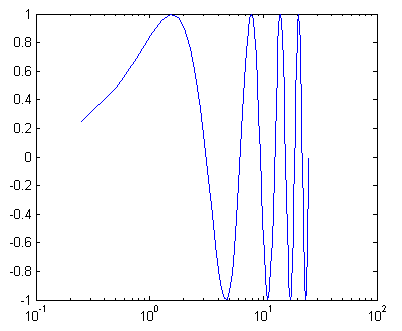
x = linspace(0, 8*pi);
semilogx(x, sin(x)); % 使 x 轴为对数刻度,并对其正弦函数作图

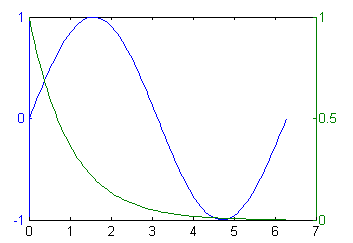
x = linspace(0, 2*pi);
y1 = sin(x);
y2 = exp(-x);
plotyy(x, y1, x, y2); % 画出两个刻度不同的 y 轴,分別是 y1, y2




